9. Числові характеристики дискретної випадкової величини.Виведення розрахункової формули дисперсії.

Числові характеристики дискретної випадкової величини:

1)Математическое ожидание

Математическим ожиданием дискретной случайной величины называется сумма произведений возможных значений на их вероятность.

М(х)= x1p1+x2p2+...+xnpn= Знак суммы(вверху n,внизу і=1) xіp;

2)дисперсия D(X)=M(X-M(X))^2

3)Среднеквадратическое отклонение сигма=

4)начальный момент

5)центральный момент

Виведення розрахункової формули дисперсії

По определению D(X)=M(X-M(X))^2 возведем двучлен стоящий под знаком дисперсии в квадрат.

D(X)=M(X-M(X))^2=M(X^2-2X M(X)+M^2(X))=M(X^2)-M(2XM(X))+M(M^2(X))=M(X^2)-2M(X) M(M(X))+M^2=M(X^2)-2M^2(X)+M^2(X)=M(X^2)-M^2(X).

10. Числові характеристики дискретної випадкової величини.Виведення розрахункової формули дисперсії.

Числові характеристики дискретної випадкової величини:

1)Математическое ожидание

Математическим ожиданием дискретной случайной величины называется сумма произведений возможных значений на их вероятность.

М(х)= x1p1+x2p2+...+xnpn= Знак суммы(вверху n,внизу і=1) xіp;

2)дисперсия D(X)=M(X-M(X))^2

3)Среднеквадратическое отклонение сигма=

4)начальный момент

5)центральный момент

ПОСТОЯННЫЙ МНОЖИТЕЛЬ можно вывести за знак дисперсии возведя его в квадрат

11.Числовые характеристики дискретной случайной величины.

Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение.

Характеристикой среднего значения случайной величины служит математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой постоянной: 

2. Постоянный  можно выносить за знак математического ожидания:

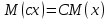
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:

4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:

(для разности аналогично)

Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.

Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X)=M(X-M(X))^2

Дисперсию удобно вычислять по формуле: D(X)=M(X^2)-(M(X))^2

Свойства дисперсии:

1. Дисперсия постоянной равна нулю:D(C)=0

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:D(cx)=D(x)

3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:

4. Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:

Сигма(х)=

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a _k = Mx ^k.

Центральным моментом k-го порядка случайной величины x называется величина m _k, определяемая формулой m _k = M(x - Mx )^k.

12. Вивід розрахункових формул центральних моментів через початкові.

Центральным моментом порядка k дискретной случайной величины называют математическое ожидание отклонения в степени 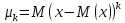k : . Начальный момент порядка k дискретной случайной величины называют математическое ожидание случайной величины степени k: . Например: .

13.непрерывная случайная величина. Функцией распределения непрерывной случайной величины называется функция F(x) равная вероятности того,что случайная величина во время испытания примет значения меньше своего любого возможного значения. F(x)=P(X-x)

Свойства:

1.ф-я распределения всегда лежит в интервале от 1 до 0.

2.ф-я распределения неубываемая ф-я F(x2)>=F(x1) при x2>=x1.

3.вероятность того, что случайная величина примет значение заключенное в интервале (а,в) равна приращиванию функции распределения на этом интервале

P(a<=x<=b) = F(b)-F(a)

4.если возможные значения непрерываной случайной величины расположены на всей оси х то справедливы след предельные соотношения (lim f(x)=0 (x->- безконечности), lim f(x)=1 (x-> +безконечности)

Функция распределения, является переходной характеристикой между дискретной и непрерывной случайной величинами. Ф-я распределения как для дискретной так и для случайной величиы. Для дискретной случ величины, ф-я распределения представляет из себя ступенчатую ф-ю.

14. Густиною (щільністю) імовірностей неперервної випадкової величини Х є перша похідна від інтегральної функції розподілу ймовірностей f(x): f(x)=F’(x)

Плотность распределения существует только для непрерывной случайной величины.

Свойства:

1.вероятность того,что непрерывная случайная величина х примет значение пренадлежащее интервалу (а,в) равно определенному инегралу от плотности распределения взятому в пределах от а до в

2. плотность распределения неотрицательная функция f(x)>=0

3.несобственный интеграл от плотности распределения в пределах(-бескон;+бескон) равен 1dx=1

15) Числовые характеристики НСВ 1-математическое ожидание 2-дисперсия

3- среднеквадратическое отклонение )

4 начальный момент

5. центральный момент порядка к(вывести расчетную формулу центрального момента через начальный,а затем все начальные моменты записать по формулам для непрерывной случайной величины)

+-+