1. Елементи комбінаторики. Основні формули комбінаторики. Біном Н’ютона.

Основные формулы комбинаторики: а) перестановка: Pn=n!=n(n-1)(n-2)*…*1; б) Размещение: ; в) Сочетания: ; г) Бином Ньютона :

Бином Ньютона: 1)в разложении n-степени бинома содержится (n+1) слагаемых; 2) Разложение бинома – однородный многочлен, относительно a и b, при этом показатели a последовательно убывают от n до 0, а показатели b последовательно возрастают от 0 до n; 3) формула любого члена бинома 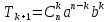; 4) биномиальные коэффициенты, равноотстоящие от концов разложения равны между собой ; 5) Если показатель степени бинома четный, то биномиальный коэффициент среднего слагаемого разложения наибольший; если степень нечетная, то в разложении имеется 2 средних слагаемых с одинаковым наибольшим коэффициентом; 6) Сумма всех биномиальных коэффициентов равна , где n – показатель бинома; 7) Сумма биномиальных коэффициентов, стоящих на четных местах равно сумме коэффициентов, стоящих на нечетных местах.

2.

Класичною ймовірністю події А називається відношення числа сприятливих появі події результатів до загального числа всіх можливих елементарних результатів випробування

При статистичному означенні в якості ймовірності події приймають її відносну частоту, де m - число випробувань, в яких подія відбулася, п - загальне число

проведених випробувань.

Вірогідною (достовірною) називається подія , яка внаслідок випробування неодмінно повинна статися. Для достовірної події ймовірність рівна одиниці P(U)=1. Неможливою називається подія , яка внаслідок досвіду не може відбутися. Для неможливої події ймовірність рівна нулю P ( )=0 . Несумісними називаються події А і В які не можуть відбутися

3) ТЕОРЕМЫ СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Теорема 1: вероятность суммы несовместных событий равно сумме вероятностей этих событий

Доказательство:

Введем обозначение: пусть n-общее число исходов, m1-число исходов благоприятствующих собітию А. m2-число исходов благоприятствующис событию В. Тогда число благоприятствующих исходов появления либо события А либо события В равно А+В  m1+m2 по определению действие над событиями.

По классическому определению вероятности:

Теорема доказана.

Теорема 2: сумма вероятностей событий образующих полную группу равно 1.

Доказательство:

По определению событий полной группы в результате испытания одно из них обязательно произойдет следовательно это достоверное событие, а по первому свойству вероятности – вероятность достоверного события равно 1.

Теорема3:сумма вероятностей противоположных событий равна 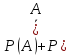1: =1

Доказательство: по определению противоположных событий они образуют полную группу, а по теореме 2 сумма вероятностей этих событии равна единице.

ТЕОРЕМЫ УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ :

Независимые события: вероятность совместного появления двух независимых событий равно произведению вероятностей этих событий

Зависимые события: вероятность совместного появления двух зависимых событий равно произведению вероятности одного из них на условную вероятность другого 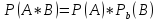вероятность обытия А называется условная в том случае если событие А настает в том случае если произошло событие В.

Формула полной вероятности: Пусть событие А наступит в том случае если произойдет одно из событий В,В1,В2,….,Вн , образующих посную группу , тога вероятность события А можно посчитать по формуле полной вероятности

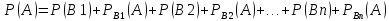
Формула Бейеса

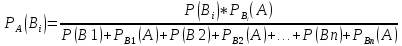
4.Вероятность гипотез

Т.Бернулли: Если производится испытание при которыз вероятность появления события А в каждом испытании независит отот исхода других испытаний то вероятность такого события вычисляется по формуле Бернулли 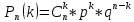где q = 1 – p. Вероятность того что в н испытаниях событие наступит: 1)менее к раз:; 2)более к раз:; 3)не менее к раз :; не более к раз: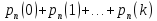

5.Дискретні випадкові величини. Розуміння про закон та функції розподілу ймовірності дискретних випадкових величин. Дискретной случайной величиной называется случайная величина которая принимает отдельные изолированные возможные значения с определением вероятности. Законом распределения дискр.случайной величины называется соответствие между возможными значениями этой величины и их вероятностями.

Х ...

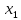
P ...

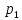
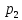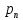
Случайная величина может быть заданна графически, аналитически и таблично.Возможные значения образуют полную группу событий, а по Теореме 2 сумма вероятностей этих событий равна 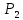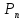1.

++...+=1

6.Числовые характеристики дискретных случайных величин

1)Математическое ожидание-сумма произведений возмодных значений на их вероятности.

М(X)=Х1P1+X2P2+…+XnPn

Свойства:-математическое ожидание постоянной равно самой постоянной М(С)=С; -постоянный множитель можно выносить за знак математического ожидания М(СХ)=СМ(Х); -математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий М(Х+У)=М(Х)+М(У); -математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий М(Х*У)=М(Х)*М(У)

2)Дисперсия-математическое ожидание квадрата отклонения случайной величины от своего среднего значения. Д(Х)=М(Х-М(Х))². Свойства:

-математическое ожидание отклонения равно нулю ; -постоянный множитель можно выносить за знак дисперсии Д(СХ)=С²М(Х); -дисперсия суммы двух случайных величин равно сумме их дисперсий Д(Х+У)=Д(Х)+Д(У); - дисперсия разности двух случайных величин равно сумме их дисперсий Д(Х+У)=Д(Х)+Д(У); 3)Среднее квадратическое отклонение σ=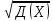;4)Начальный момент порядка к V_k=M (X^K);5)Центральный момент порядка к µ_k=M(X-M(X))^K;

7. Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D ( X ) = M ( X - M ( X )) 2.Свойства: 1.Математическое ожидание отклонения=0. М(х-М(х))=М(х)-М(М(х))=М(х)-М(х)=0 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат : D ( сх ) = М(сх-М(сх)) 2 =М(сх-СМ(х)) 2 =М(с(х-М(х))) 2 =М(с2 (х-М(х)) 2 )=с2 М(х-М(х)) 2 =C 2D (х). 3. Дисперсия суммы случайных величин равна сумме их дисперсий: D ( X+Y ) = D ( X )+D ( Y ) 4. Дисперсия разности 2-х случ величин равна сумме их дисперсий D(x-y)=D(x)+D(-y)=D(x)+D((-1)*y)=D(x)+(-1) 2 D(y)=D(x)+D(y) ; Расчетная формула дисперсии D ( X ) = M ( X - M ( X )) 2=М (х2-2хМ(х)+М2(х))=М(х2) –М(2х*М(х))+М(М2 (х))=М(х2) -2М(х)*(М(х))+М2 (х)=М(х2 )-2М2 (х)=М(х2 )-М2 (х); Дисперсия равна разности математического ожидания квадратов случайной величины и квадрат её математического ожидания.

8. Дискретная случайная величина – дискретной случ. Величиной называется величина, которая принимает отдельные, изолированные значения с определенными вероятностями^. Дисперсия – дискретная случ. Величина наз. Мат. Ожидание квадрата отклонения случ. Величины от своего среднего значения. D(x)=M(x-M(x))^2^. .вывод формулы разности дисперсий: D(x-y)=D(x)+D(-y)=D(x)+D((-1)*y)=D(x)+(-1)^2*D(x)=D(x)+D(y)