
Решение
1. Доверительные границы случайной составляющей:
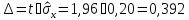 мА (14.1)
мА (14.1)
Где
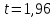 - коэффициент Стьюдента при количестве
измерений
- коэффициент Стьюдента при количестве
измерений
 .
.
2. Определяем доверительные границы неисключенной систематической погрешности результата измерения
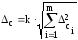 (14.2)
(14.2)
где m - число суммируемых погрешностей;
 -
граница i-й неисключенной систематической
погрешности;
-
граница i-й неисключенной систематической
погрешности;
k - коэффициент, определяемый принятой доверительной вероятностью.
При доверительной вероятности Рд = 0,95 коэффициент k принимают равным 1,1.
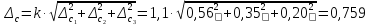 мА
(14.3)
мА
(14.3)
3. Определим границы суммарной погрешности результата измерения.
а) Находим отношение:
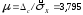 (14.4)
(14.4)
б)
В случае если
< 0,8, то неисключенными систематическими
погрешностями по сравнению со случайными
пренебрегают и принимают, что граница
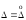 .
Если
> 8, то пренебрегают случайной погрешностью
по сравнению с систематическими и
принимают, что граница погрешности
результата
= с.
.
Если
> 8, то пренебрегают случайной погрешностью
по сравнению с систематическими и
принимают, что граница погрешности
результата
= с.
Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанныx неравенств, не превышает 15 %.
в) В случае, если неравенства п. б) не выполняются (0,8 8), то границу погрешности результата измерения находят путём построения композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины.
4. Определим границы суммарной погрешности результата измерения.
Границы погрешности результата измерения (без учета знака) вычисляют по формуле
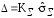 (14.5)
(14.5)
где К- коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
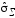 -
оценка суммарного среднего квадратического
отклонения результата измерения.
-
оценка суммарного среднего квадратического
отклонения результата измерения.
Значение
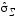 вычисляют по формуле
вычисляют по формуле
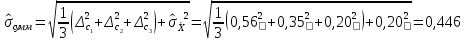 мА
(14.6)
мА
(14.6)
Коэффициент К вычисляют по эмпирической формуле
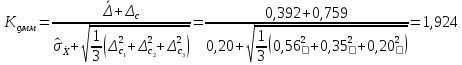 (14.7)
(14.7)
Определяем доверительные границы суммарной погрешности результата измерения
|
|
|
5. Записываем результат измерения. Так как погрешность симметрична относительно результата измерения, то
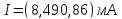 ,
Рд
= 0,95 (14.9)
,
Рд
= 0,95 (14.9)
Ответ:
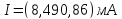 ,
Рд
= 0,95.
,
Рд
= 0,95.
N18/4
Сопротивление
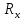 определялось косвенным методом путём
многократных измерений (n=19) падения
напряжения на нём
определялось косвенным методом путём
многократных измерений (n=19) падения
напряжения на нём
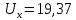 B
и падения напряжения
B
и падения напряжения
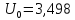 B
на последовательно соединенным с ним
образцовом резисторе
B
на последовательно соединенным с ним
образцовом резисторе
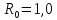 кОм с последующим расчётом
кОм с последующим расчётом
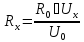 .
Оценки средних квадратических отклонений
среднего арифметического
.
Оценки средних квадратических отклонений
среднего арифметического
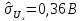 ,
,
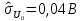 ,
оценка коэффициента корреляции между
погрешностями измерений
,
оценка коэффициента корреляции между
погрешностями измерений
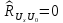 .
.
Определить случайную погрешность результата косвенного измерения с доверительной вероятностью Рд = 0,95 и записать результат по одной из установленных форм.
Решение
1. Находим значение результата косвенного измерения напряжения
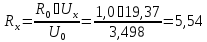 кОм
(18.1)
кОм
(18.1)
2. Определяем частные случайные погрешности косвенного измерения
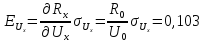 кОм;
(18.2)
кОм;
(18.2)
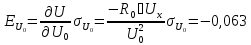 кОм; (18.3)
кОм; (18.3)
3. Вычисляем оценку среднего квадратического отклонения результата косвенного измерения:
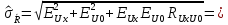
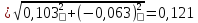 кОм (18.4)
кОм (18.4)
4. Определяем значение коэффициента Стьюдента t для заданной до-верительной вероятности Рд и числа наблюдений n.
При n 30 предварительно должно быть определено так называемое «эффективное» число степеней свободы распределения Стьюдента,
Оно определяется из выражения
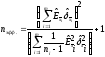 ,
(18.5)
,
(18.5)
где ni - число наблюдений при прямых измерениях xi .
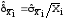 - относительная оценка среднеквадратического
отклонения
- относительная оценка среднеквадратического
отклонения
Для
решаемой задачи
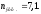
в) При получении дробного значения nэфф для нахождения коэффициента Стьюдента применяем линейную интерполяцию:
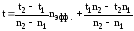 ,
(18.6)
,
(18.6)
где t1, t2 и n1, n2 - соответствующие табличные значения коэффициента Стьюдента и числа наблюдений (для заданной Рд), между которыми находится значение nэфф.
Для решаемой задачи при nэфф =7,1 и Рд = 0,95 находим n1 = 7,
t1 = 2,365, n2 = 8, t2 = 2,306, а затем вычисляем значение t = 2,36.
5. Вычисляем доверительные границы случайной погрешности результата косвенного измерения:
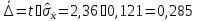 кОм (18.7)
кОм (18.7)
6. Записываем результат измерения:
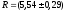 кОм Рд=0,95.
(18.8)
кОм Рд=0,95.
(18.8)
7. Проанализируем полученные результаты с использованием критерия ничтожных погрешностей.
В соответствии с этим критерием, если частная погрешность меньше 1/3 суммарной погрешности, то она является «ничтожной» и может быть исключена из рассмотрения.
Для
решаемой задачи

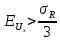 ;
;
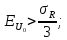
Следовательно
частные погрешности
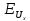 и
и
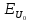 не
считаются «ничтожными», и ими нельзя
пренебречь.
не
считаются «ничтожными», и ими нельзя
пренебречь.
Ответ:
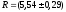 кОм Рд=0,95.
кОм Рд=0,95.
N24/3
На
основе МЭИМ с внутренним сопротивлением
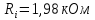 ,
ценой деления
,
ценой деления
 и шкалой с
и шкалой с
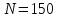 делениями
необходимо создать вольтамперметр с
пределами измерения по току
делениями
необходимо создать вольтамперметр с
пределами измерения по току
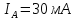 ,
по напряжению
,
по напряжению
 .
Рассчитать сопротивление шунта и
добавочного резистора, определить цену
деления по току
.
Рассчитать сопротивление шунта и
добавочного резистора, определить цену
деления по току
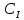 и по напряжению
и по напряжению
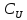 ,
начертить принципиальную схему
вольтамперметра.
,
начертить принципиальную схему
вольтамперметра.

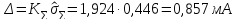
 (14.8)
(14.8)