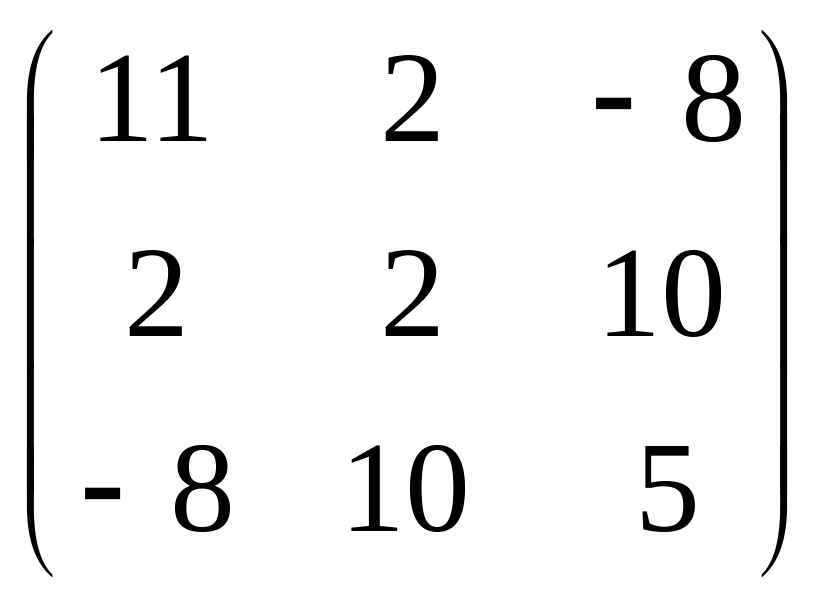Задачи для контроля изученного материала
|
Формулировка задачи |
1 вариант |
2 вариант |
1 |
Найти собственные векторы и собственные значения линейного оператора, действующего в евклидовом пространстве и имеющего в ортонормированном базисе e1, e2, e3 матрицу. Составить матрицу из собственных значений |
|
|
2 |
Найти матрицу сопряженного оператора A* в базисе f1, f2; e1, e2 - ортонормированный базис, если дана матрица линейного оператора A евклидова пространства в базисе f1, f2 . |
базисе f1= e1+ e2, f2=e2 |
базисе f1= e1, f2=e1+ e2 |
Ответы. 1.
Поворот на
угол - ,
,
в базисе i , j.
2.
Нуль-оператор,
.
3.
Тождественный
оператор,
.
4.
Оператора подобия
.
5.
Являются все
самосопряженными, кроме оператора
поворота, на углы не кратные .
6.
A*
f = Af
= - f(x).
7.
не являются
самосопряженными.
7.
.
8.
1) 1=1,
(3,-5,4), 2=-4,
(-4,0,3), 3=6,
(3,5,4),
;
2) 1=-1,
(1,-2,1), 2=1,
(2,1,0),
(-1,2,5),
;
3) 1=9,
(1,1,0), 2=18,
(1,-1,4), 3=27,
(-2,-2,1),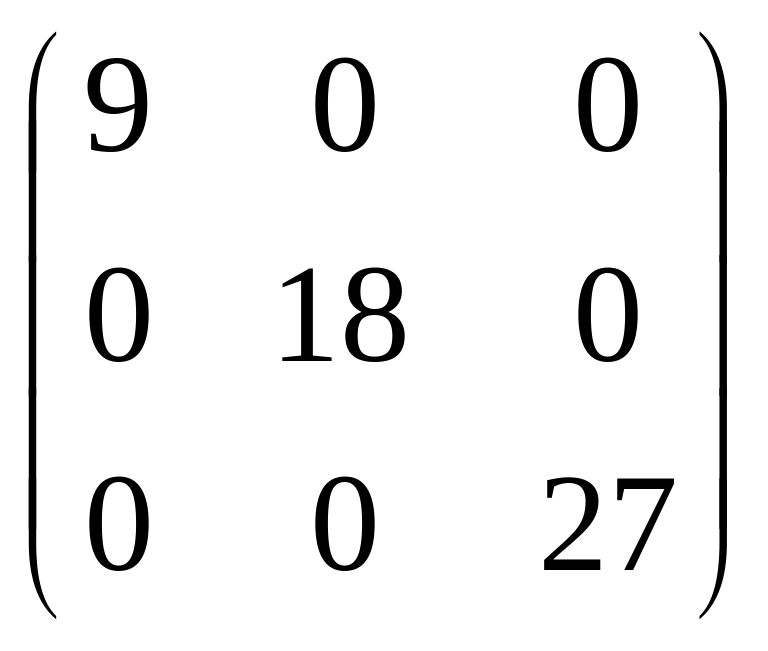
;
4) 1=9,
(2,2,1), 2=18,
(2,-1,2), 3=-9,
(1,-2,2),
.
9.
10.
Ортогональный.
Дома. Билинейные и квадратичные формы.