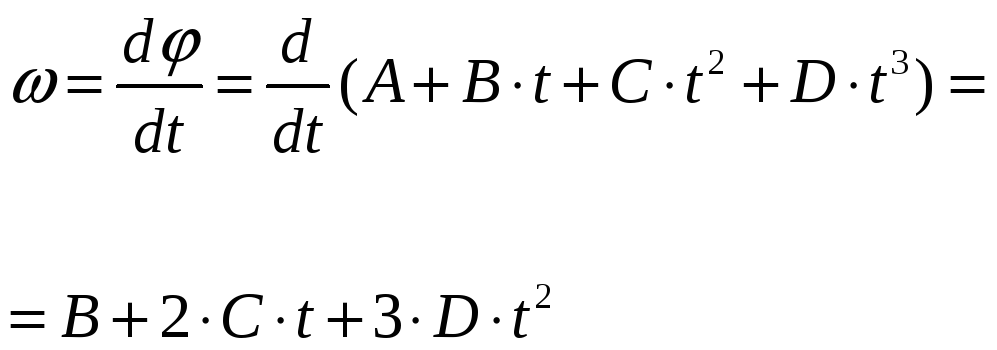Контрольная механика
.docЗадача № 107
Колесо вращается
так, что зависимость угла поворота
радиуса колеса от времени имеет вид:
,
где
,
,
.
Найдите радиус колеса, если известно,
что к концу второй секунды движения для
точек, лежащих на ободе колеса, нормальное
ускорение
|
Дано:
|
Решение: Угловая скорость материальной точки, движущейся по окружности:
Линейная скорость связана с угловой соотношением: |
|
Найти: R - ?
|
,
где R- радиус окружности.
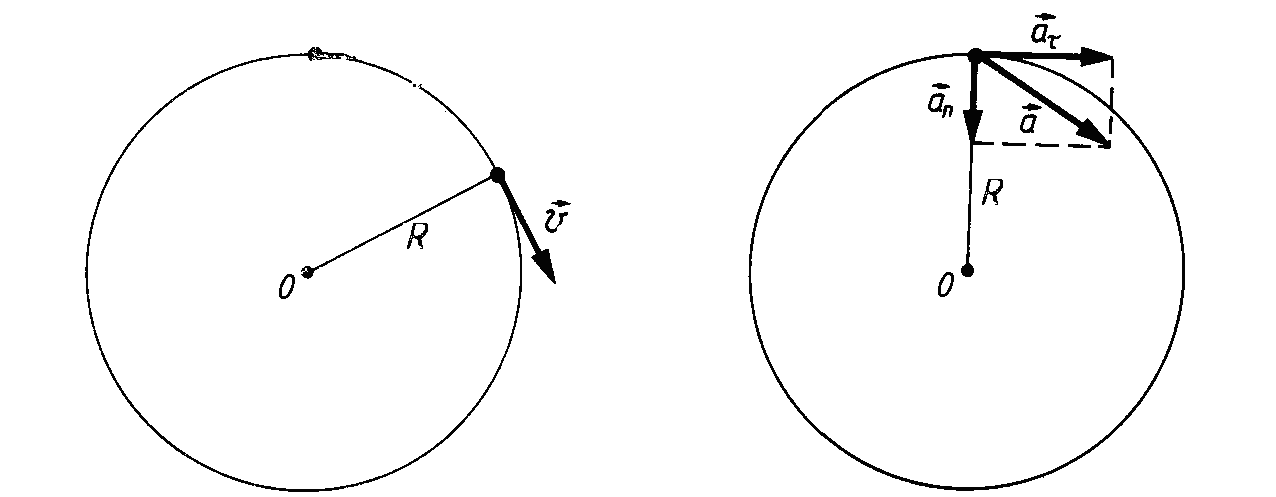
Нормальное ускорение определяется по соотношению:
Значит:
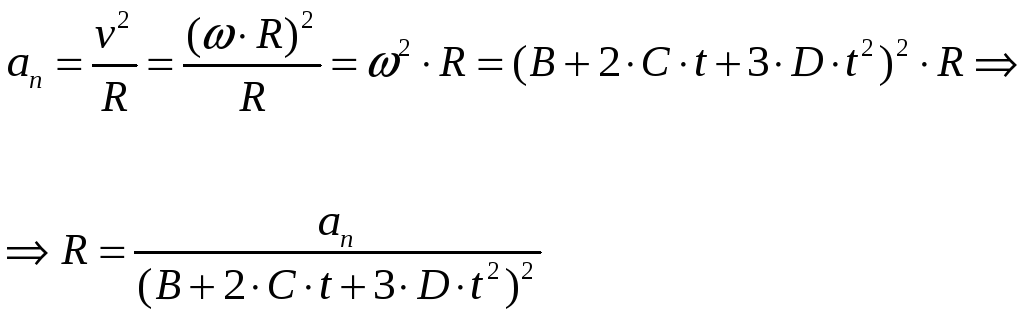
Проводим анализ размерности:
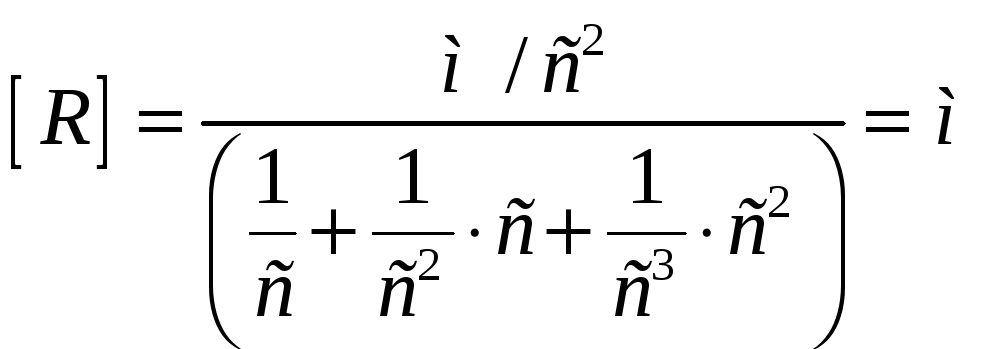
Проводим расчёт:
Ответ:
Задача № 117
Два тела массой m = 100 г каждое подвешены на краях нити, перекинутой через блок. На одно из тел положен перегрузок массой m0 = 50 г. С какой силой он будет давить на тело, на котором лежит, когда вся система придёт в движение.
|
Дано: m = 100 г=0,1 кг m0 = 50 г = 0,05 кг g = 9,8 м/с2
|
Решение: Изображаем на рисунке все силы, действующие на тела. Направляем ось Ox вниз и составляем уравнения II-го закона Ньютона для всех трёх тел.
|
|
Найти:
|
- ?
Сила
-
это сила, с которой тело
действует
на перегрузок
.
А сила
- это сила, с которой перегрузок
действует на тело
.
По третьему закону Ньютона
.
Решаем систему из трёх уравнений:
Анализ размерности:
Проводим расчёт:
Ответ:
Задача № 127
Винтовка массой
3 кг подвешена горизонтально на двух
параллельных нитях. При выстреле в
результате отдачи она поднялась на
вверх на
=19,6
см. Масса пули
=10
г. Определите скорость, с которой вылетела
пуля.
|
Дано:
|
Решение:
|
|
Найти:
|
=3
кг
=19,6
см = 0,196 м
=10
г = 0,01 кг
Ответ:
Задача № 137
Работая с постоянной
мощностью, локомотив может тянуть поезд
вверх по склону при угле наклона
со скоростью
.
При угле наклона
при тех же условиях он развивает скорость
.
Определите коэффициент трения, считая
его одинаковым в обоих случаях.
|
Дано:
|
Решение:
|
|
Найти:
|
Ответ:
Вдоль стального
стержня, плотность которого
распространяется продольная упругая
волна со скоростью
.
Амплитуда колебаний равна 1 мкм, длина
волны
.
Определить максимальное значение
плотности потока энергии (с выводом
формулы).
|
Дано:
|
Решение: Максимальное значение плотности потока энергии (интенсивность волны) определяется средней энергией, переносимой волной в единицу времени через площадку единичной площади, установленную перпендикулярно к направлению распространения волны.
|
|
Найти:
|
(1)
Определяем энергию, переносимую волной. Для этого выделяем в упругой среде, в которой распространяется волна, некоторый объём V.
vdt
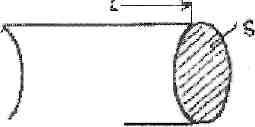
Избыточная энергия этого объёма:
,
где
-
кинетическая энергия элементов среды;
- потенциальная энергия упруго
деформированного объёма.
Так как
Уравнение плоской монохроматической волны возьмём в виде:
Потенциальная энергия упруго деформированного объема равна:
Где
- относительная деформация среды;
- модуль Юнга; V
– выделенный объём.
Так как:
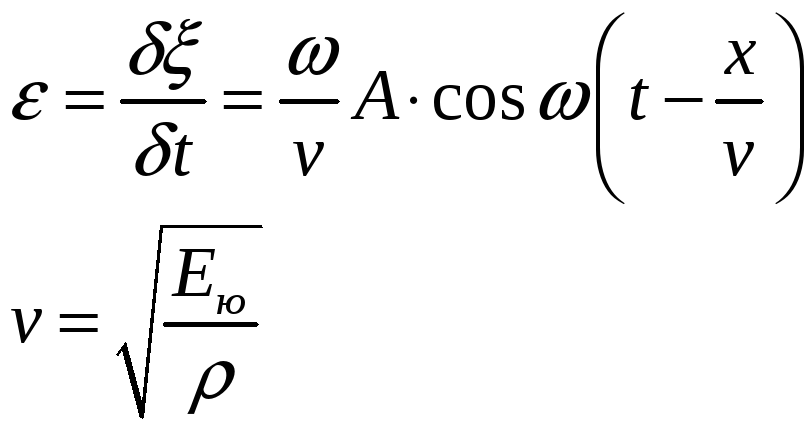
Получаем:
Полная энергия выделенного объёма:
Максимальное
значение плотности потока энергии будет
при максимальном значении
Если взять отношение энергии к объему, то получим объемную плотность:
т.е. объемная плотность энергии выделенного объема определяется величинами, характеризующими волновой процесс. Таким образом, можно сделать вывод о том, что волна переносит энергию, средняя объемная плотность которой определяется последней формулой.
Интенсивность волны связана со средней объемной плотностью энергии соотношением (вектор Умова):
Следовательно, максимальное значение плотности потока энергии равно:
Расчёт:
Для данной волны имеем:
Ответ:
