
Контрольная работа 1 курс 2 семестр (20 вариант)
.docxЗадача №110
Уравнение
скорости точки имеет вид
 Найти
зависимость пути от времени и вычислить
путь за первые 3 с.
Найти
зависимость пути от времени и вычислить
путь за первые 3 с.
Дано: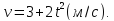
Найти: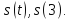
Решение:
Найдем зависимость пути от времени путем интегрирования уравнения скорости по времени:
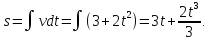
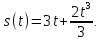
Определим путь, пройденный за первые три секунды:

Ответ:

Задача №120.
Парусник массой 3 т двигается прямолинейно под действием постоянной силы ветра, а пройденный путь равен S = (5+3t+t2) м. Найти работу силы ветра за время от 3 до 5 с.
Дано:
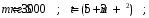 .
.
Найти: А(5с-3с).
Решение.
Путь, пройденный телом, выражается следующей формулой:

Приравнивая данное выражение к исходному выражению, находим значение начального перемещения, скорости и ускорения:
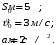
Работа силы ветра находится как произведение силы ветра на пройденный телом путь, под действием данной силы:

Величина ускорения и массы парусника нам уже известны, осталось найти путь, который парусник пройдет с 3-ей по 5-ую секунду, для этого подставим в формулу пути время, а затем от одного значения при 5 секундах отнимем второе, при 3 секундах.
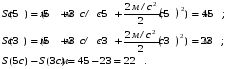
Подставим значения в системе СИ и найдем значение работы:
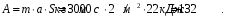
Ответ:

Задача №130
Колесо
диаметром
 и массой
и массой
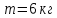 ,
равномерно распределенной по ободу,
вращается с частотой
,
равномерно распределенной по ободу,
вращается с частотой
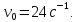 Какой момент силы надо приложить к
колесу, чтобы его остановить за
Какой момент силы надо приложить к
колесу, чтобы его остановить за
 .
.
Дано:

Найти: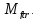
Решение:

Из
второго закона Ньютона применяемого к
вращающимся телам, находим:
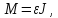 где M-
момент сил,
где M-
момент сил,
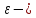 угловое
ускорение, J
– момент инерции диска. Момент инерции
однородного диска массой m
и радиусом К равен
угловое
ускорение, J
– момент инерции диска. Момент инерции
однородного диска массой m
и радиусом К равен
 Поэтому
Поэтому
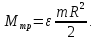
Зависимость
угловой скорости при равнозамедленном
вращении записывается в виде
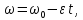 где
где
 начальная
угловая скорость.
начальная
угловая скорость.
Известно,
что через время
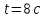 диск остановился и
диск остановился и
 Поэтому
Поэтому

Откуда
угловое ускорение равно
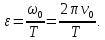 Подставляем в
Подставляем в
 и получаем:
и получаем:
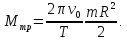
Так
как радиус
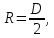 то
то

Подставляем числа (переводя все величины в систему СИ):
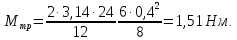
Ответ:
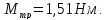
Задача №140.
По горизонтальной плоскости катится шар с начальной скоростью 10 м/с; пройдя путь 20 м, он остановился. Найти коэффициент сопротивления и кинетическую энергию в середине пути.
Дано:
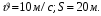 .
.
Найти:
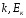 .
.
Решение.

Так как шар катится,
а не скользит, т о он будет вращаться с
угловой скоростью
 и двигаться поступательно со скоростью
и двигаться поступательно со скоростью
 .
.
Угловые и линейные величины, характеризующие движение точки по окружности (в нашем случае на поверхности шара ) связаны соотношением :

, где R-
радиус шара. Поэтому
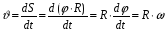 . Откуда
. Откуда
 .
.
По определению кинетическая энергия вращения равна:
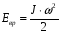
, где
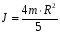 -момент
инерции сплошного шара. Тогда
-момент
инерции сплошного шара. Тогда
 ,
а так как
,
а так как
 , то
, то
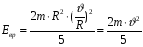 .
.
Помимо вращения
существует поступательное движение со
скоростью
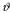 .
По определению кинетическая энергия
поступательного движения
.
По определению кинетическая энергия
поступательного движения
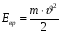 .
.
Тогда полная кинетическая энергия равна:

Когда шар катится,
на него действует сила трения, равная
 , где k-
коэффициент сопротивления. Работа сил
трения равна
, где k-
коэффициент сопротивления. Работа сил
трения равна
 , где S-
пройденный путь. Так как диск остановился,
то вся кинетическая энергия пошла на
работу сил трения:
, где S-
пройденный путь. Так как диск остановился,
то вся кинетическая энергия пошла на
работу сил трения:
 . Поэтому
. Поэтому
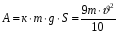 , откуда искомая величина равна:
, откуда искомая величина равна:

Кинетическая энергия шара в середине пути равна половине полной кинетической энергии в начале движения, так как работа силы трения будет в два раза меньше полной:
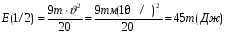
Ответ:
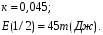
Задача №150
Опредлить период гармонических колебаний диска радиусом 40 см около горизонтальной оси, проходящей через образующую диска.
Дано: R=40 см .
Найти:Т.
Решение.
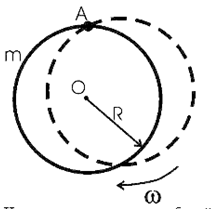
Известно что период колебаний физического маятника равен:
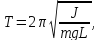
где J – момент инерции тела относительно точки подвеса; m – масса физического маятника; L – расстояние от точки подвеса до центра тяжести маятника (L=R).
Для нашего случая нужно найти момент инерции диска J относительно точки подвеса А. Для того чтобы вычислить момент инерции диска в точке А воспользуемся теоремой Штейнера:
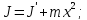
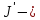 момент инерции
тела относительно его оси симметрии.
момент инерции
тела относительно его оси симметрии.
В нашем
случае x=R,
а
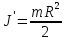 – момент инерции диска относительно
его оси симметрии, поэтому
– момент инерции диска относительно
его оси симметрии, поэтому
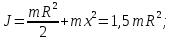
Тогда

Подставляем числа (преводя одновременно все величины в систему СИ).
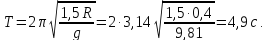
Ответ:
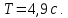
Задача №160.
Определить среднюю кинетическую энергию поступательного и вращательного движения молекулы азота при температуре Т = 1 кК. Определить также полную кинетическую энергию молекулы при тех же условиях.
Дано:
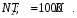 .
.
Найти:
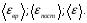 .
.
Решение.
Средняя кинетическая
энергия поступательного движения одной
молекулы равна
 , где
, где
 -постоянная Больцмана, i-
поступательные степени свободы (i=3
в нашем случае, так как три поступательных
движения возможны). Подставляем числа:
-постоянная Больцмана, i-
поступательные степени свободы (i=3
в нашем случае, так как три поступательных
движения возможны). Подставляем числа:
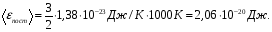
Средняя кинетическая
энергия вращательного движения одной
молекулы равна
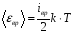 , где iвр
–степени свободы молекулы(iвр
=2, так как молекула двухатомная). Поэтому
, где iвр
–степени свободы молекулы(iвр
=2, так как молекула двухатомная). Поэтому
 . Подставляем числа в системе СИ:
. Подставляем числа в системе СИ:

Полная энергия поступательного движения одной молекулы равна сумме поступательной и вращательной:

Ответ:
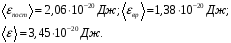
Задача №170
Определить работу, которую совершит азот, если ему при постоянном давлении сообщить количество теплоты Q=21 кДж. Найти также изменение внутренней энергии газа.
Дано: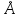 ,
,
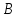
Найти: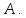
Решение:
При изобарическом процессе количество затраченной энергии на нагрев азота:
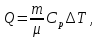 где
где
 –масса азота,
–масса азота,
 малярная
масса азота,
малярная
масса азота,
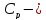 малярная
изобарная теплоемкость азота. Молярная
изобарная теплоемкость вычисляется по
формуле
малярная
изобарная теплоемкость азота. Молярная
изобарная теплоемкость вычисляется по
формуле

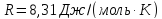 - молярная газовая
постоянная, i
–число степеней свободы молекулы азота
( для азота 3 поступательные и 2 вращательные
i=5).
Поэтому
- молярная газовая
постоянная, i
–число степеней свободы молекулы азота
( для азота 3 поступательные и 2 вращательные
i=5).
Поэтому

По определениюизменение внутренней энергии газа равно

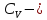 молярная
изохорная теплоемкость азота. Выражаем
изменение внутренней энергии через Q:
молярная
изохорная теплоемкость азота. Выражаем
изменение внутренней энергии через Q:

Молярная изохорная теплоемкость вычисляется по формуле

i- число степеней свободы молекулы. Поэтому
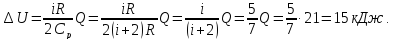
Применим
первый закон термодинамики. Согласно
которому, количество теплоты Q,
переданное системы, расходуется на
увеличение внутренней энергии
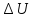 и на внешнюю механическую работу A:
Q=
и на внешнюю механическую работу A:
Q= Откуда
Откуда

Ответ:

Задача №180.
В цикле Карно газ получил от теплоотдатчика теплоту Q1= 500 Дж и совершил работу А = 100 Дж. Температура теплоотдатчика Т1=400 К. Определить температуру Т2 теплоприемника.
Дано:
 .
.
Найти:Т2.
Решение.
КПД тепловой машины равен отношению производимой работы А к количеству тепла Q1, полученному рабочим телом от нагревателя:
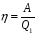
С другой стороны:

, где Т1- температура нагревателя, Т2- температура холодильника
Откуда

Подставляем числа:

Ответ:
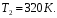
Задача №190
Плоский
конденсатор заполнен диэлектриком, и
на его пластины подана некоторая разность
потенциалов. Энергия конденсатора равна
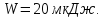 После того, как конденсатор отключили
от источника напряжения, диэлектрик
вынули из конденсатора, совершив работу
После того, как конденсатор отключили
от источника напряжения, диэлектрик
вынули из конденсатора, совершив работу
 Найти диэлектрическую проницаемость
Найти диэлектрическую проницаемость
 диэлектрика.
диэлектрика.
Дано:
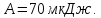
Найти:
Решение:
 =
=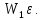 Работа, совершенная против сил кулоновского
притяжения, равна
Работа, совершенная против сил кулоновского
притяжения, равна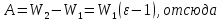

Ответ:
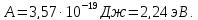
Задача №200.
Пространство между пластинами плоского конденсатора заполнено диэлектриком, диэлектрическая восприимчивость которого æ=0,08. Расстояние между пластинами d=5мм. На пластины конденсатора подана разность потенциалов U=4кВ. Найти поверхностную плотность связанных зарядов на диэлектрике и поверхностную плотность заряда на пластинах конденсатора.
Дано: æ=0,08; d=5мм, U=4кВ.
Найти:
 .
.
Решение.
Найдем напряженность между пластинами конденсатора:

Диэлектрическая проницаемость связана с диэлектрической восприимчивостью следующим выражением:
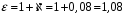
Запишем формулу для нахождения плотности связанных зарядов на пластинах конденсатора и, подставив значения в системе СИ, найдем искомую величину:
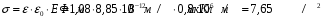
Запишем выражение для нахождения плотности связанных зарядов на диэлектрике и решим ее:

Ответ:

