
К.Р.№1, в-5(по зачетке)
.docЗадача 1

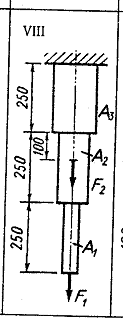
Исходные данные:
![]() ,
,
![]()
![]() ;
;![]()
![]()
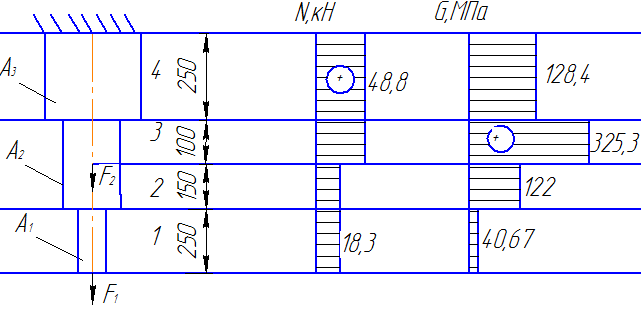
Решение:
1. Рассчитываем продольную силу на каждом участке:
![]()
![]()
2. Определяем нормальные напряжения на каждом участке:
![]()
![]()
![]()
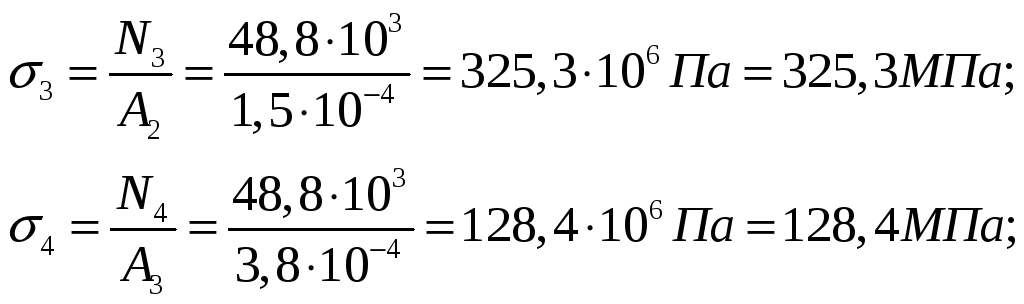
3. Определяем удлинение на каждом участке:
![]()
![]()
![]()
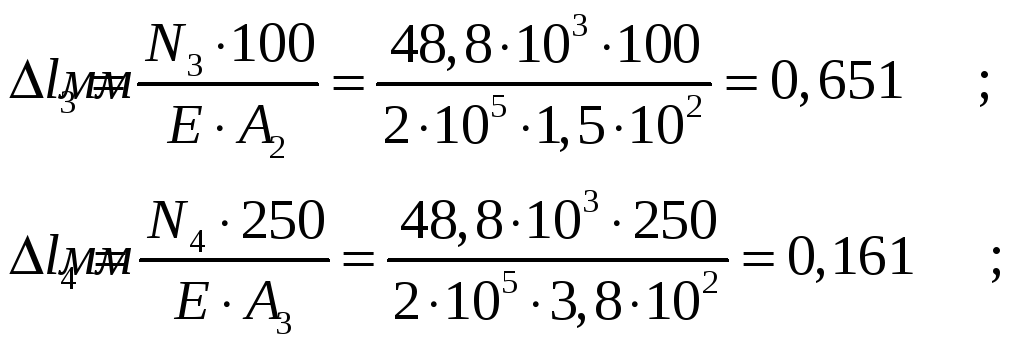
4. Определяем полное удлинение стержня:
![]()
Под действием заданных сил, брус удлиниться на 0,934 мм.
Задача 2

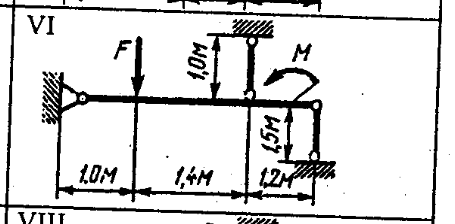
Исходные данные:
![]() ,
,
![]() ;
;![]()
Решение:
-
Мысленно избавляемся от заделки в стержнях, заменяя ее на реакции.
-
Составляем уравнения равновесия и определяем неизвестные:


Для проверки составляем еще одно уравнение равновесия:
![]()

3. Вычисляем площади поперечных сечений стержней из условия прочности:
![]()
- площадь поперечного сечения стержня 1:
![]()
- площадь поперечного сечения стержня 2:
![]()
-
Определяем размер поперечного сечения каждого стержня:
![]()
- размер поперечного сечения стержня 1:
![]()
Принимаем
![]()
- размер поперечного сечения стержня 2:
![]()
Принимаем
![]()
5. Напряжения в поперечных сечениях стержня 1:

Стержень 1
перегружен на
![]()
Напряжения в поперечных сечениях стержня 2:
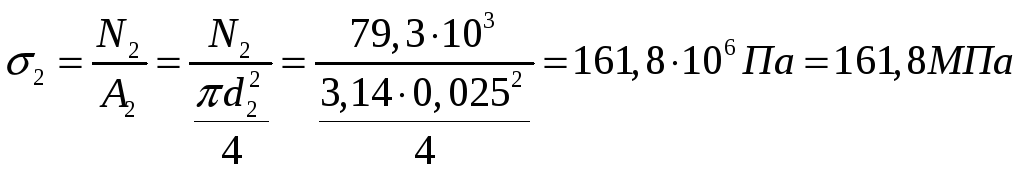
Стержень 2
перегружен на
![]()
Вывод: напряжение стержня 1 выше допускаемого всего на 3,75%, а стержня 2 – на 1,125%, следовательно, прочность стержней обеспеченна, так как превышение может составлять до 5% от допускаемого напряжения.
Задача 3

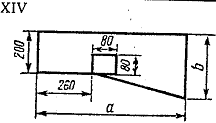
Исходные данные:
![]() ,
,
![]() ;
;
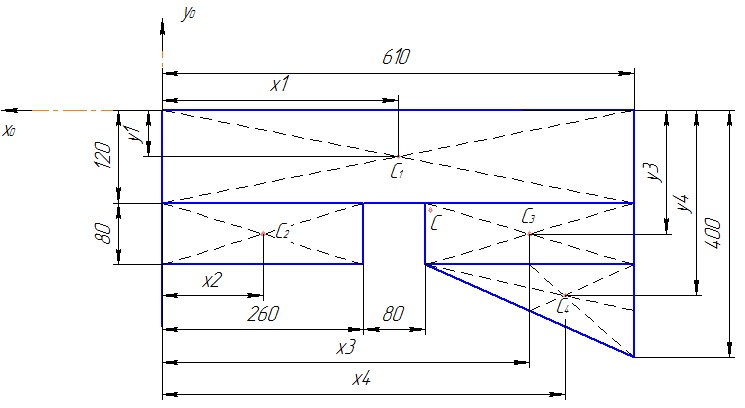
1. Разбиваем сечение на элементы простой формы:
1 –прямоугольник
![]() с центром тяжести
с центром тяжести
![]() ;
;
2 –прямоугольник
![]() с центром тяжести
с центром тяжести
![]() ;
;
3 – прямоугольник
![]() с центром тяжести
с центром тяжести
![]() ;
;
4 - треугольник
![]() с центром тяжести
с центром тяжести
![]() ;
;
2. Проводим
вспомогательные оси координат![]() .
.
3. Находим координаты центров тяжести каждой фигуры:
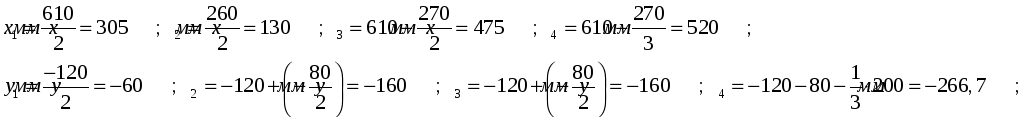
4. Определяем площади каждой фигуры:
![]()
![]()
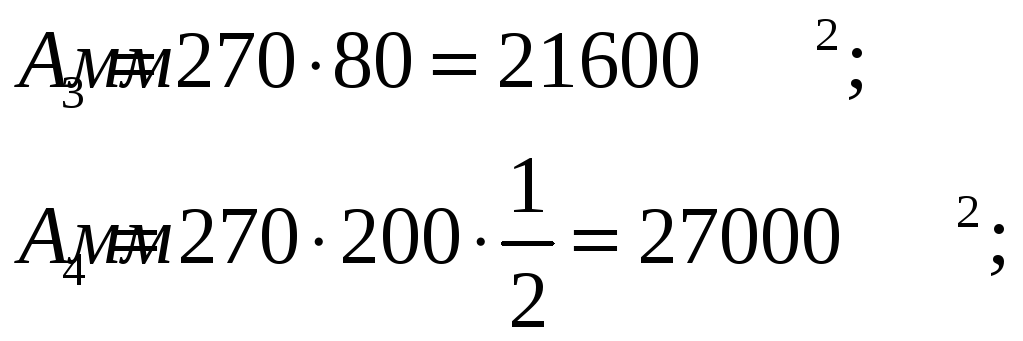
5. Определяем координату центра тяжести:
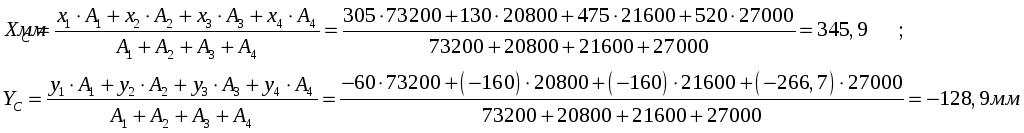
Ответ:
![]()
Задача 4

Исходные данные:
![]()
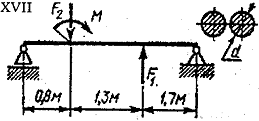
Решение:
1. Для определения реакций опор составим два уравнения равновесия балки:

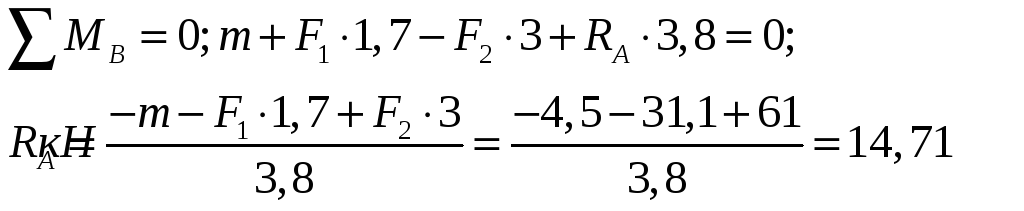
Для проверки составляем еще одно уравнение равновесия:
![]()
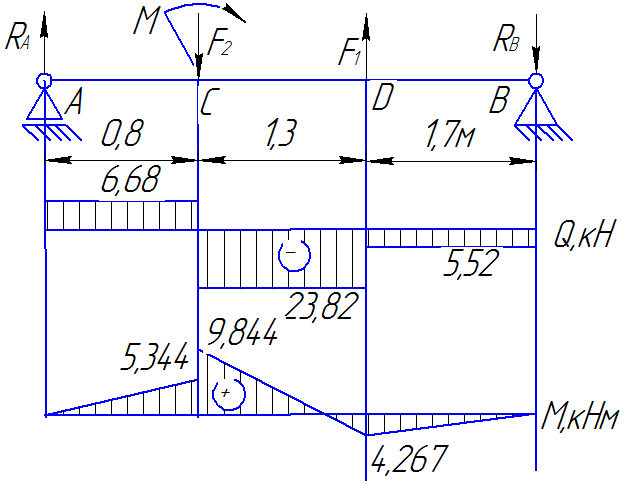
2. Делим балку на три участка.
3. Определяем поперечные силы в сечениях:
![]()
![]()
![]()
4. Вычисляем изгибающие моменты:
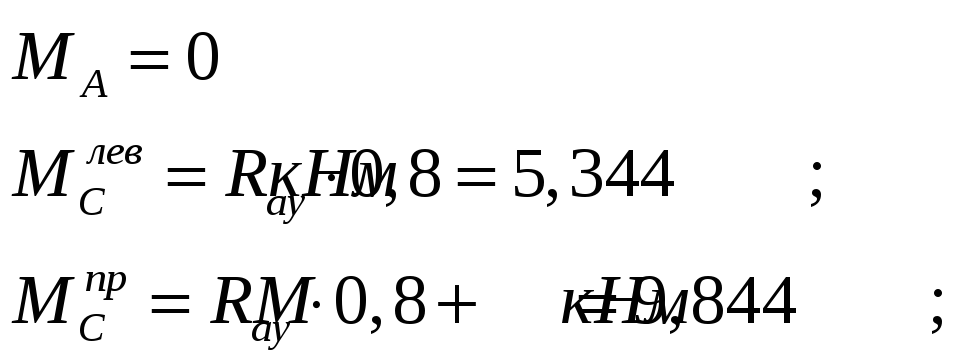
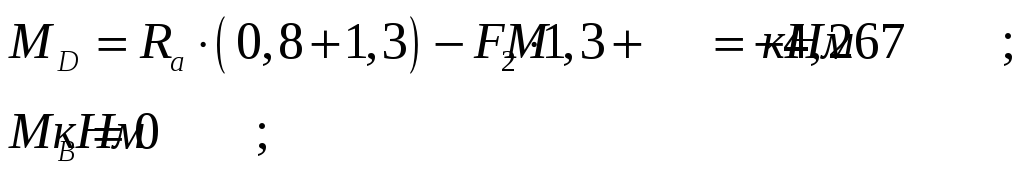
-
Определяем момент сопротивления поперечного сечения балки относительно нейтральной оси:
![]()
Балка состоит
из двух сечений. Определим момент
сопротивления для одного сечения:
![]()
6. Подбираем круглое
сечение с соотношением сторон
![]()
Момент сопротивления:
![]() .
.
Принимаем
![]()
Задача 5

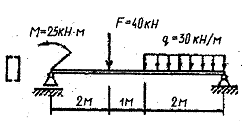
Решение:
1. Для определения реакций опор составим два уравнения равновесия балки:
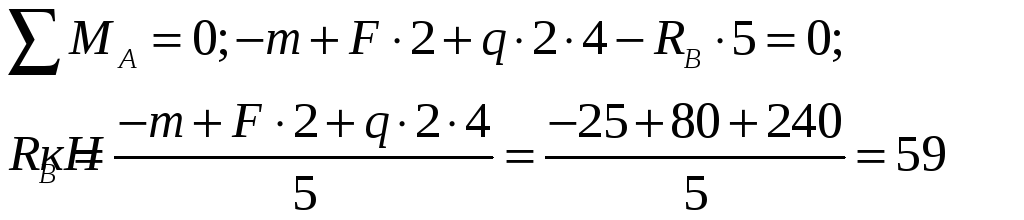
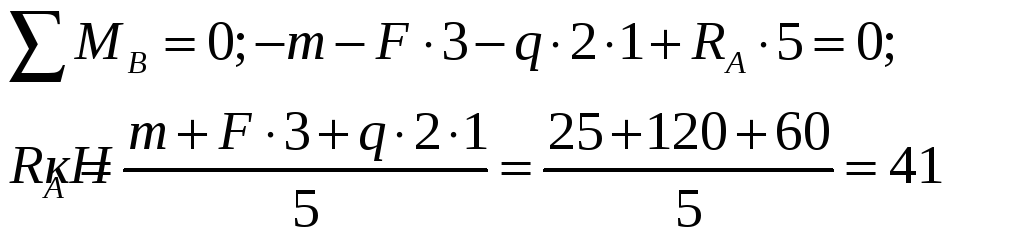
Для проверки составляем еще одно уравнение равновесия:
![]()
2. Делим балку на три участка.
3. Определяем поперечные силы в сечениях:
![]()
![]()
![]()
4. Вычисляем изгибающие моменты:
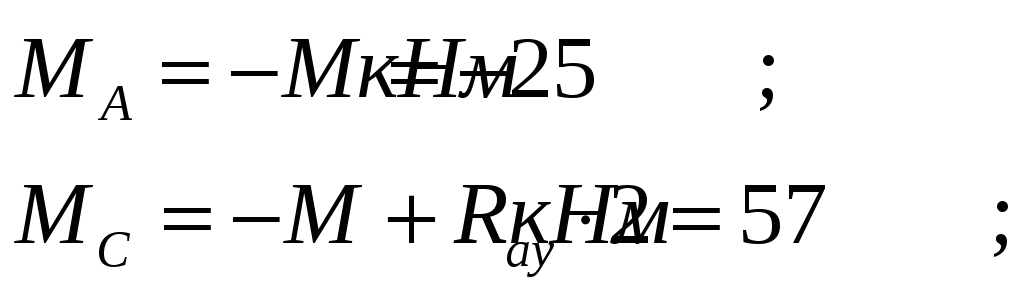
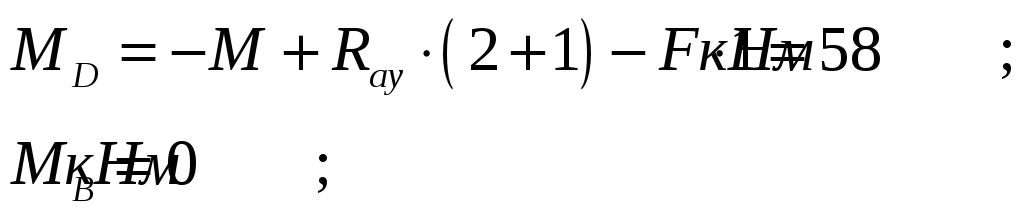
-
Определяем момент сопротивления поперечного сечения балки из условий прочности:
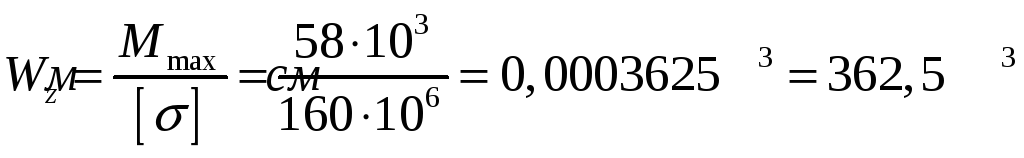
Балка состоит
из двух швеллеров. Определим момент
сопротивления для одного сечения:
![]()
Выбираем по ГОСТ
8239-89 два швеллера №20, у которых
![]() .
.
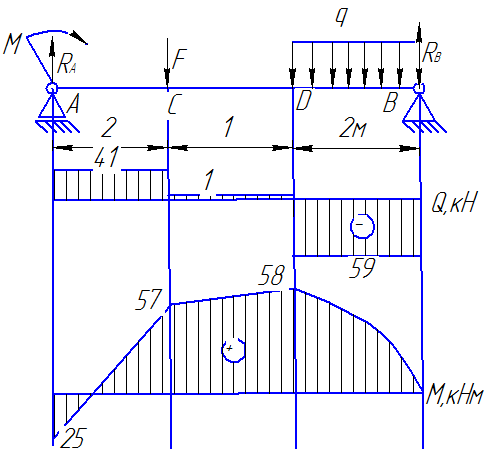
Задача 6


Исходные данные:
![]() ;
;![]()

Решение:
1. Изображаем вал со всеми действующими на него силами, а также оси координат.
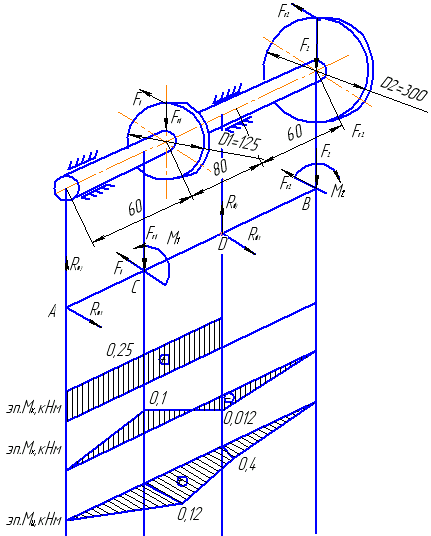
2. Определяем вращающий момент, действующий на вал:
![]()
3. вычисляем нагрузки, приложенные к валу:
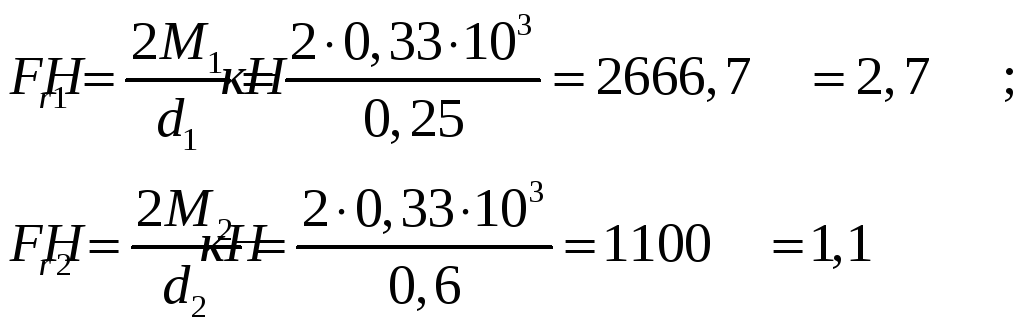 ;
;
![]()
3. Составляем шесть уравнений равновесия:

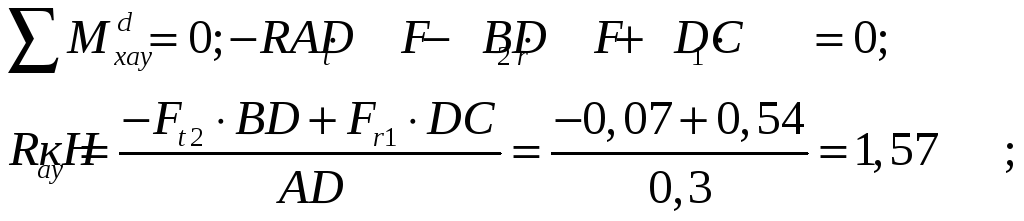
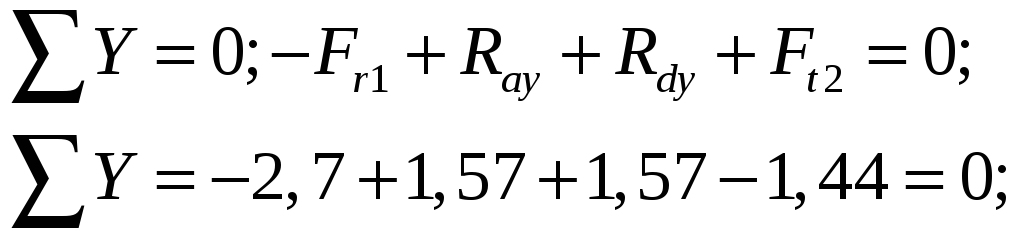
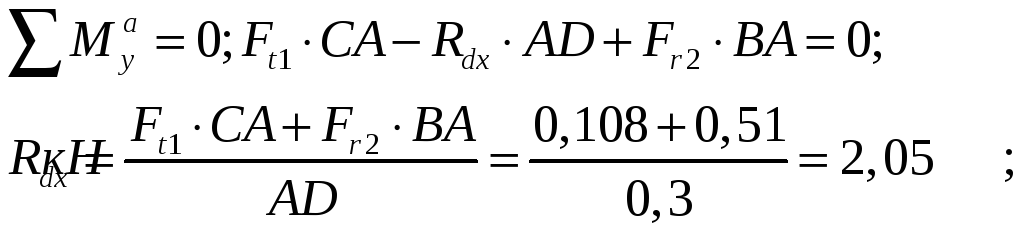

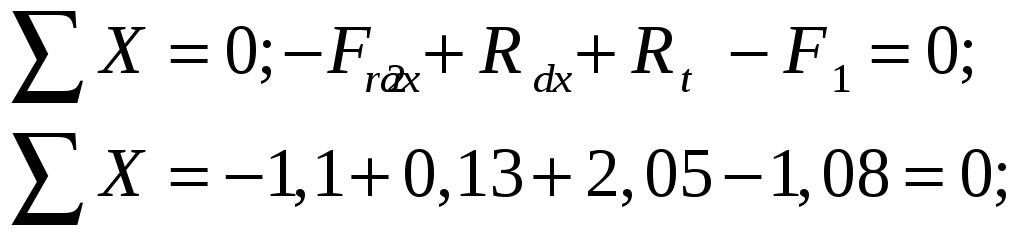
4. Строим эпюру
крутящих моментов
![]() .
.
5. Строим эпюру изгибающих моментов в вертикальной и горизонтальной плоскостях:

6. Наибольшее значение эквивалентного момента:
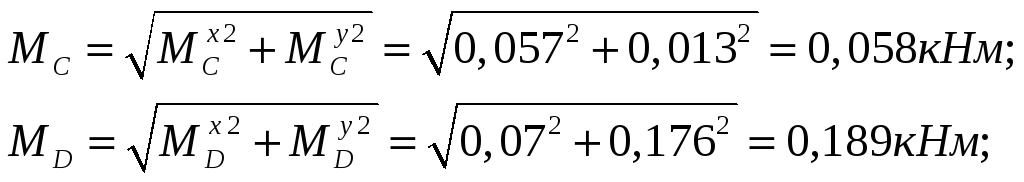
Опасным является сечение D.
![]()
7. Требуемый размер вала:
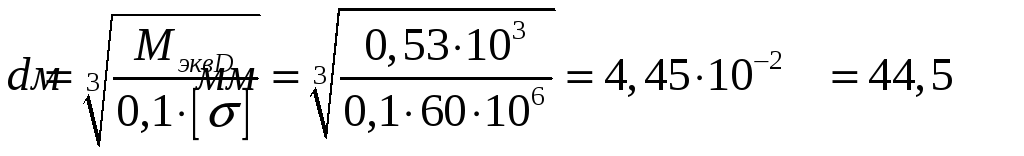
Принимаем d = 45мм.
Задача 7

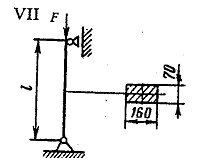
Исходные данные:
![]()
![]()
![]() ,
,
![]()
Решение:
1. Определяем момент инерции сечения:
![]()
2. Определяем площадь поперечного сечения стойки:
![]() ,
,
3. Опеределяем радиус инерции:
![]()
4. При данном способе
закрепления концов коэффициент приведения
длины
![]() .
.
5. Определяем гибкость стойки:
![]()
6. Находим критическую силу:
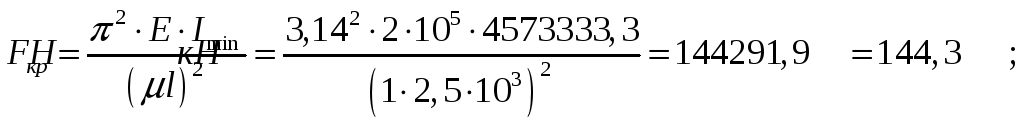
7. Определяем коэффициент запаса устойчивости:
![]()
Балка заданную нагрузку выдержит.
Список используемой литературы:
-
«Основы Технической механики» М.С.Мовнин, А.Г.Рубашкин издательство «Судостроение» Ленинград 1973г.
-
Руководство к решению задач по технической механике.
-
Таблицы сортамента стандартных профилей.
-
Методическое указание «Техническая механика» для учащихся-заочников средних специальных учебных заведений строительных специальностей. – 2-е изд./Т.Н. Мазурина. – М.: Высш.шк., 1986.
-
Сборник задач по технической механике. Учеб. Пособие для строительных специальностей техникумов. М., «Высш.школа», 1978.
-
«Техническая механика» Учеб. Для машиностр. спец.техникумов/А.А.Эрдеди, Ю.А. Медведев, Н.А.Эрдеди. – 3-е изд., перераб. и доп. – М., Высш.шк., 1991.
