Лекция№10 Дифференциальное исчисление функций одной действительной переменной

3.1.Задачи, приводящие к понятию производной.

Рассмотрим движение материальной точки по оси . Координата материальной точки является дифференцируемой функцией времени . В момент времени материальная точка имеет координату . В момент времени материальная точка приобрела координату . Посчитаем среднюю скорость перемещения материальной точки за промежуток времени

.

Если устремить к нулю и рассмотреть , равный мгновенной скорости материальной точки , то можно заметить, что = = , т.е. предел отношения приращения координаты материальной точки к приращению времени и есть с одной стороны производная координаты по времени, а с другой стороны - мгновенная скорость материальной точки.

Сила тока: Пусть - это количество электричества, проходящего через фиксированное сечение провода за время .

Средняя сила тока

-сила тока в момент

3. 2. Определение производной

Пусть и - значения аргумента, а и - соответствующие значения функции . Разность называется приращением аргумента, а разность - приращением функции на отрезке .

Производной от функции по аргументу называется конечный предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю:

; или

(производная обозначается также ).

Отыскание производной называется дифференцированием функции.

3.3. Геометрический и механический смысл производной.

Легко выяснить геометрический смысл производной и дифференциала функции. Введем сначала общее определение касательной к кривой. Возьмем на непрерывной кривой две точки и (рис. 12).

Прямую , проходящую через эти точки, называют секущей. Пусть точка двигаясь вдоль кривой , неограниченно приближается к точке . Тогда секущая, поворачиваясь около точки , стремиться к некоторому предельному положению .

Касательной к данной кривой в данной точке М называется предельное положение секущей , проходящей через точку М, когда вторая точка пересечения неограниченно приближается по кривой к точке . Касательная к графику функции образует угол с осью Ох. Секущая образует с осью угол . Угловой коэффициент секущей = = . При приближении точки к точке секущая, поворачиваясь около точки , переходит в касательную. Угол наклона касательной стремится к углу наклона касательной , т.е. . Поэтому угловой коэффициент касательной равен производной от ординаты по абсциссе

= = = = .

3.4. Уравнение касательной и нормали к графику функции

Рассмотрим график функции . Выберем точку , принадлежащую кривой, и проведем через эту точку касательную. Касательная как наклонная прямая линия, проходящая через точку , имеет уравнение вида

.

Угловой коэффициент касательной равен производной функции, посчитанной в точке касания , т.е. . В результате получаем уравнение касательной к графику функции в точке (рис. 13)

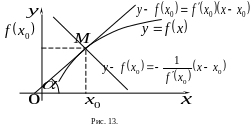
Нормалью к кривой в точке , принадлежащей графику, называется прямая линия, проходящая через эту точку перпендикулярно касательной. Поскольку угловые коэффициенты перпендикулярно расположенных прямых связаны соотношением

, то уравнение нормали, проходящей через точку , имеет вид

.

Пример. Написать уравнение касательной и нормали к графику функции в точке .

Решение. Так как производная в точке равна , а значение функции , то уравнение касательной имеет вид

или .

Уравнение нормали имеет вид

или .