Лекция№14

Исследование функций и построение графика функции

3.26. Локальные экстремумы функции

Точка называется точкой максимума (точкой минимума) функции , если существует такая -окрестность точки, что для всех остальных значений из этой окрестности будет выполняться неравенство

, .

Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом функции.

Понятие экстремума функции является локальным для функции, поскольку всегда связано с определенной окрестностью точки из области определения функции. Необходимо отметить, что точки экстремумов могут быть только внутренними точками области определения. Рассмотрим необходимое условие существования экстремума функции.

Теорема 1. (Необходимое условие экстремума). Если дифференцируемая функция имеет в точке максимум или минимум, то ее производная обращается в нуль в этой точке, т.е

.

Доказательство. Рассмотрим случай, когда точка является точкой максимума. Это означает, что в окрестности точки выполняется неравенство  или . Но тогда

если , и если . Так как производная

по условию теоремы существует, а

, ,

то получаем, что .

Геометрический смысл теоремы состоит в том, что в точке экстремума дифференцируемой функции касательная к её графику параллельна оси .

Точки, в которых производная обращается в нуль называются стационарными.

Однако, можно привести ряд примеров, когда обращение в нуль производной не связано с наличием экстремума. Например, для функции её производная равна нулю при , но в начале координат функция не имеет экстремума.

Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция в точке производной не имеет, но точка является точкой минимума. Можно утверждать, что непрерывная функция имеет экстремум или в точках, где производная функции равна нулю, или не существует. Подобные точки называются критическими точками первого рода.

Теорема 2. (Достаточное условие экстремума). Если непрерывная функция дифференцируема в некоторой -окрестности критической точки и при переходе через нее слева направо производная меняет знак с плюса на минус, то есть точка максимума; если же изменение знака происходит с минуса на плюс, то является точкой минимума.

Доказательство. Предположим, что производная при переходе через точку слева направо меняет знак с плюса на минус. Тогда функция возрастает на промежутке и убывает на промежутке . Отсюда следует, что значение в точке является наибольшим на ин­тервале , что соответствует определению максимума функции в точке .

Аналогичным образом можно рассмотреть случай изменения знака производной с минуса на плюс при переходе через точку .

Пример 1.. Найти экстремум функции у =

Решение: Областью определения функции является вся числовая ось. Находим производную .

Производная непрерывной функции не существует при и равна нулю при . Две критические точки разбивают всю область определения функции на три интервала , , . Определим знаки производной на каждом из трех интервалов.

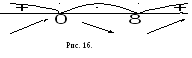
Следовательно, является точкой максимума, причем, , а является точкой минимума, .

В некоторых задачах удобнее использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.

Теорема 3. (Второй достаточный признак существования экстремума). Если в точке первая производная функции равна нулю, а вторая производная в точке существует и отлична от нуля , то при <0 в точке функция имеет максимум, а при > функция имеет минимум.

Доказательство. Пусть для определенности >. Так как

то в окрестности точки . Если <0, то<0; если >0, то >0. При переходе через точку первая производная меняет знак с минуса на плюс. По предыдущей теореме есть точка минимума.

Аналогично доказывается, что если < 0, то в точке функция имеет максимум.