
 ____________________________________________
____________________________________________
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Брянский государственный технический университет
____________________________________________________________
“УТВЕРЖДАЮ”
Ректор университета
__________А.В. Лагерев
“____”___________2006 г.
МАТЕМАТИКА
АЛГЕБРА И ГЕОМЕТРИЯ
Методические указания и контрольные задания
для студентов специальности “Программное обеспечение
вычислительной техники и автоматизированных
систем” заочной формы обучения (1 семестр)
Второе издание, исправленное и переработанное
Брянск 2006
УДК 516.1/4
Математика. Алгебра и геометрия. Методические указания и контрольные задания для студентов специальности “Программное обеспечение вычислительной техники и автоматизированных систем” заочной формы обучения (1 семестр). − 2-е изд., испр. и перераб. –Брянск: БГТУ, 2006 − 18 с.
Алексей Петрович Мысютин
канд. техн. наук, доцент
Рекомендовано кафедрой “Высшая математика” БГТУ
(протокол №1 от 31.08.2006 г.)
Печатается по изданию: Математика. Алгебра и геометрия. Методические указания и контрольные задания для студентов специальности “Программное обеспечение вычислительной техники и автоматизированных систем” заочной формы обучения (1 семестр). − Брянск: БГТУ, 2004.
Студенты первого курса заочной формы обучения специальности “Программное обеспечение вычислительной техники и автоматизированных систем” в первом семестре должны выполнить две контрольные работы. В первой работе представлены задания по разделу «Линейная алгебра», а во второй − по разделу «Векторная алгебра».
Необходимые теоретические сведения из указанных разделов высшей математики и примеры решения типовых задач изложены в следующих учебных пособиях:
Беклемишев, Д.В. Курс аналитической геометрии и линейной алгебры /Д.В. Беклемишев. – М.: Физматлит, 2001. – 376 с.
Бугров, Я.С., Никольский, С.М. Высшая математика / Я.С. Бугров, С.М. Никольский. Т.1. Элементы линейной алгебры и аналитической геометрии. – М.: Дрофа, 2003.– 288 с.
Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − 2-е изд., испр. − М.: Айрис-пресс, 2002. – Ч. 1. − 288 с.
Данко, П.Е., Попов, А.Г., Кожевникова, Т.Я. Высшая математика в упражнениях и задачах / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. шк., 1999. – Ч. 1. – 304 с.
Ефимов Н.В. Краткий курс аналитической геометрии / Н.В. Ефимов. – М.: Физматлит, 2002. – 240 с.
Считая базовым учебник [3], укажем темы, которые необходимо изучить студенту для успешного выполнения контрольных работ.
Контрольная работа №1.
Тема 1. Матрицы
Основные понятия. Литература: [3], §1, п. 1.1.
Действия над матрицами. Литература: [3], §1, п. 1.2.
Тема 2. Определители
Основные понятия. Литература: [3], §2, п. 2.1.
Свойства определителей. Литература: [3], §2, п. 2.2.
Тема 3. Невырожденные матрицы
Основные понятия. Литература: [3], §3, п. 3.1.
Обратная матрица. Литература: [3], §3, п. 3.2.
Ранг матрицы. Литература: [3], §3, п. 3.3.
Тема 4. Системы линейных алгебраических уравнений
Основные понятия. Литература: [3], §, п. 4.1.
Решение систем линейных уравнений. Литература: [3], §4, п. 4.2.
Матричный метод решения систем линейных уравнений. Формулы Крамера. Литература: [3], §4, п. 4.3.
Решение систем линейных уравнений методом Гаусса. Литература: [3], §4, п. 4.4.
Системы линейных однородных уравнений. Литература: [3], §4, п. 4.5.
Тема 5. Собственные векторы и собственные значения матриц
Литература: [4], гл. V, §4, п. 4.
Контрольная работа №2.
Тема 1. Векторы
Основные понятия. Литература: [3], §5, п. 5.1.
Линейные операции над векторами. Литература: [3], §5, п. 5.2.
Проекция вектора на ось. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы. Действия над векторами, заданными проекциями. Литература: [3], §5, п. 5.3–5.5.
Тема 2. Скалярное произведение векторов
Определение скалярного произведения. Литература: [3], §6, п. 6.1.
Свойства скалярного произведения. Выражение скалярного произведения через координаты. Литература: [3], §6, п. 6.2, 6.3.
Некоторые приложения скалярного произведения. Литература: [3], §6, п. 6.4.
Тема 3. Векторное произведение векторов
Определение векторного произведения. Литература: [3], §7, п.7.1.
Свойства векторного произведения. Выражение векторного произведения через координаты. Литература: [3], §7, п. 7.2, 7.3.
Некоторые приложения векторного произведения. Литература: [3], §7, п. 7.4.
Тема 4. Смешанное произведение векторов
Определение смешанного произведения. Литература: [3], §8, п.8.1.
Свойства смешанного произведения. Выражение смешанного произведения через координаты. Литература: [3], §8, п. 8.2, 8.3.
Некоторые приложения смешанного произведения. Литература: [3], §8, п. 8.4.
Первая контрольная работа состоит из шести заданий. Вторая работа состоит из восьми заданий. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой номера его зачетной книжки. Заметим, что каждое задание 6 контрольной работы №1 включает в себя две задачи: а) и б). В контрольной работе №2 задание 7а выполняется только в вариантах 1–5, в остальных вариантах выполняется задание 7б.
Задания контрольной работы №1
Даны матрицы
![]()
где n – номер варианта (n = 1,2,3,4,5,6,7,8,9,0). Найти значения , при которых определитель матрицы А’В+Е равен нулю (А’ – транспонированная матрица для матрицы А, Е – единичная матрица 4-го порядка).
Решить систему линейных алгебраических уравнений по формулам Крамера, с помощью обратной матрицы и методом Гаусса.
Вариант
1.
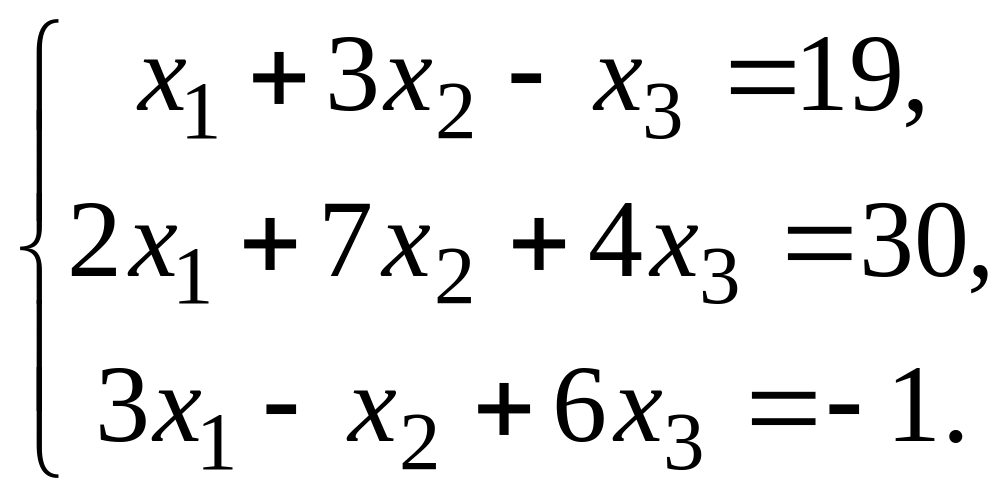
Вариант
2.
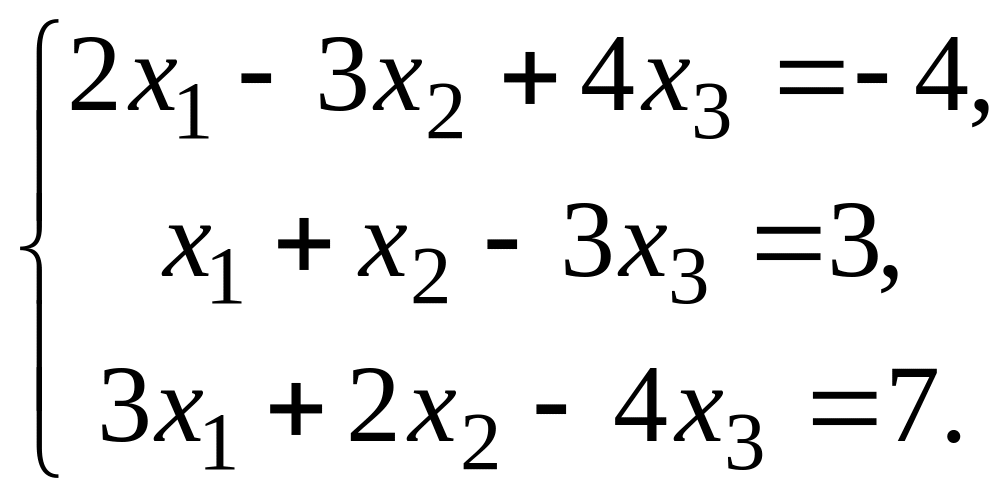
Вариант
3.
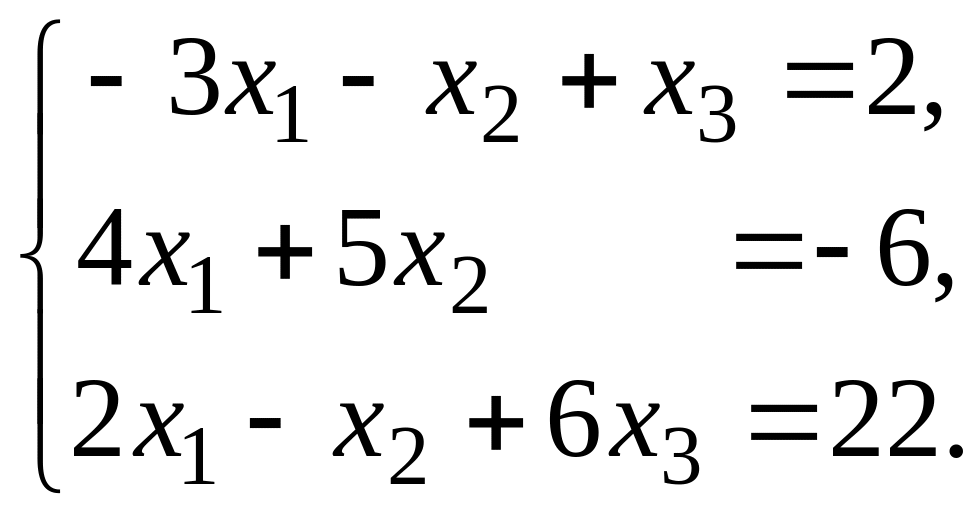
Вариант
4.
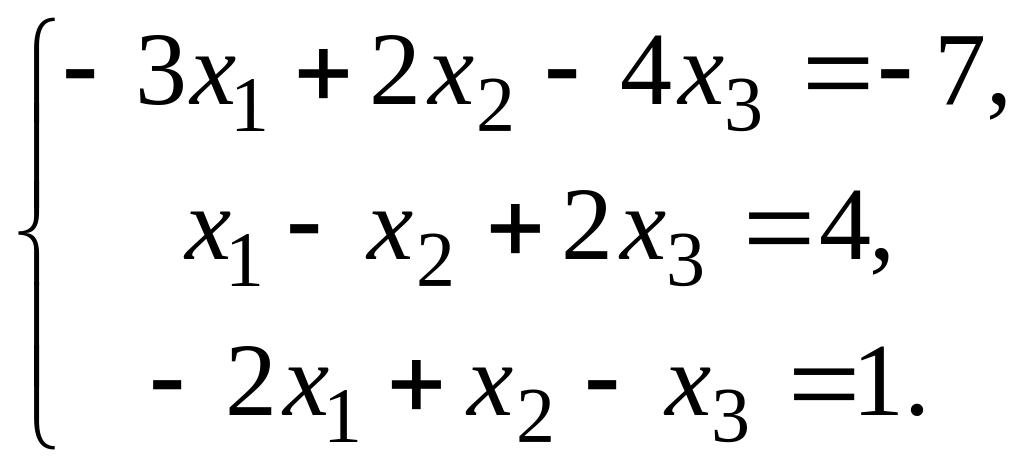
Вариант
5.
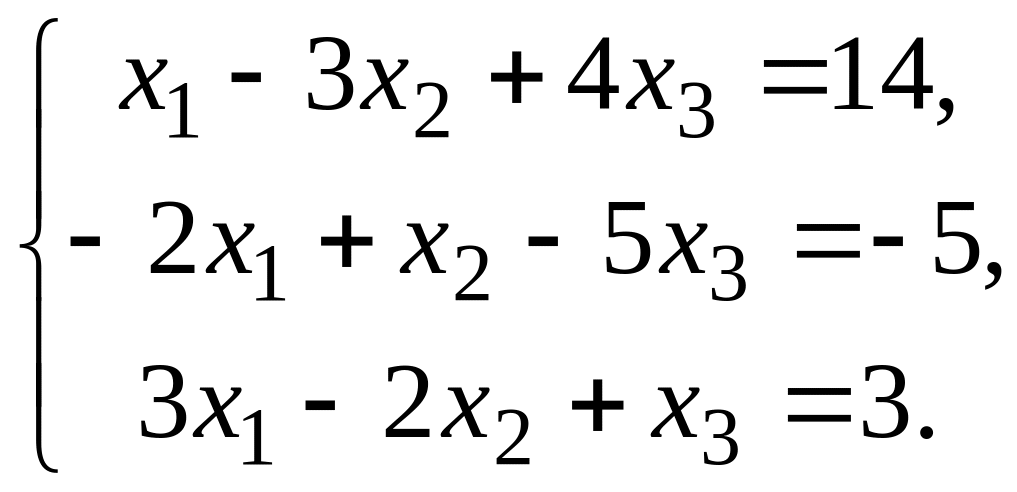
Вариант
6.

Вариант
7.
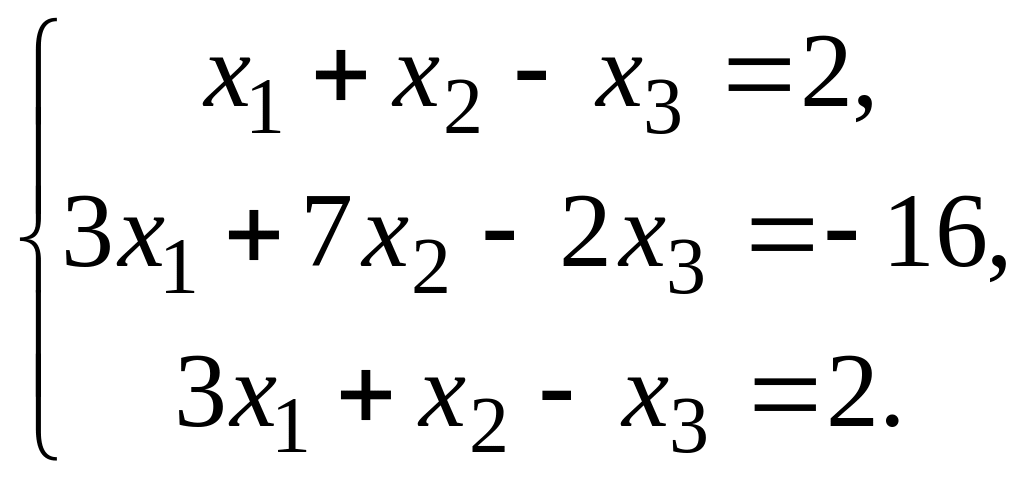
Вариант
8.
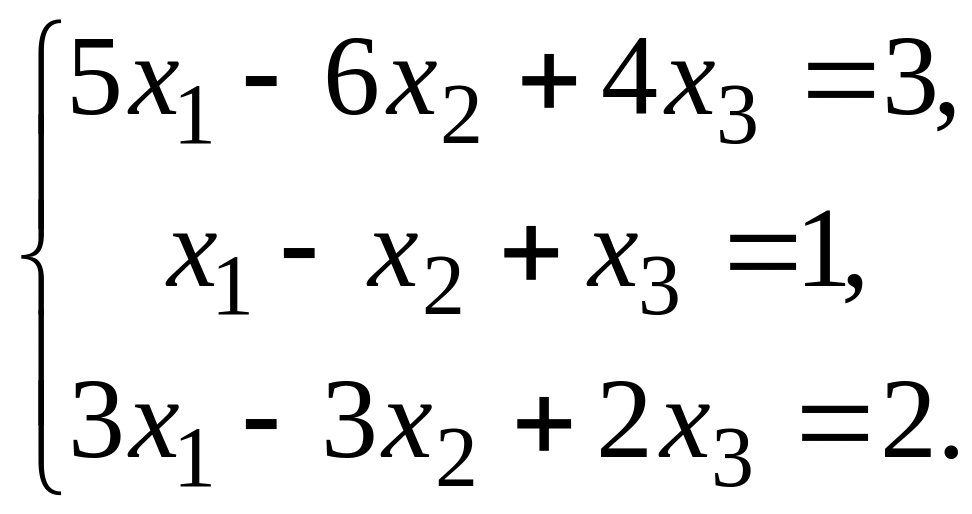
Вариант
9.
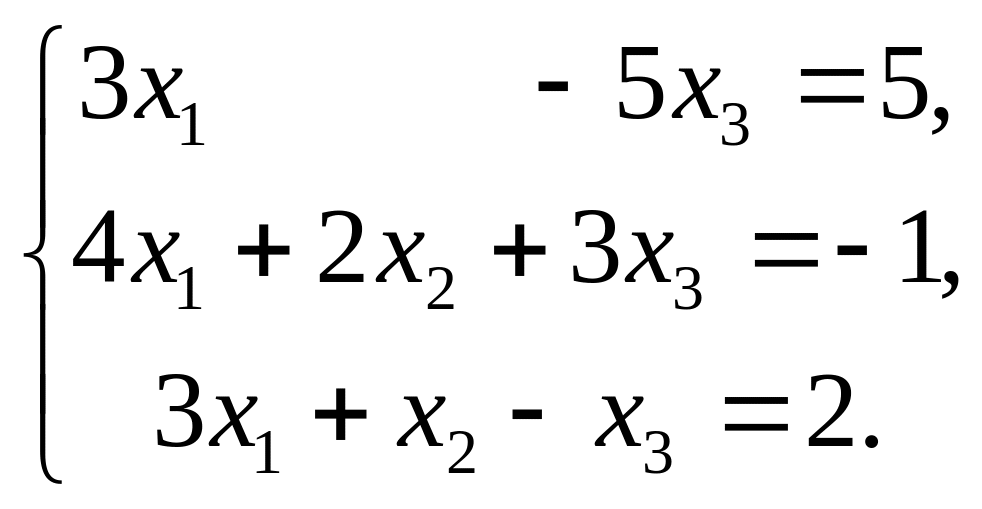
Вариант
0.
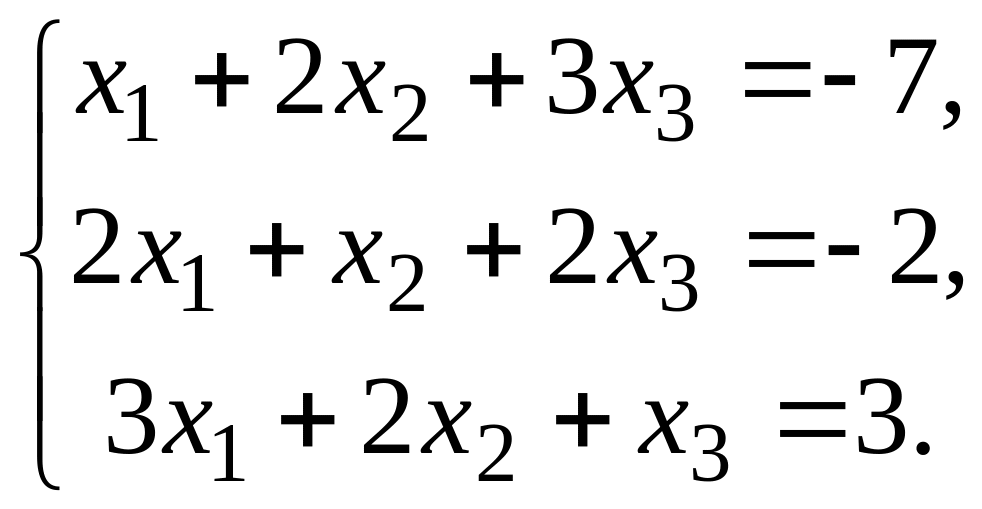
Найти матрицу Х из уравнения.
Вариант 1
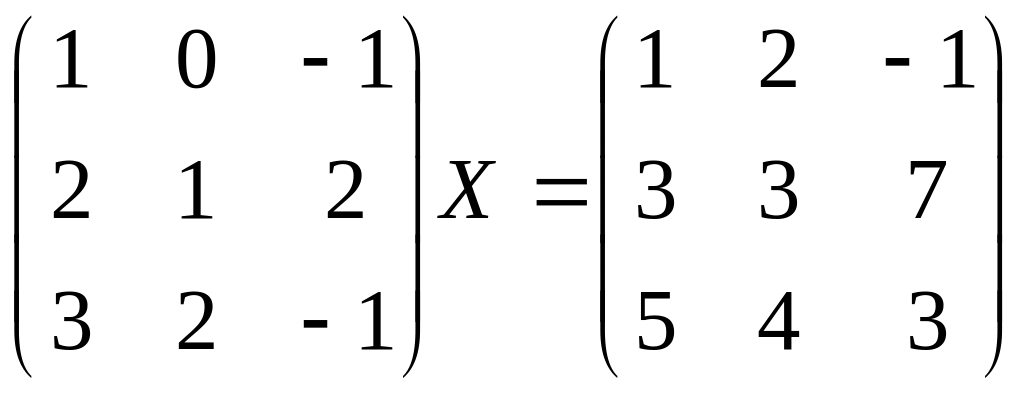
Вариант 2
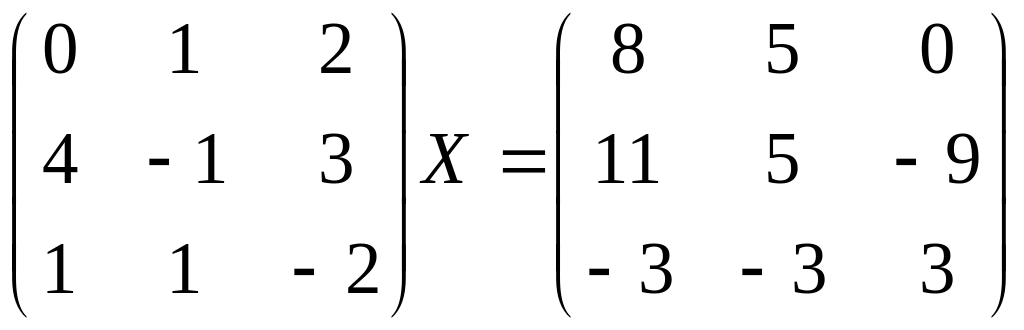
Вариант 3
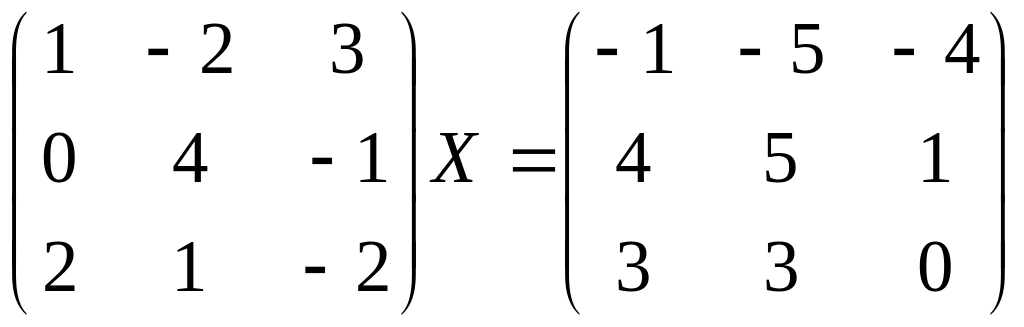
Вариант 4
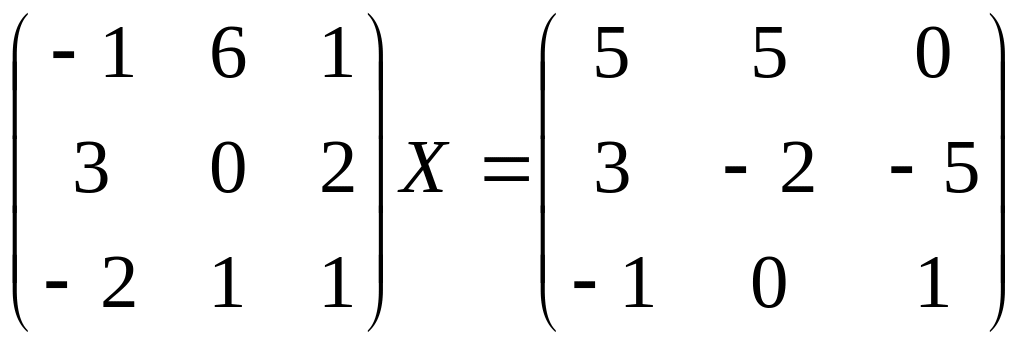
Вариант 5
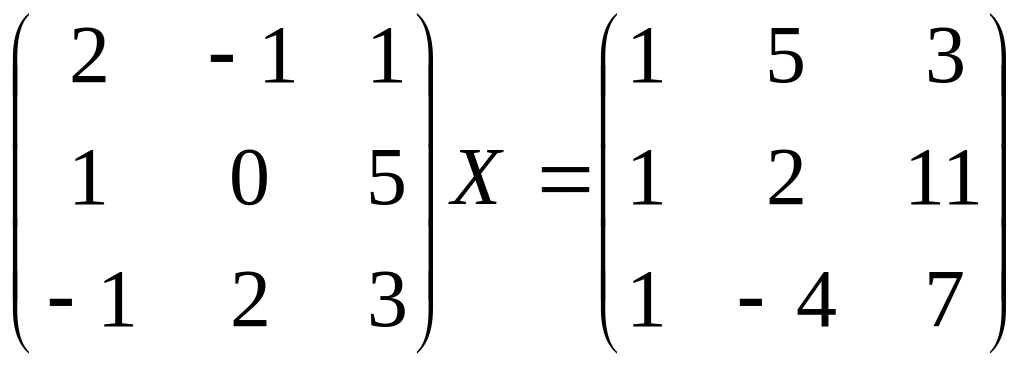
Вариант 6
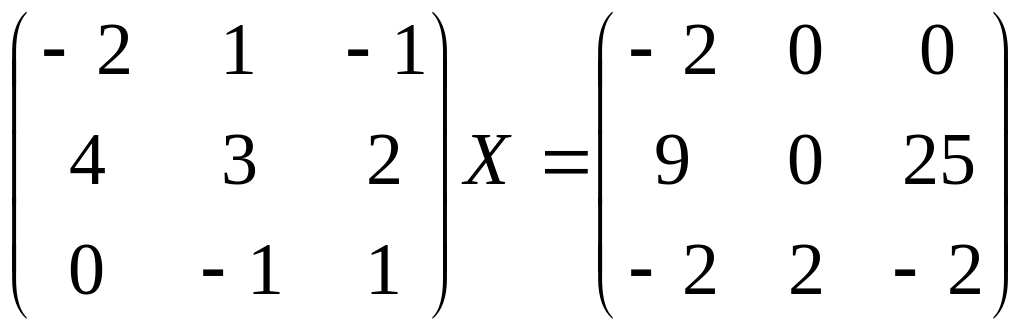
Вариант 7
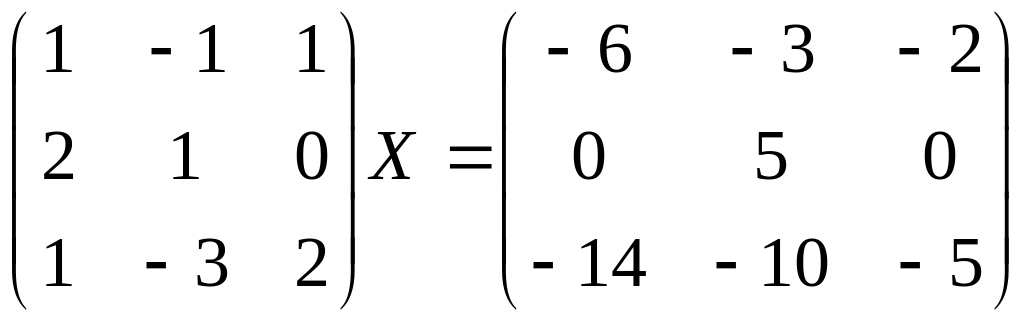
Вариант 8
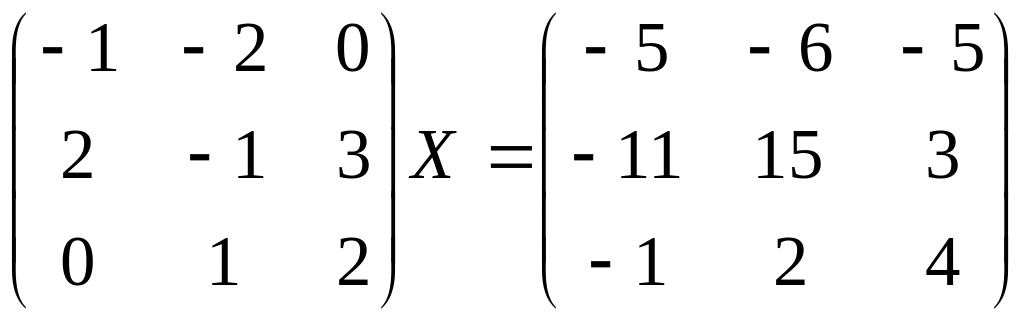
Вариант 9
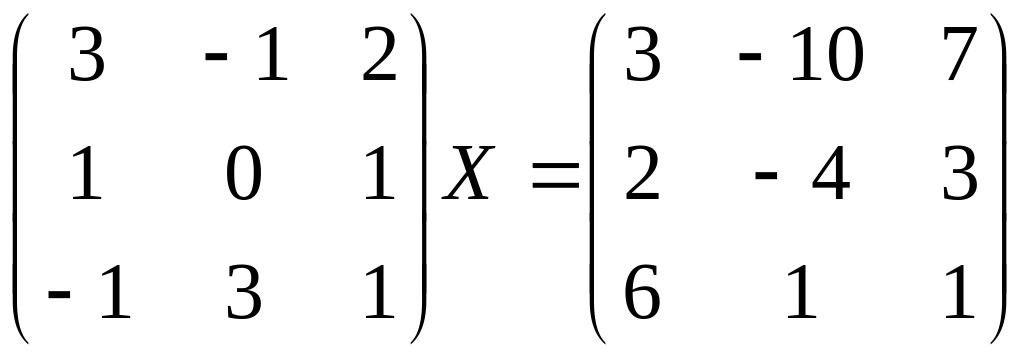
Вариант 0
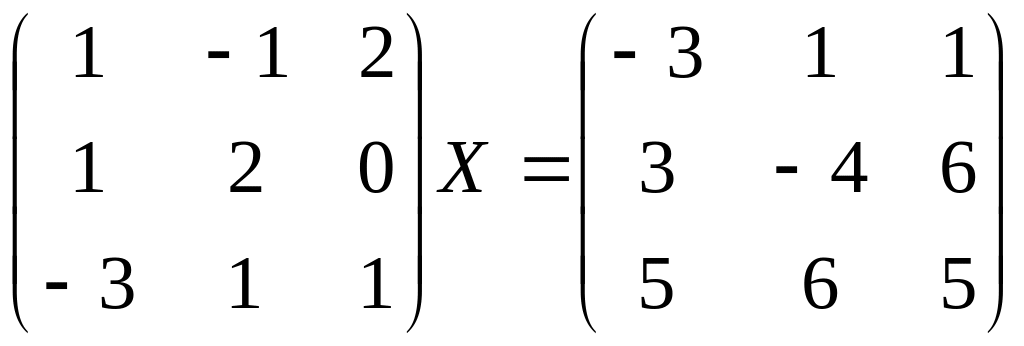
Найти ранг матрицы.
Вариант 1 Вариант 2
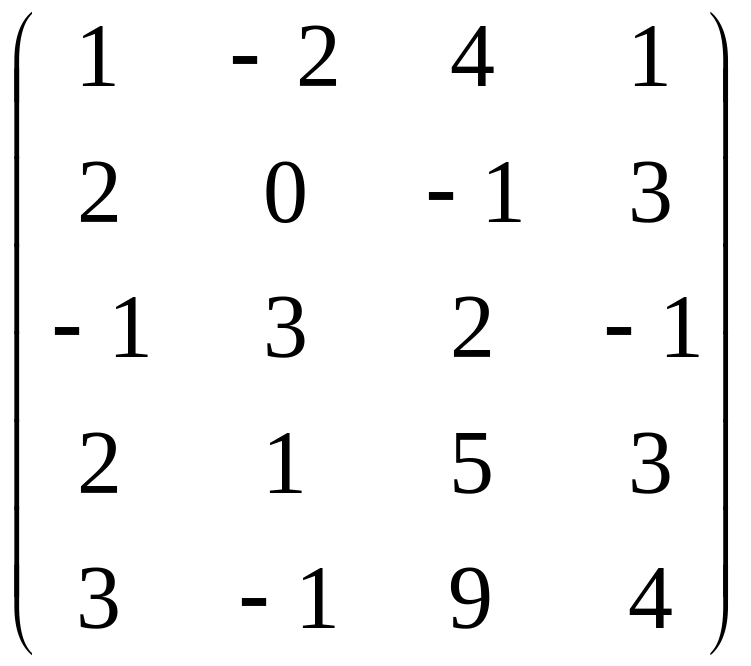
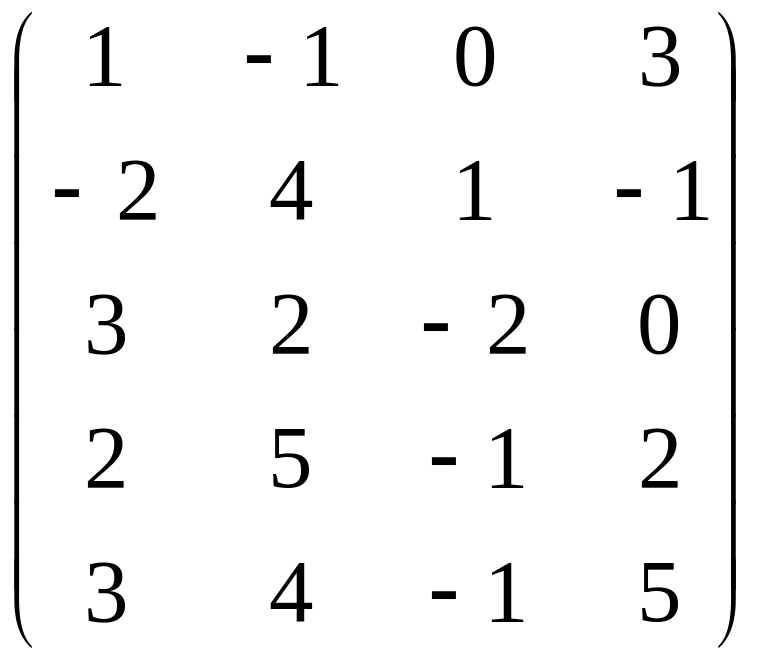
Вариант 3 Вариант 4
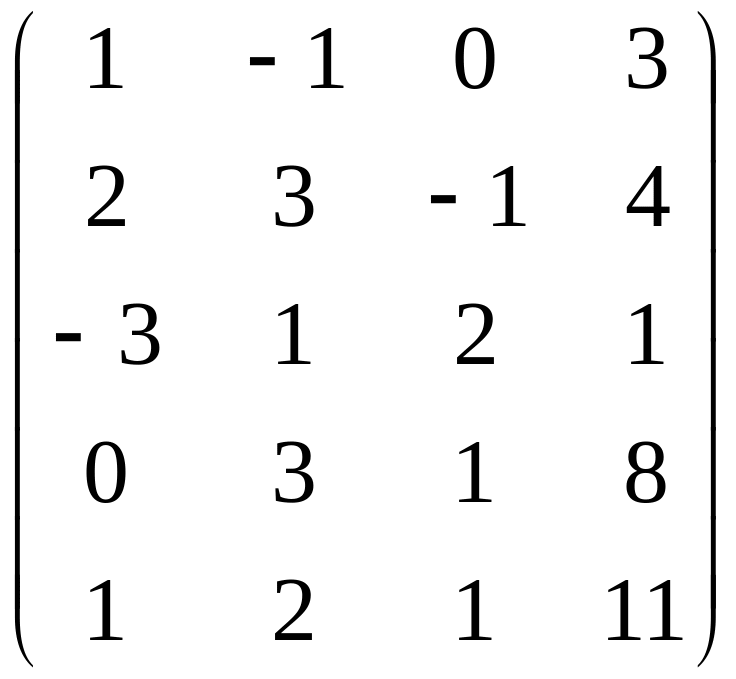
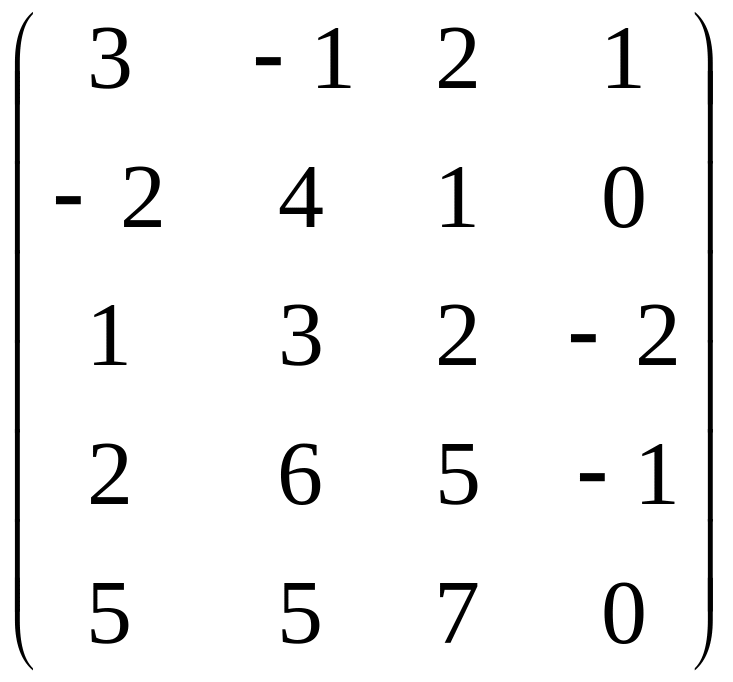
Вариант 5 Вариант 6
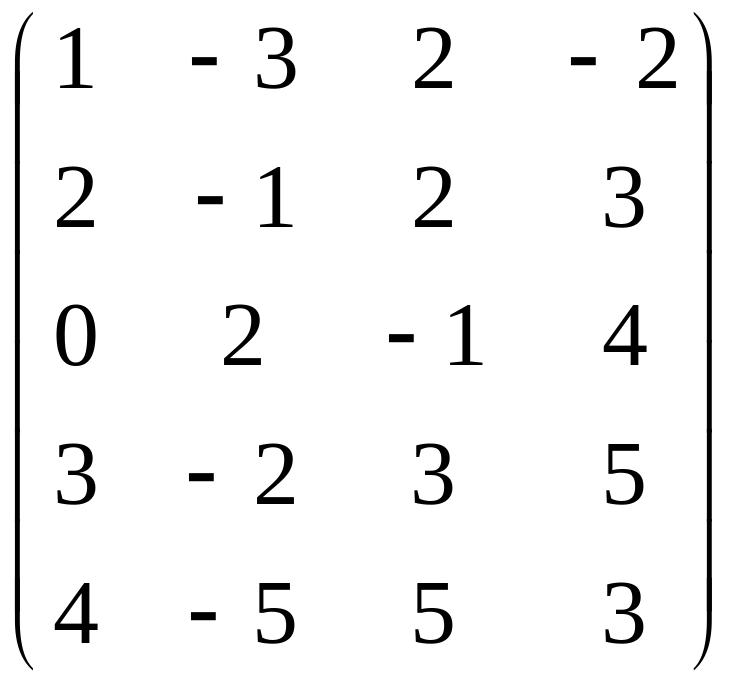
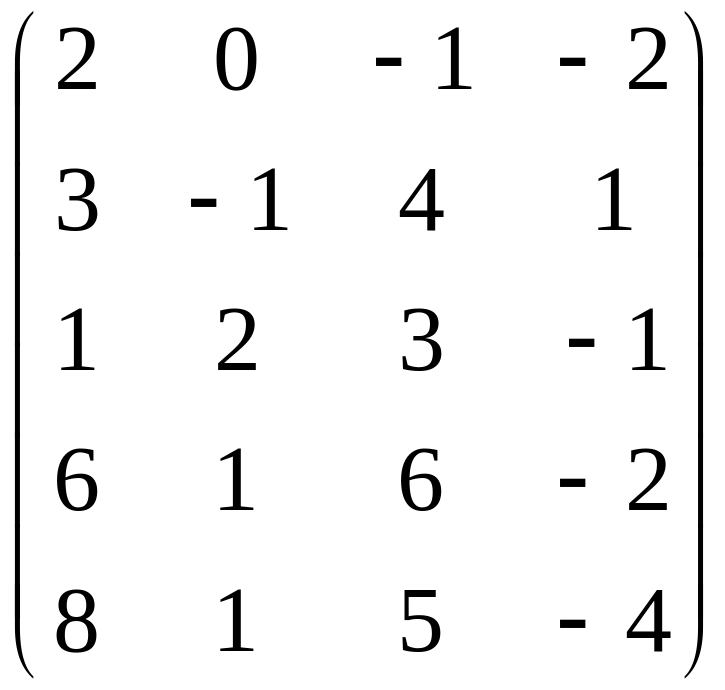
Вариант 7 Вариант 8
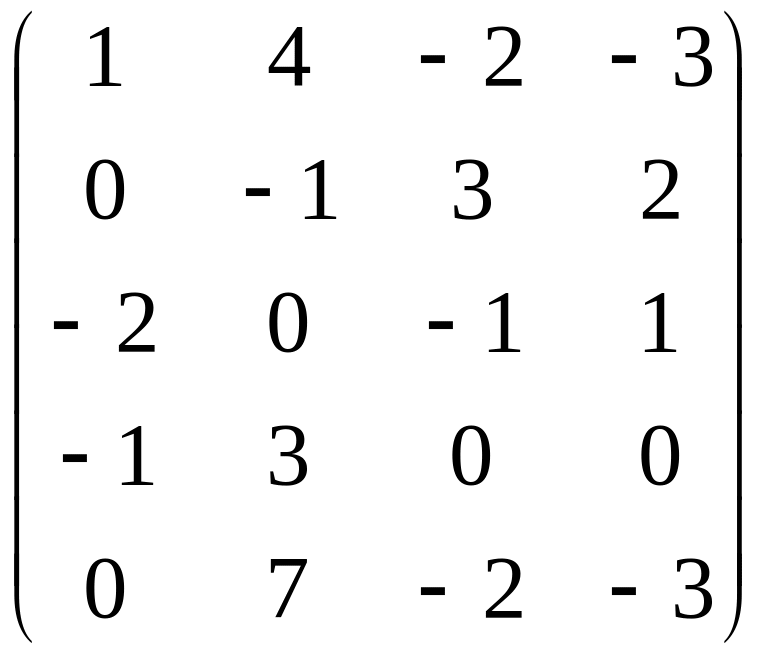
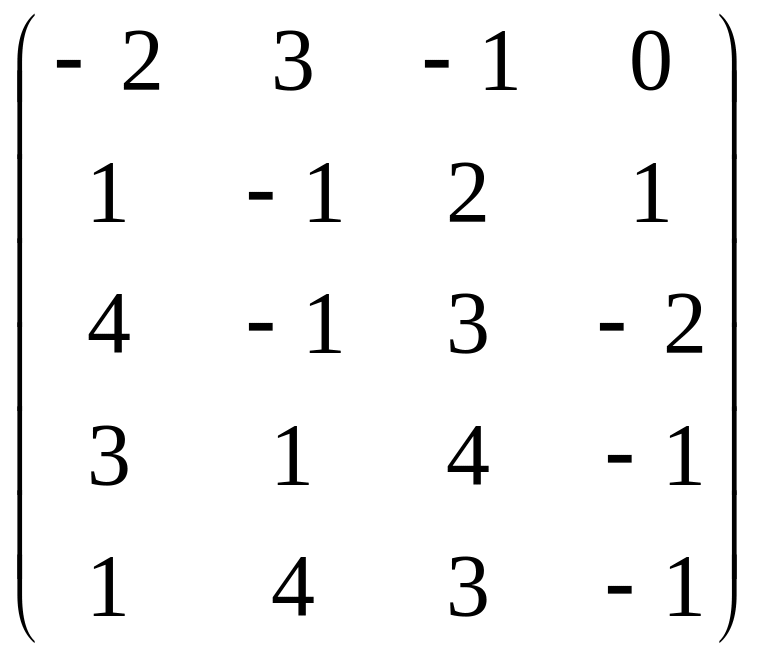
Вариант 9 Вариант 0
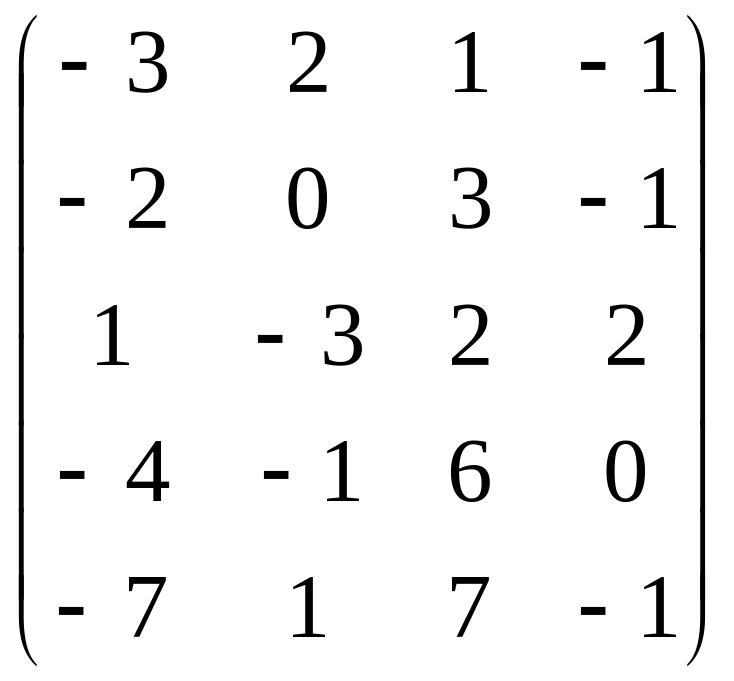
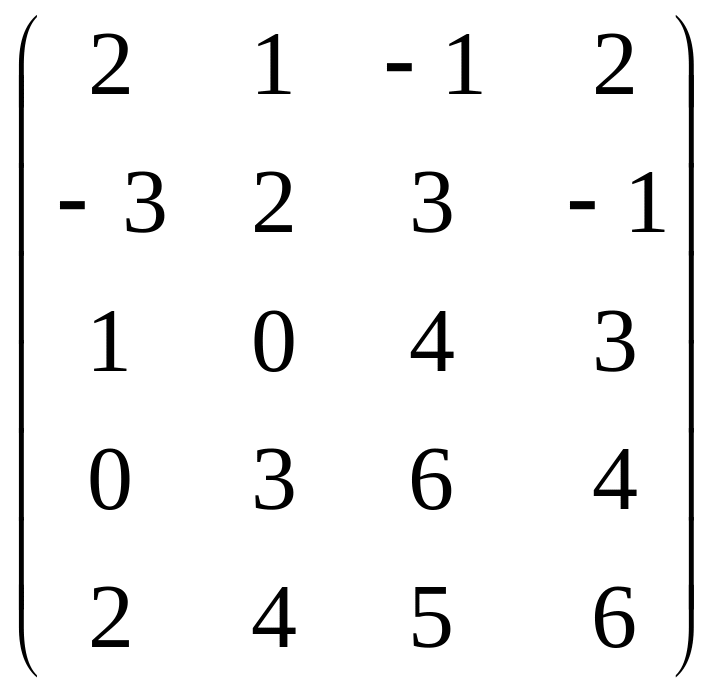
Решить систему методом Гаусса.
Вариант 1 Вариант 2
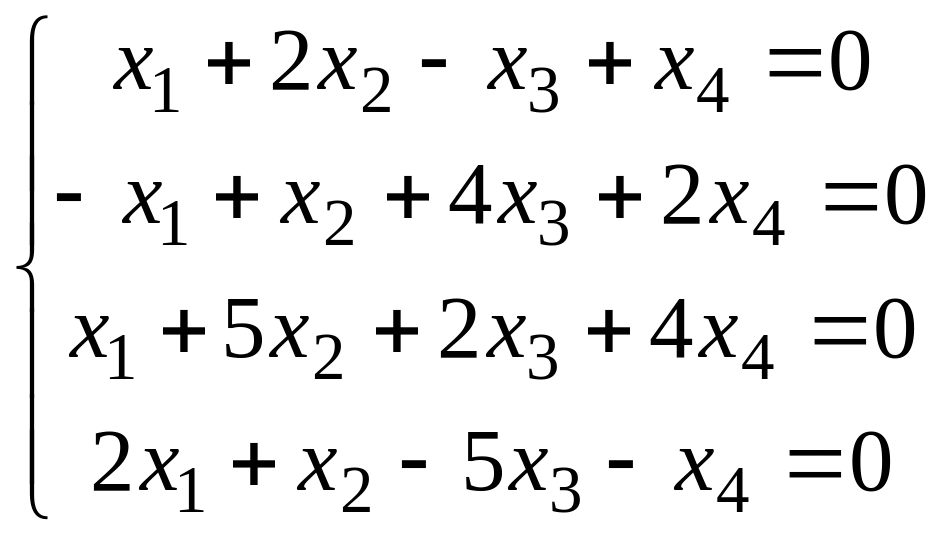
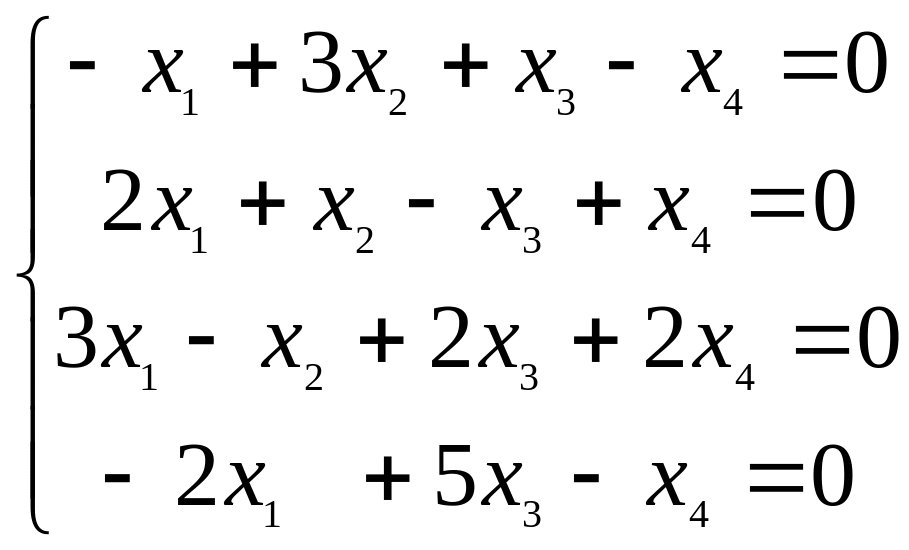
Вариант 3 Вариант 4
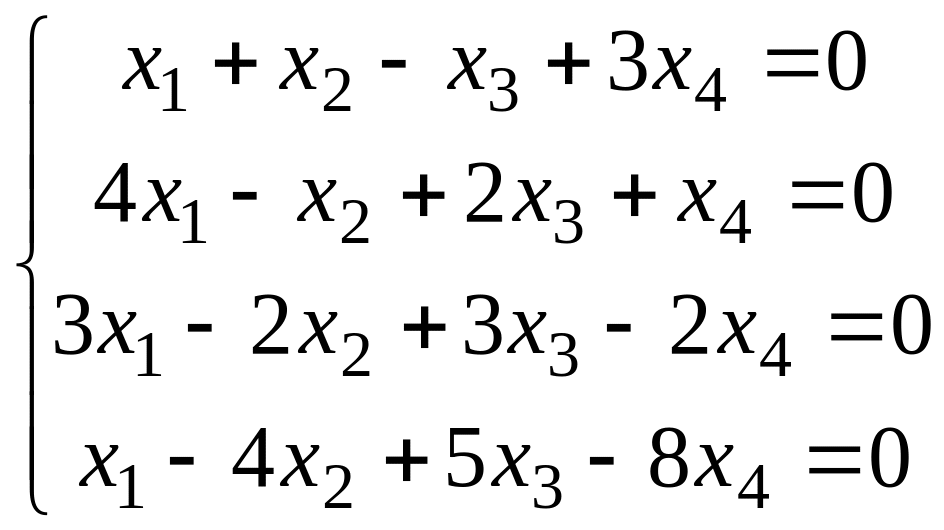
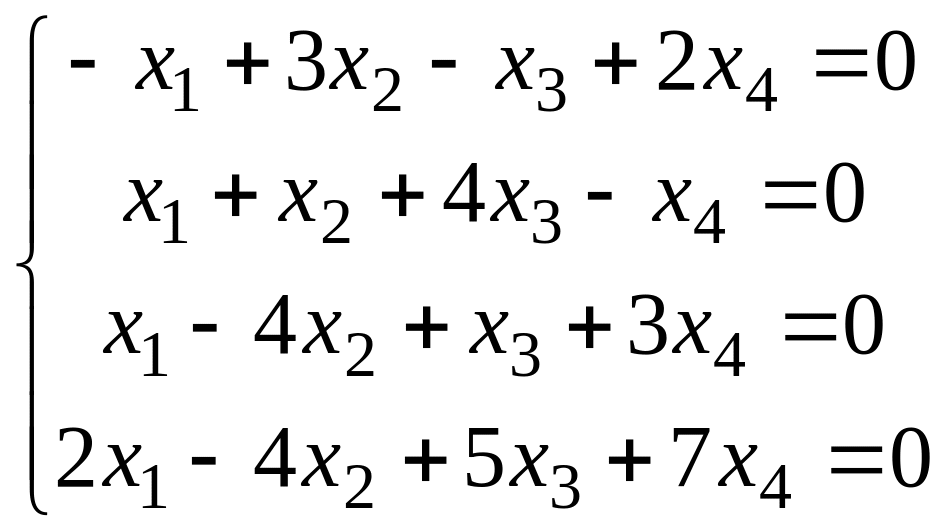
Вариант 5 Вариант 6
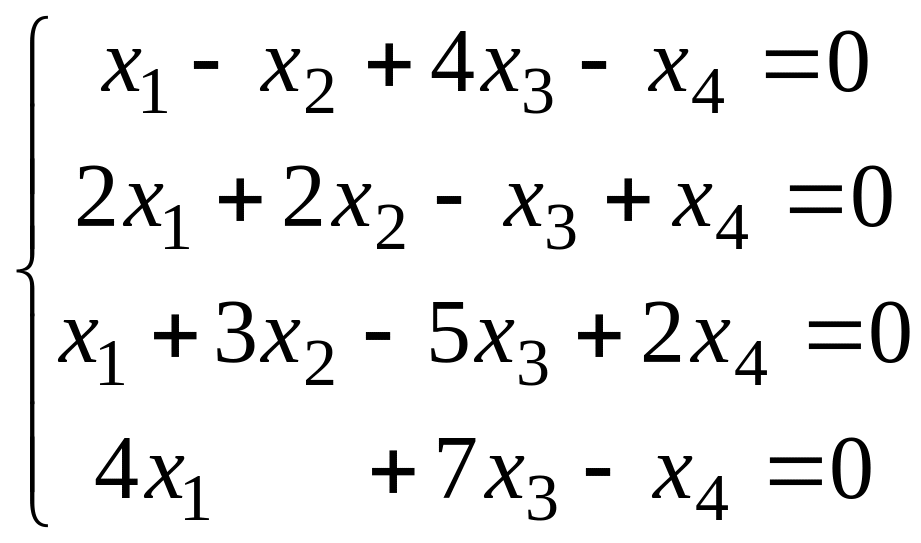
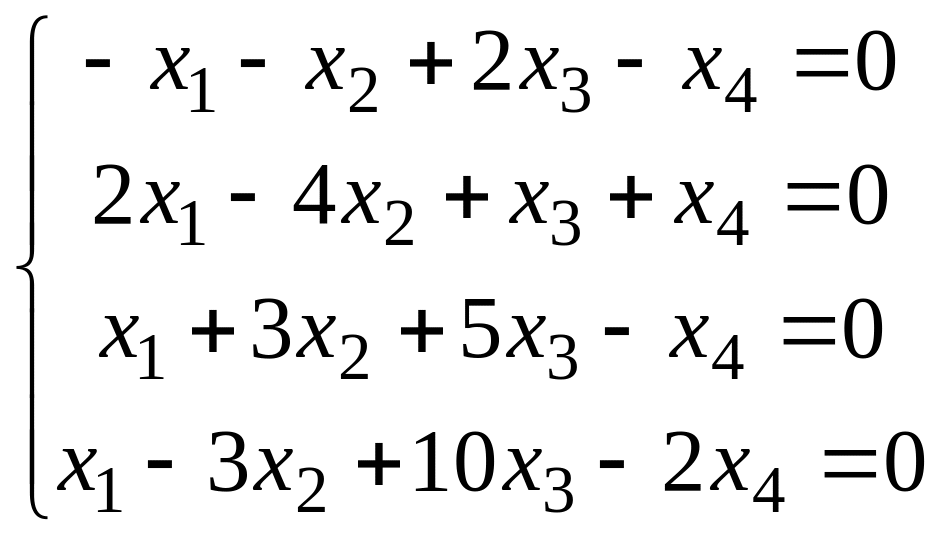
Вариант 7 Вариант 8
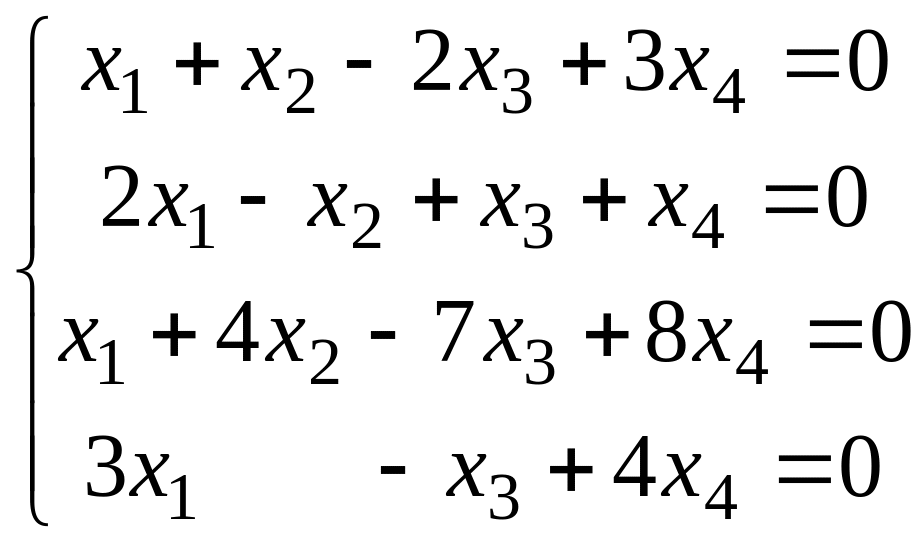
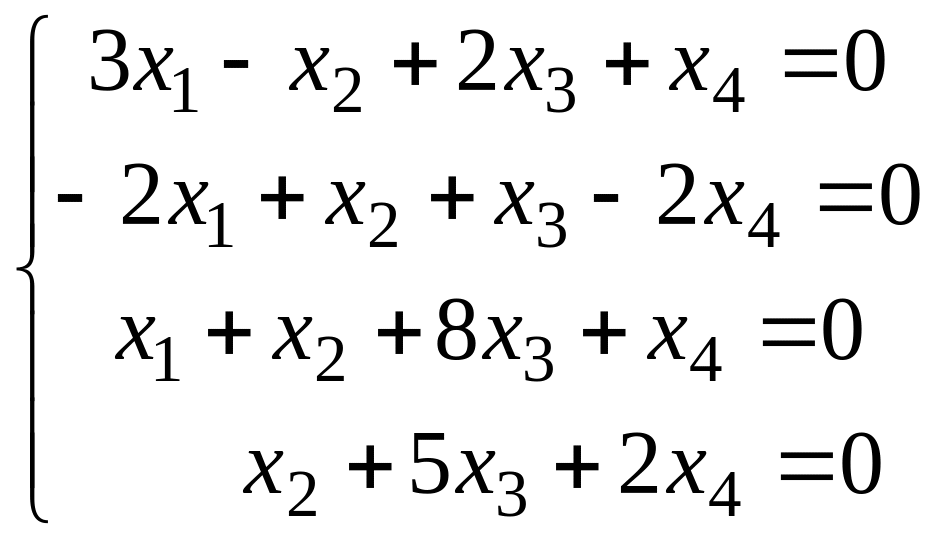
Вариант 9 Вариант 0
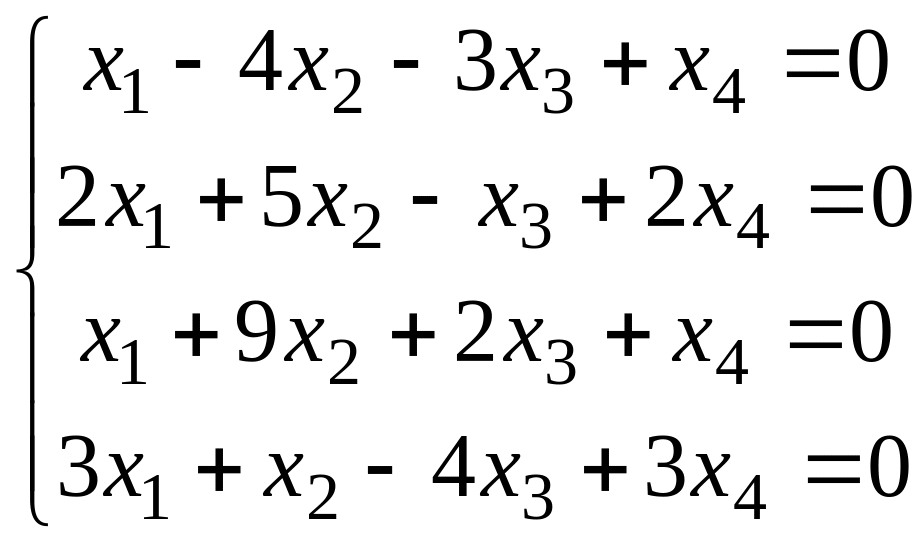
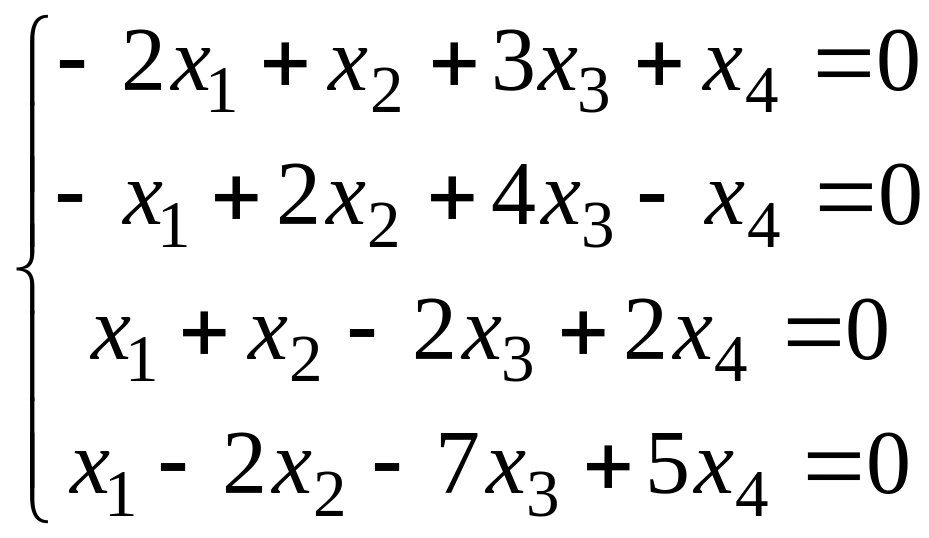
Найти собственные значения и собственные векторы матриц.
Вариант 1

Вариант 2

Вариант 3

Вариант 4

![]()
Вариант 5

Вариант 6

Вариант 7

Вариант 8

Вариант 9

Вариант 0

