Вычисление двойного интеграла.
Вычисление двойного
интеграла от функции
,
определённой в области D,
сводится к вычислению двукратного
интеграла вида
, (1)
если область D
(стандартная относительно оси Oy)
определяется условиями
,
или вида
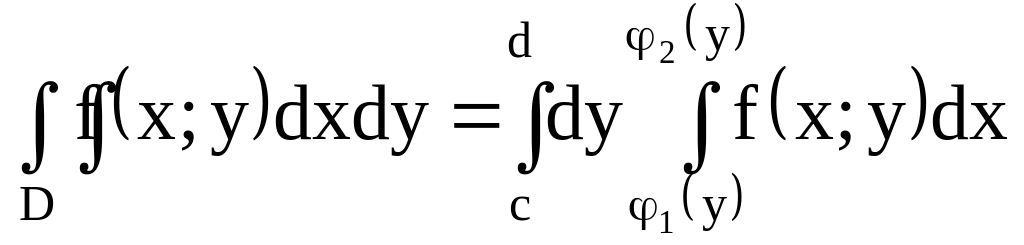, (2)
если область D
(стандартная относительно оси Ox)
определяется условиями
,
.
Переход от равенства (1) к (2) или обратно называется изменением порядка интегрирования.
Значение двойного интеграла не зависит от порядка интегрирования.
Заметим, что если
область D
не является стандартной ни относительно
оси Oy,
ни относительно оси Ox,
её разбивают на конечное число областей
(стандартных относительно оси Oy
(Ox))
и при вычислении двойного интеграла
по области D
используют свойство аддитивности.
Пример 1.
Изменить порядок
интегрирования
.
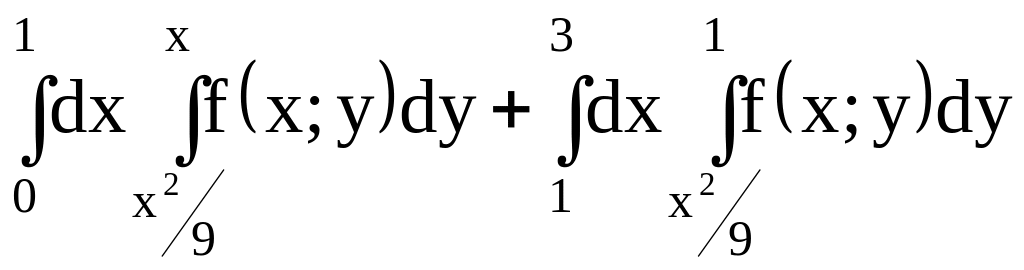З
ная
пределы интегрирования, найдём границы
областей интегрирования
и
каждого интеграла.
Область
ограничена линиями:
,
,
,
;
область
:
,
,
,
.
Построим области (рис. 1).
Изменим порядок
интегрирования, при этом объединим
области
и
в одну область D,
ограниченную слева и справа линиями
и
.
Постоянными пределами по у являются
числа 0 и 1. Тогда
Правую часть формул (1) и (2) называют повторным (двукратным) интегралом. Вычисление повторного интеграла следует начинать с вычисления внутреннего.
П
ример
2.
Вычислить двойной
интеграл
,
если область интегрирования
.
Построим область D (рис. 2).
Область интегрирования стандартная в направлении оси Oy, применим формулу (1):
Замена переменных в двойном интеграле.
Наряду с прямоугольной
системой координат на плоскости можно
использовать полярную систему координат.
Формулы, связывающие прямоугольные
координаты
и
с полярными
и
,
имеют вид:
(3)
Якобиан преобразования
в этом случае
и поэтому формула (1) принимает вид:
.
Для области D,
ограниченной лучами, образующими с
полярной осью углы
и
и кривыми
и
,
получаем
. (4)
Формулы (4) удобно использовать при решении задач, когда область D есть круг или сектор круга.
П
ример
3.
Вычислить двойной интеграл:
где
Область интегрирования
D
ограничена окружностью
с центром в точке
единичного радиуса (рис. 3). Следовательно,
удобно использовать формулы (4).
Согласно формулам
(3) уравнение окружности в полярных
координатах примет вид:
,
.
Геометрические приложения двойных интегралов.
Г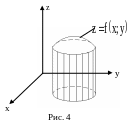
еометрический
смысл двойного интеграла заключается
в следующем: если
в области D,
то двойной интеграл
числено равен объёму цилиндрического
тела с основание D
и образующей, параллельной оси
,
которое ограничено сверху поверхностью
(рис. 4). В частном случае, когда
двойной интеграл равен площади области
D,
то есть
П
ример
4.
Вычислить площадь
фигуры, ограниченной линиями
,
Найдём координаты точек пересечения заданных линий, решая систему уравнений:
В результате
получим
и
.
Область D
ограничена прямой
и параболой
или
с вершиной в точке
(рис. 5).
Область является стандартной в направлении оси Ox, поэтому
