Математическая статистика

Задача 10. Обработка одномерной выборки (Вариант 88)

По выборке одномерной случайной величины:

- получить вариационный ряд;

- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F^*(x);

- построить гистограмму равноинтервальным способом;

- построить гистограмму равновероятностным способом;

- вычислить точечные оценки математического ожидания и дисперсии;

- вычислить интервальные оценки математического ожидания и дисперсии (γ = 0,95);

- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия ² и критерия Колмогорова ( = 0,05). График гипотетической функции распределения F₀(x) построить совместно с графиком F^*(x) в той же системе координат и на том же листе.

Необходимая для выполнения задачи выборка значений одномерной величины:

Одномерная выборка № 88:

2.97 -1.01 -1.82 -0.52 1.74 1.90 -2.89 0.30 1.75 1.70 -2.40 0.65 0.48 4.08 4.16 4.17 -3.15 0.87 -1.89 0.65 -2.58 0.52 1.86 -3.36 -1.05 4.79 -5.68 4.92 2.43 -5.37 -6.26 -1.11 1.74 0.33 0.12 -1.42 1.56 -4.41 -1.81 -1.79 1.76 -5.36 -3.00 -0.97 -2.09 4.94 2.34 -1.33 -0.53 2.14 -3.96 1.76 -3.60 -3.20 1.01 1.62 -1.25 2.56 0.85 -4.94 1.10 -4.22 1.10 -1.74 1.19 -0.28 -6.08 -5.30 -6.34 -0.43 -0.80 0.31 0.33 3.32 0.98 0.13 6.80 6.03 1.41 2.52 1.28 3.21 -3.45 -0.11 -2.63 -2.06 6.64 -1.63 0.13 -3.66 0.61 0.05 -3.55 2.25 -0.67 2.29 -1.04 -1.56 3.61 2.56

Решение.

№10,88

Вариационный ряд

-6,34	0,13
-6,26	0,30
-6,08	0,31
-5,68	0,33
-5,37	0,33
-5,36	0,48
-5,3	0,52
-4,94	0,61
-4,41	0,65
-4,22	0,65
-3,96	0,85
-3,66	0,87
-3,6	0,98
-3,55	1,01
-3,45	1,10
-3,36	1,10
-3,2	1,19
-3,15	1,28
-3	1,41
-2,89	1,56
-2,63	1,62
-2,58	1,70
-2,4	1,74
-2,09	1,74
-2,06	1,75
-1,89	1,76
-1,82	1,76
-1,81	1,86
-1,79	1,90
-1,74	2,14
-1,63	2,25
-1,56	2,29
-1,42	2,34
-1,33	2,43
-1,25	2,52
-1,11	2,56
-1,05	2,56
-1,04	2,97
-1,01	3,21
-0,97	3,32
-0,8	3,61
-0,67	4,08
-0,53	4,16
-0,52	4,17
-0,43	4,79
-0,28	4,92
-0,11	4,94
0,05	6,03
0,12	6,64
0,13	6,80

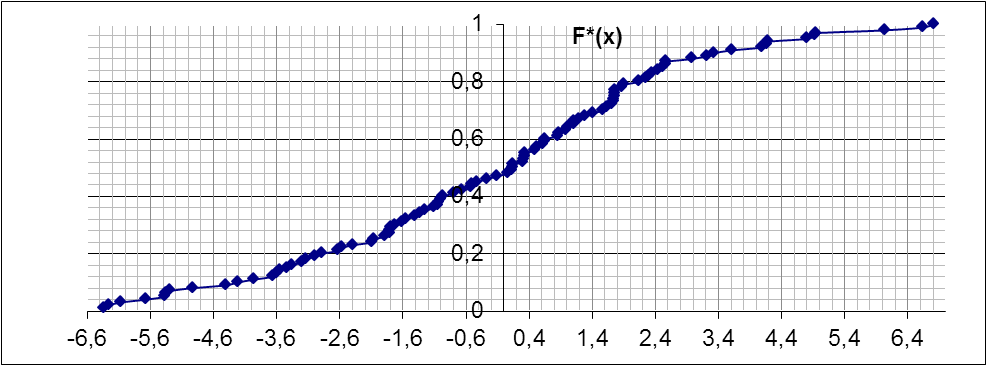
Эмпирическая функция распределения

По формуле 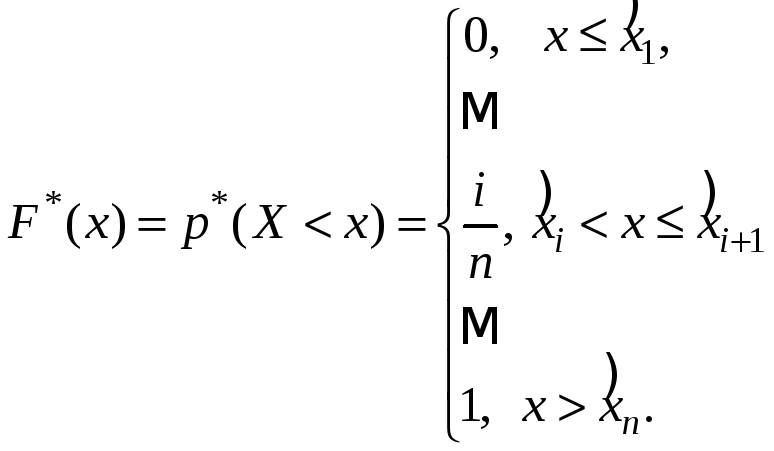построим график эмпирической функции распределения . Так как является неубывающей функцией и все ступеньки графика имеют одинаковую величину 1/n (или ей кратны – для одинаковых значений), то таблицу значений эмпирической функции распределения F*(x) можно не вычислять, а построить ее график непосредственно по и вариационному ряду, начиная с его первого значения

Количество интервалов M, необходимое для построения гистограмм, определим по объему выборки ( см. формулу (10.2)):

Для равноинтервальной гистограммы величины h_j, A_j, B_j, рассчитаем по формуле и заполним все колонки интервального статистического ряда :

Шаг интервала

h=

h=(6,8+6,34)/10=1,314

-6,340	-5,026	1,314	7	0,07	0,053	0,07
-5,026	-3,712	1,314	4	0,04	0,030	0,11
-3,712	-2,398	1,314	12	0,12	0,091	0,23
-2,398	-1,084	1,314	13	0,13	0,099	0,36
-1,084	0,230	1,314	15	0,15	0,114	0,51
0,230	1,544	1,314	18	0,18	0,137	0,69
1,544	2,858	1,314	18	0,18	0,137	0,87
2,858	4,172	1,314	7	0,07	0,053	0,94
4,172	5,486	1,314	3	0,03	0,023	0,97
5,486	6,800	1,314	3	0,03	0,023	1

Гистограмма равноинтервальным способом

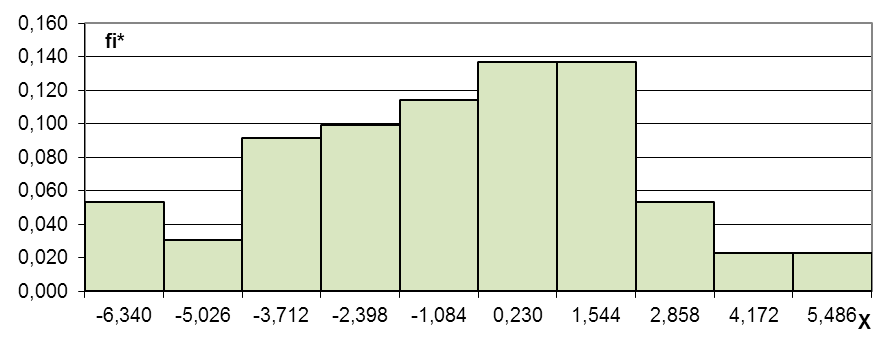
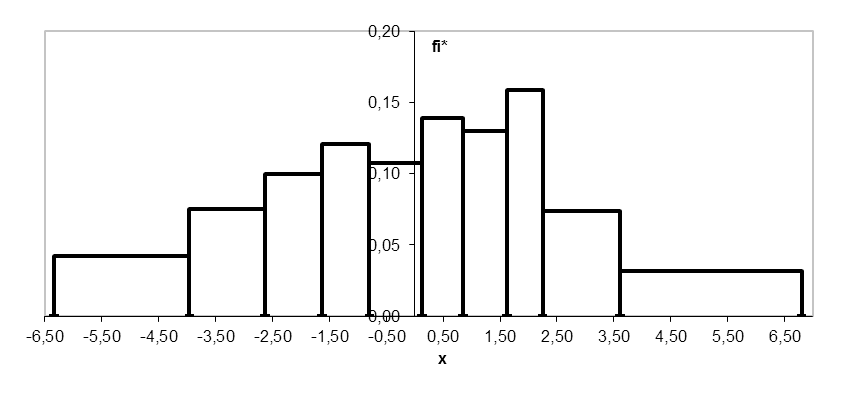
Гистограмма равновероятностным способом

-6,340	-5,026	2,38	10	0,1	0,042
-5,026	-3,712	1,33	10	0,1	0,075
-3,712	-2,398	1,00	10	0,1	0,100
-2,398	-1,084	0,83	10	0,1	0,120
-1,084	0,230	0,93	10	0,1	0,108
0,230	1,544	0,72	10	0,1	0,139
1,544	2,858	0,77	10	0,1	0,130
2,858	4,172	0,63	10	0,1	0,159
4,172	5,486	1,36	10	0,1	0,074
5,486	6,800	3,19	10	0,1	0,031

Вычислим точечную оценку математического ожидания по формуле:

.

Вычислим точечную оценку дисперсии по формуле:

.

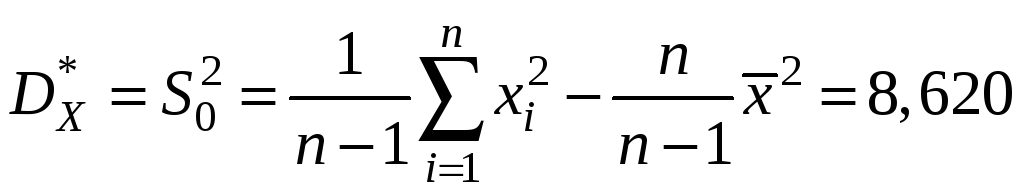Построим доверительный интервал для математического ожидания с надежностью γ = 0,95 по формуле .

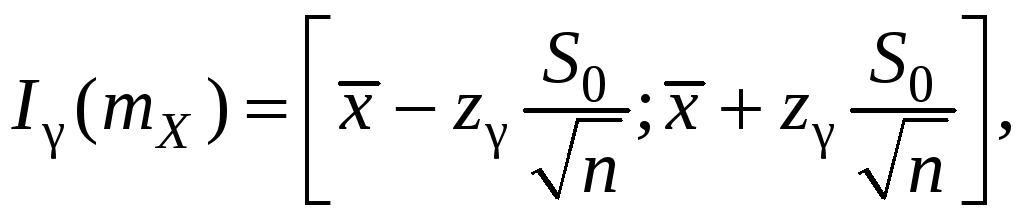Для этого в таблице функции Лапласа найдем значение, равное = 0,475, и определим значение аргумента, ему соответствующее: . Затем вычислим и получим доверительный интервал для математического ожидания:

.

Построим доверительный интервал для дисперсии с надежностью γ = 0,95 по формуле .

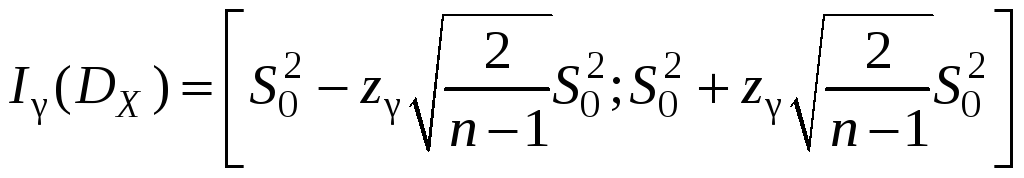Вычислим и получим доверительный интервал для дисперсии:

.

По виду гистограммы выдвинем гипотезу о нормальном распределении СВХ. Проверим гипотезу о нормальном распределении СВХ при помощи критерия χ²

Н₀: F(x)=F₀(x),

Н₁: F(x)≠F₀(x),

Где F₀(x), – теоретическая функция и плотность распределения

,

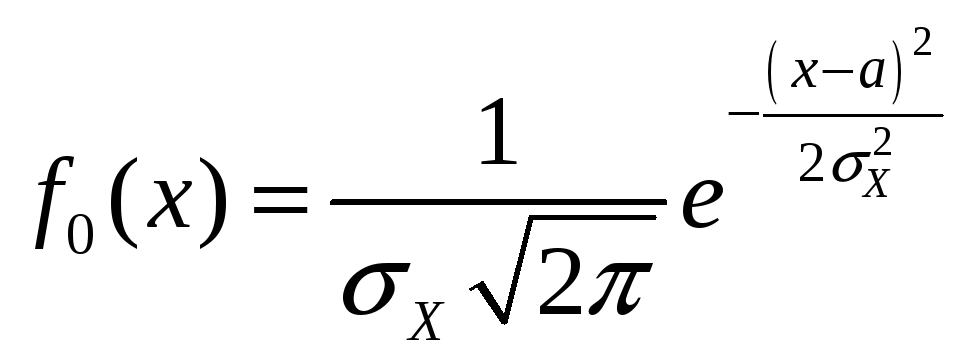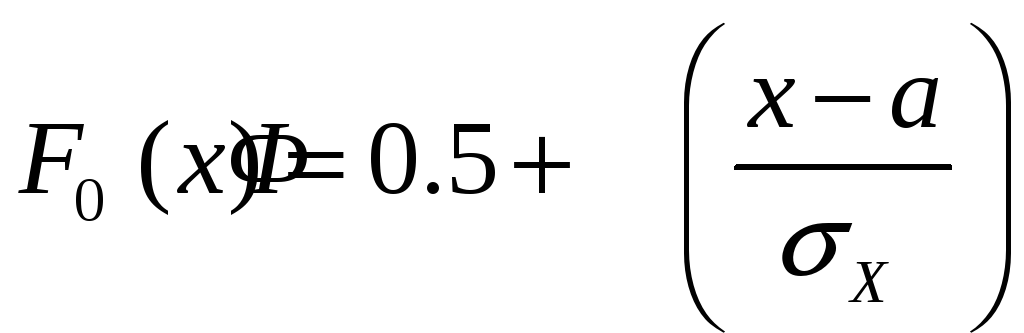
Где

,

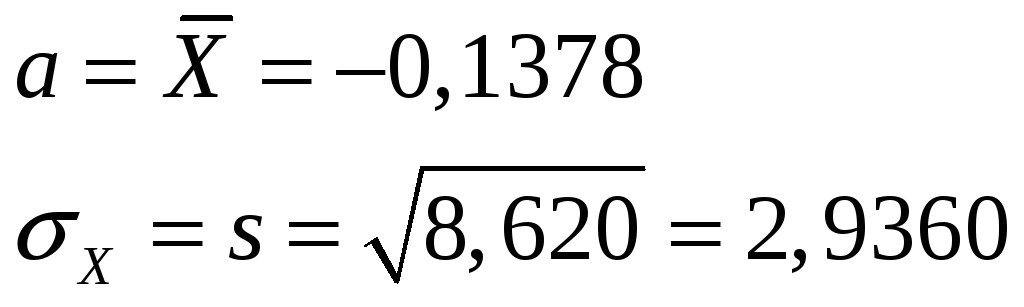
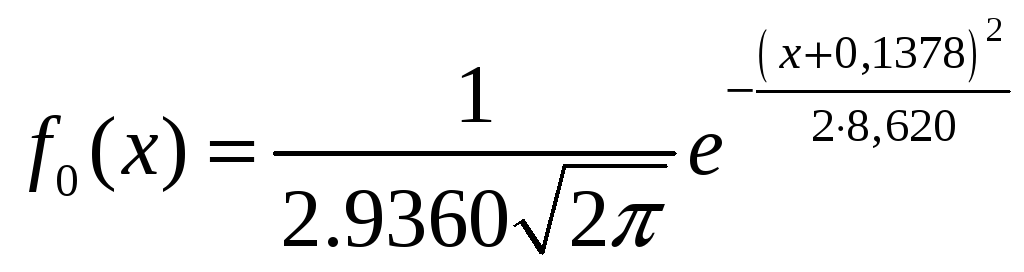χ²=

	-5,026	0	0,0441	0,0441	0,07	0,01525
-5,026	-3,712	0,0441	0,1056	0,0615	0,04	0,00751
-3,712	-2,398	0,1056	0,2131	0,1075	0,12	0,00145
-2,398	-1,084	0,2131	0,3665	0,1535	0,13	0,00359
-1,084	0,230	0,3665	0,5453	0,1787	0,15	0,00462
0,230	1,544	0,5453	0,7151	0,1699	0,18	0,00060
1,544	2,858	0,7151	0,8469	0,1318	0,18	0,01766
2,858	4,172	0,8469	0,9303	0,0834	0,07	0,00215
4,172	5,486	0,9303	0,9734	0,0431	0,03	0,00397
5,486		0,9734	1	0,0266	0,03	0,00042
			сумма	1	1	0,05722

χ²=100*0.057=5.7

По таблице найдем критическое значение критерия χ²_кр(7;0,05)=14,1, так как χ²_кр> χ² то гипотеза о нормальном распределении СВ Х принимается.

Проверим гипотезу о нормальном распределении СВ Х при помощи критерия Колмогорова

Н₀: F(x)=F₀(x)

Н₁: F(x)≠F₀(x)

Где F₀(x)– теоретическая функция распределения

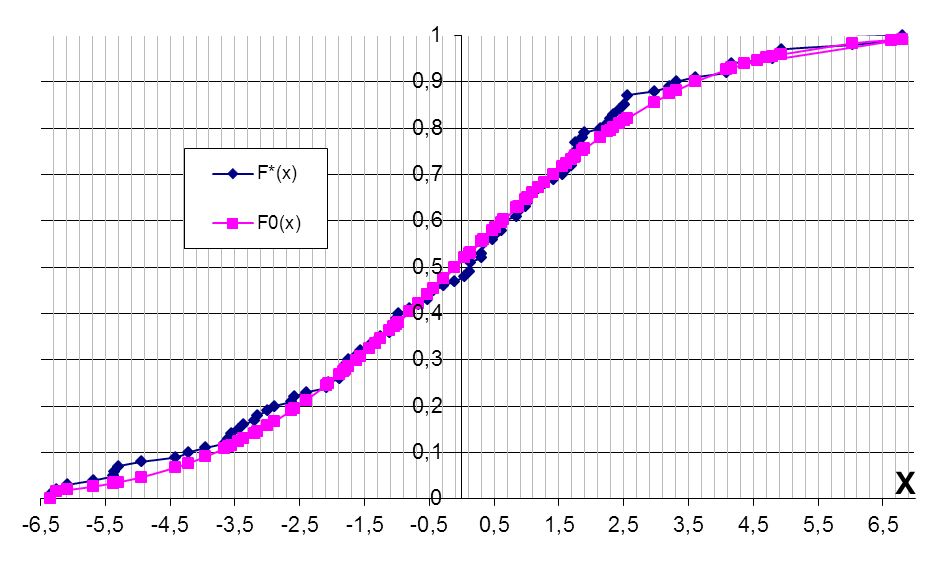
Вычислим значение критерия Колмогорова по формуле:

Из таблицы Колмогорова по заданному уровню значимости  =0,05 выбираем критическое значение

Так как , то гипотезу о нормальном законе распределения отвергать нет основания.

Задача 11. Обработка двухмерной выборки (Вариант 68)

По выборке двухмерной случайной величины:

- вычислить точечную оценку коэффициента корреляции;

- вычислить интервальную оценку коэффициента корреляции (γ = 0,95);

- проверить гипотезу об отсутствии корреляционной зависимости;

- вычислить оценки параметров a₀ и a₁ линии регрессии;

- построить диаграмму рассеивания и линию регрессии.

Необходимая для выполнения задачи выборка значений двухмерной величины (X, Y):

Двумерная выборка № 68:

( 4.03; 6.42) ( 4.35; 3.21) ( 2.69; 3.67) ( 5.44; 7.52) ( 3.73; 5.37) ( 2.85; 3.47) ( 1.78; 4.58) ( 3.44; 4.44) ( 3.79; 4.46) ( 3.32; 4.62) ( 2.97; 3.60) ( 2.85; 4.35) ( 4.40; 4.53) ( 3.38; 5.00) ( 2.14; 3.99) ( 1.57; 3.68) ( 1.37; 4.95) ( 2.46; 2.34) ( 3.11; 4.07) ( 3.49; 4.18) ( 3.66; 4.14) ( 2.43; 3.95) ( 3.22; 3.87) ( 3.82; 5.87) ( 2.77; 4.61) ( 2.56; 3.47) ( 3.01; 4.38) ( 4.45; 5.28) ( 4.16; 5.47) ( 3.20; 4.82) ( 4.37; 5.94) ( 3.60; 6.15) ( 4.77; 7.29) ( 1.58; 3.91) ( 2.13; 2.48) ( 3.75; 5.08) ( 1.12; 3.23) ( 3.54; 5.78) ( 2.97; 5.57) ( 4.19; 4.86) ( 4.58; 5.69) ( 2.40; 3.72) ( 4.28; 5.10) ( 5.56; 5.97) ( 4.20; 4.79) ( 1.79; 4.96) ( 4.19; 5.39) ( 3.53; 4.24) ( 3.75; 4.69) ( 4.21; 5.49)

Решение.

№11,68

Состоятельная оценка коэффициента корреляции

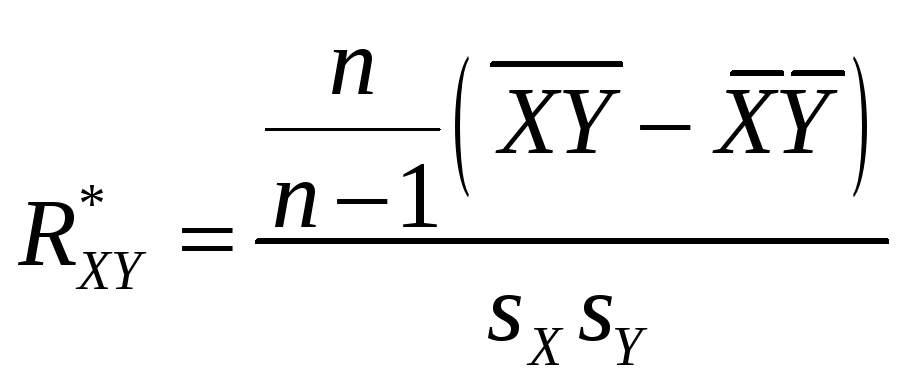
Расчетная таблица

	X	Y	X*Y	X2	Y2
	4,03	6,42	25,8726	16,2409	41,2164
	4,35	3,21	13,9635	18,9225	10,3041
	2,69	3,67	9,8723	7,2361	13,4689
	5,44	7,52	40,9088	29,5936	56,5504
	3,73	5,37	20,0301	13,9129	28,8369
	2,85	3,47	9,8895	8,1225	12,0409
	1,78	4,58	8,1524	3,1684	20,9764
	3,44	4,44	15,2736	11,8336	19,7136
	3,79	4,46	16,9034	14,3641	19,8916
	3,32	4,62	15,3384	11,0224	21,3444
	2,97	3,6	10,692	8,8209	12,96
	2,85	4,35	12,3975	8,1225	18,9225
	4,4	4,53	19,932	19,36	20,5209
	3,38	5	16,9	11,4244	25
	2,14	3,99	8,5386	4,5796	15,9201
	1,57	3,68	5,7776	2,4649	13,5424
	1,37	4,95	6,7815	1,8769	24,5025
	2,46	2,34	5,7564	6,0516	5,4756
	3,11	4,07	12,6577	9,6721	16,5649
	3,49	4,18	14,5882	12,1801	17,4724
	3,66	4,14	15,1524	13,3956	17,1396
	2,43	3,95	9,5985	5,9049	15,6025
	3,22	3,87	12,4614	10,3684	14,9769
	3,82	5,87	22,4234	14,5924	34,4569
	2,77	4,61	12,7697	7,6729	21,2521
	2,56	3,47	8,8832	6,5536	12,0409
	3,01	4,38	13,1838	9,0601	19,1844
	4,45	5,28	23,496	19,8025	27,8784
	4,16	5,47	22,7552	17,3056	29,9209
	3,2	4,82	15,424	10,24	23,2324
	4,37	5,94	25,9578	19,0969	35,2836
	3,6	6,15	22,14	12,96	37,8225
	4,77	7,29	34,7733	22,7529	53,1441
	1,58	3,91	6,1778	2,4964	15,2881
	2,13	2,48	5,2824	4,5369	6,1504
	3,75	5,08	19,05	14,0625	25,8064
	1,12	3,23	3,6176	1,2544	10,4329
	3,54	5,78	20,4612	12,5316	33,4084
	2,97	5,57	16,5429	8,8209	31,0249
	4,19	4,86	20,3634	17,5561	23,6196
	4,58	5,69	26,0602	20,9764	32,3761
	2,4	3,72	8,928	5,76	13,8384
	4,28	5,1	21,828	18,3184	26,01
	5,56	5,97	33,1932	30,9136	35,6409
	4,2	4,79	20,118	17,64	22,9441
	1,79	4,96	8,8784	3,2041	24,6016
	4,19	5,39	22,5841	17,5561	29,0521
	3,53	4,24	14,9672	12,4609	17,9776
	3,75	4,69	17,5875	14,0625	21,9961
	4,21	5,49	23,1129	17,7241	30,1401
сумма	166,95	234,64	818,00	608,55	1157,47
среднее	3,3390	4,6928	16,3600	12,1710	23,1494