5 Численные методы решения уравнений

Покажем, как можно решить изначальную систему уравнений, не прибегая к оптимизационным методам. В случае, если наша система представляет собой СЛАУ, целесообразно прибегнуть к таким методам, как метод Гаусса или метод Ричардсона. Однако мы всё же будем исходить из предположения, что вид функции нам неизвестен и воспользуемся одним из итерационных методов численного решения. Среди большого разнообразия таковых выберем один из наиболее известных — метод Ньютона. Этот метод в свою очередь основывается на принципах метода простой итерации. Поэтому сначала будет изложена суть последнего.

[править]

Метод простой итерации

В основе метода заложено понятие сжимающего отображения. Определим терминологию:

Говорят, что функция осуществляет сжимающее отображение на , если

Тогда основная теорема будет выглядеть так: Теорема Банаха (принцип сжимающих отображений).

Если — сжимающее отображение на , то:

у — корень;

итерационная последовательность сходится к этому корню;

для очередного члена справедливо .

Поясним смысл параметра . Согласно теореме Лагранжа имеем:

Отсюда следует, что . Таким образом, для сходимости метода достаточно, чтобы

.........

и так далее, пока

[править]

Применительно к СЛАУ

Рассмотрим систему:

Для неё итерационное вычисление будет выглядеть так:

Сходимость метода будет осуществлять

Следует отметить, что для оценки сходимости вычисляется не определитель матрицы, а норма матрицы. Поэтому в данном случае поставлены двойные вертикальные черты, а не одинарные.

[править]

Алгоритм

Условие преобразуется к виду , где — сжимающая

Задаётся начальное приближение и точность

Вычисляется очередная итерация

Если , то и возврат к шагу 3.

Иначе и остановка.

6 Метод итераций. Одним из наиболее важных способов численного решения уравнений является метод итерации. Сущность этого метода заключается в следующем. Пусть дано уравнение

f(x)=0.

(1)

где f(x) – непрерывная функция, и требуется определить его вещественные корни. Заменим уравнение (1) равносильным уравнением

x=j (x).

(2)

Выберем каким-либо способом грубо приближенное значение корня x0 и подставим его в правую часть уравнения (2). Тогда получим некоторое число

x1=j (x0).

(3)

Подставляя теперь в правую часть равенства (3) вместо x0 число x1 получим новое число x2=j (x1). Повторяя этот процесс, будем иметь последовательность чисел

xn=j (xn-1) (n=1, 2,...).

(4)

Если эта последовательность – сходящаяся, т.е. существует предел ,

то, переходя к пределу в равенстве (4) и предполагая функцию j (x) непрерывной, найдем: или

x =j (x). (5)

Таким образом, предел x является корнем уравнения (2) и может быть вычислен по формуле (4) с любой степенью точности.

Доказано, что достаточными условиями сходимости итерационного процесса является выполнение условия | j (x)<1 для xО [a, ,b].

При этом процесс сходится к единственному корню x .

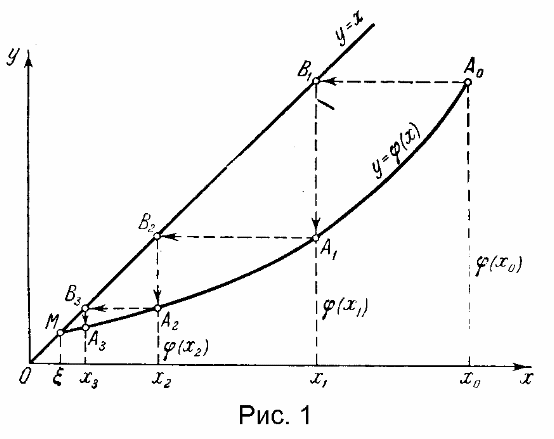
На рис. 1 приведен пример сходящегося итерационного процесса xn+1=j (xn) при 0<j ’(x)<1 и на рис.2 – расходящегося при j ’(x)<1.

\

6 Операции над множествами

Материал из Википедии — свободной энциклопедии

Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые.Содержание [убрать]

1 Сравнение множеств

2 Операции над множествами

2.1 Бинарные операции

2.2 Унарные операции

3 Приоритет выполнения операций

Сравнение множеств

Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент B:

В этом случае A называется подмножеством B, B — надмножеством A. Если

и

, то A называется собственным подмножеством B. Заметим, что

. По определению .

Два множества называются равными, если они являются подмножествами друг друга:

Иногда для того, чтобы подчеркнуть, что множества могут быть равны, используется запись:

Операции над множествами

Бинарные операции

Ниже перечислены основные операции над множествами:

пересечение:

объединение:

Если множества A и B не пересекаются:

, то их объединение обозначают также: .

разность (дополнение):

симметрическая разность:

Декартово или прямое произведение:

Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.

Унарные операции

Абсолютное дополнение:

Операция дополнения подразумевает некоторый универсум (универсальное множество U, которое содержит A):

Относительным же дополнением называется А\В (см.выше):

Мощность множества:

| A |

Результатом является кардинальное число (для конечных множеств — натуральное).

Множество всех подмножеств (булеан):

Обозначение происходит из того, что в случае конечных множеств.

Приоритет выполнения операций

Сначала выполняются операции дополнения, затем пересечения, объединения и разности, которые имеют одинаковый приоритет. Последовательность выполнения операций может быть изменена скобками.

7 Формула Симпсона (также Ньютона-Симпсона[1]) относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761). Суть приёма заключается в приближении подынтегральной функции на отрезке интерполяционным многочленом второй степени , то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.

Формула

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a,b]:

где f(a), f((a + b) / 2) и f(b) — значения функции в соответствующих точках (на концах отрезка и в его середине).

Погрешность

При условии, что у функции f(x) на отрезке [a,b] существует четвёртая производная, погрешность E(f), согласно найденной Джузеппе Пеано формуле равна:

В связи с тем, что значение ζ зачастую неизвестно, для оценки погрешности используется следующее неравенство:

9 Применение формулы Тейлора при вычислении предела функции

Формула Тейлора

Формулы Тейлора часто применяют для приближенного вычисления значений функции и о(хn) указывает степень точности вычисления.

Чтобы пользоваться формулой Тейлора, надо знать вид формулы Тейлора для основных элементарных функций:

Тейлора формула

Тейлора формула, формула

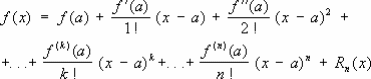
изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n [то есть Rn (x) = an (x)(x—a) n, где an (x) ® 0 при х ® а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x)можно представить в видах:

,

где x и x1 — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.