Дослідження операцій

1. Загальна задача лп. Допустима область та її властивості. Поняття вершини допустимої області, базисного (опорного) плану задачі.

http://bibl.kma.mk.ua/pdf/posibnuku/226/5.pdf

2. Стандартна задача лп. Зведення загальної задачі до стандартної. Канонічна задача лп. Зведення стандартної задачі до канонічної.

Математична модель загальної задачі лінійного програмування має вигляд:

(1)

(2)

(3)

Область, яка визначається співвідношеннями (2) і (3) називається допустимою областю значень D або допустимим многогранником (обмеженим чи необмеженим). Область D може бути порожньою, непорожньою обмеженою або непорожньою необмеженою. Область D, якщо вона непорожня, може містити скінчену кількість планів лише у випадку коли цей план єдиний. В усіх інших випадках множина D має потужність континум. Якщо області D належать хочаб дві точки, то цій області належить весь відрізок, який ці точки з’єднує. Якщо область D має вершини та існує розв’язок задачі лінійного програмування, то розв’язком є координати хоча б однієї вершини. Якщо розв’язок досягається в двох вершинах, то розв’язок буде досягатися на всьому відрізку, який з’єднує ці вершини.

Якщо точка задовольняє умови (2) і (3), то її називають допустимою точкою або планом задачі. Якщо точка задовольняє умову , то її називають оптимальною точкою або оптимальним планом задачі.

У випадку коли область допустимих значень необмежена, то не завжди буде досягатися мінімальне або максимальне значення. Задача лінійного програмування може мати багато розв’язків або може не мати жодного, може бути і єдиний розв’язок. Розв’язок задачі на max (min) існує тоді і тільки тоді, коли лінійна форма (цільова функція) обмежена зверху (знизу) на області допустимих значень.

Математична модель стандартної задачі лінійного програмування має вигляд:

(1)

(2)

(3)

Алгоритм переходу від ЗЗЛП до СЗЛП.

Переходу від загальної задачі лінійного програмування до стандартної задачі лінійного програмування здійснюється просто.

• Якщо в задачі лінійного програмування йде мова про максимізацію лінійної форми (цільової функції), то достатньо розглядати лінійну форму з протилежним знаком: .

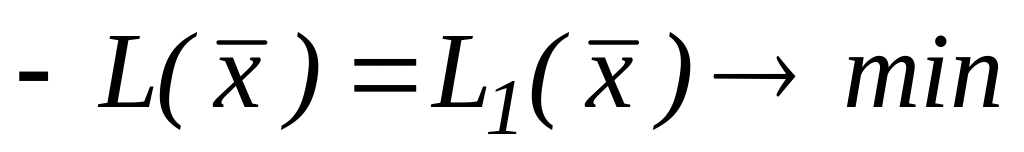• Якщо в умовах, які накладаються на змінні, присутні нерівності типу: для деякого і, то легко перейти до рівності, ввівши додаткову (нову) змінну 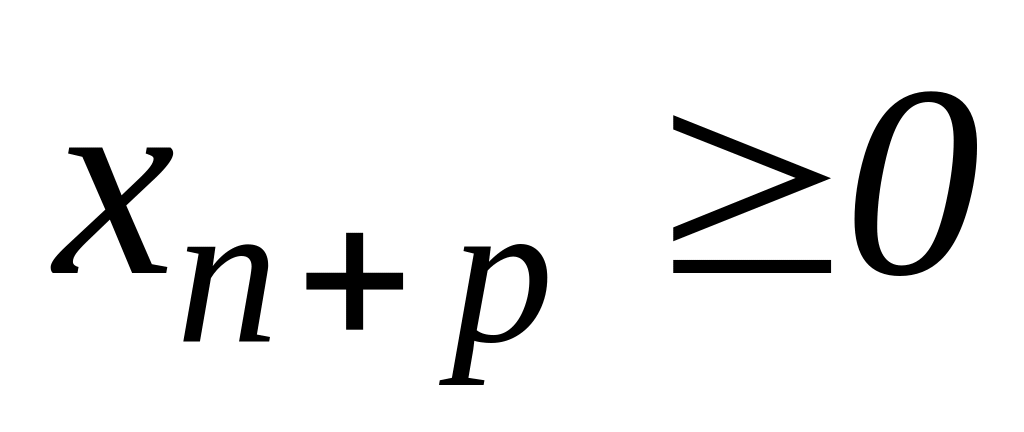таким чином: .

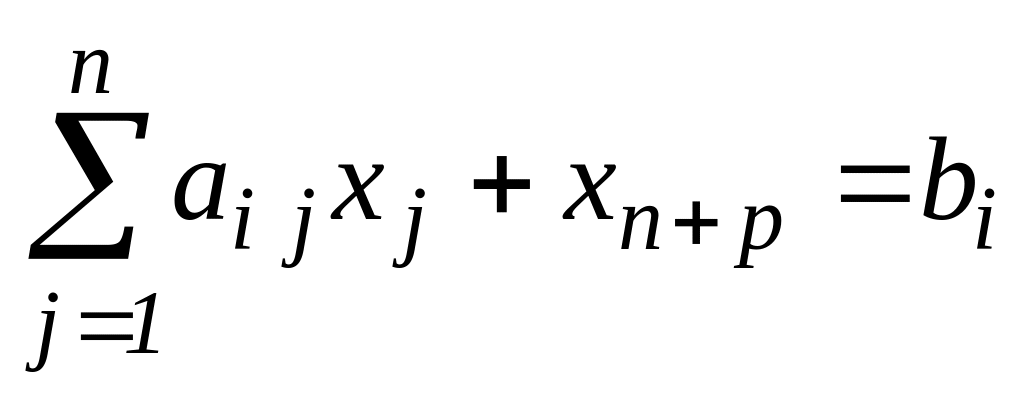• Якщо в умовах, які накладаються на змінні, присутні нерівності типу: 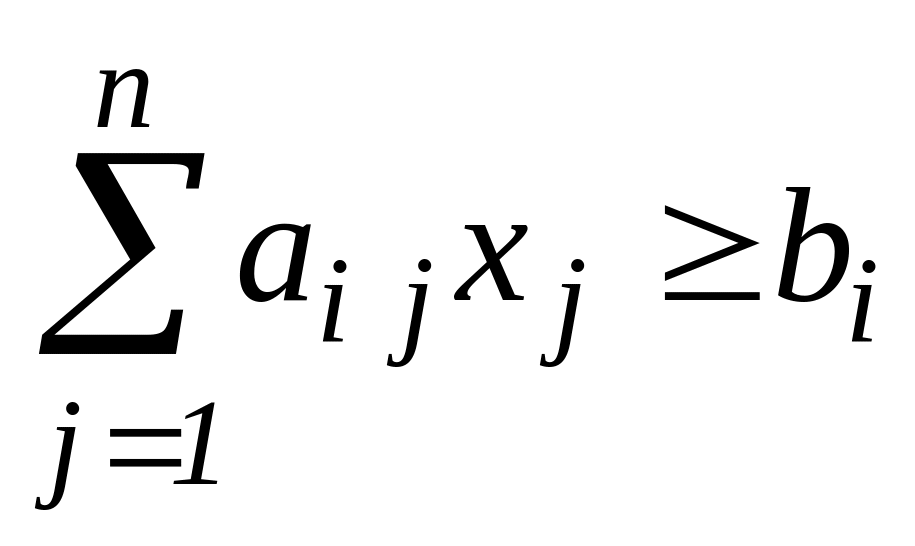для деякого і, то легко перейти до рівності, ввівши додаткову (нову) змінну таким чином: .

Зауваження. Очевидно, що при введені додаткових змінних збільшується розмірність задачі.

• Якщо при деякому j змінна 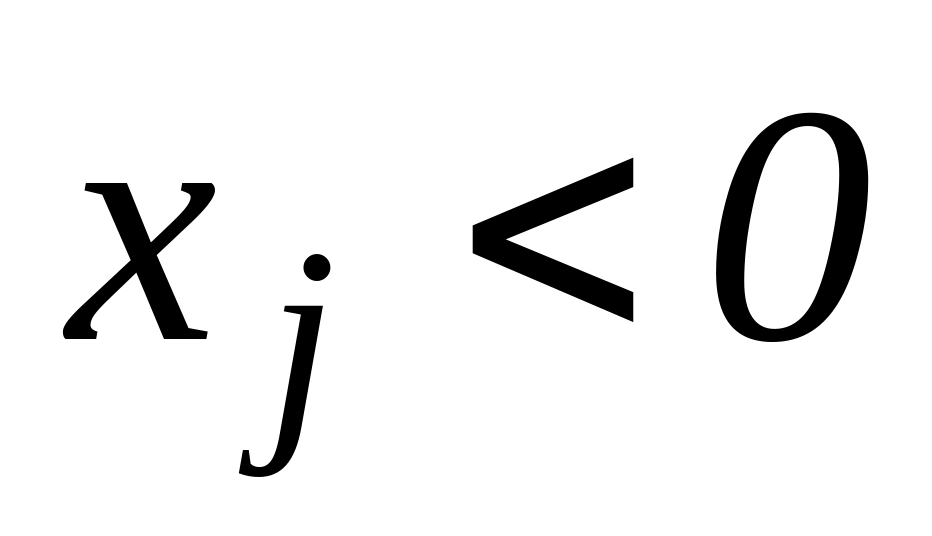, то її можна представити у вигляді двох невід’ємних змінних: , де .

Загальний вигляд канонічної задачі:

Канонічна задача лінійного програмування в матричній формі має вигляд:

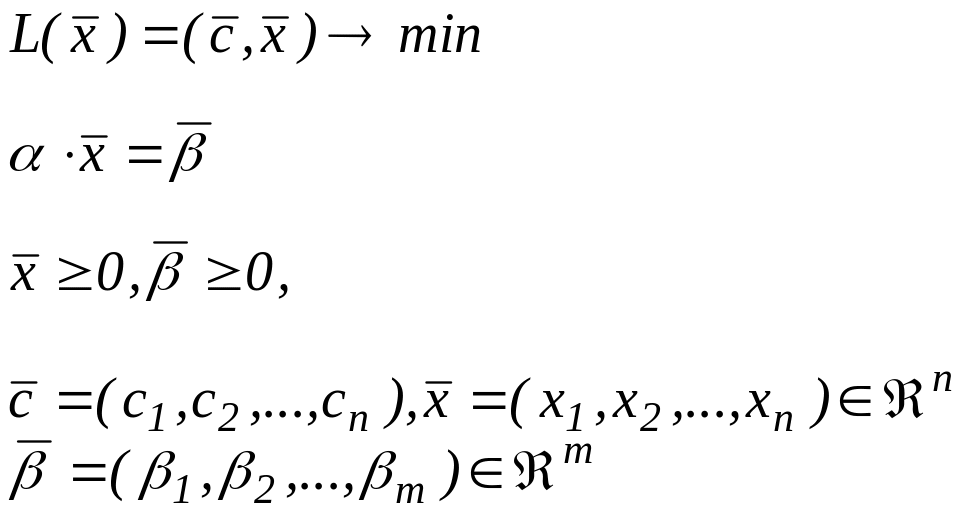
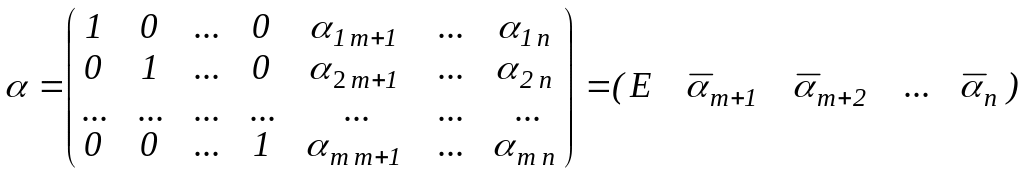
Для такої задачі лінійного програмування можна зразу вказати один із опорних планів. Оптимальним планом є такий вектор: . Цей вектор задовольняє умови (2) і (3). Крім того, m першим компонентам відповідає лінійно-незалежна система векторів.

Розглянемо теоретичну можливість переходу від стандартної задачі лінійного програмування до канонічної.

Нехай якому відповідає базисна матриця . Помножимо на зліва. Отримаємо , тоді будемо мати такий вигляд , крім того .

Критерій оптимальності. Якщо існує базисний розв’язок канонічної задачі лінійного програмування і , то – оптимальний план задачі. Де – відносна оцінка, яка обчислюється по формулі , причому відносні оцінки для базисних змінних рівні нулю.

Ознака необмеженості цільової функції знизу. Якщо серед відносних оцінок деякого базисного плану задачі лінійного програмування існує від’ємна ( ), а серед компонент k-ого стовпчика немає додатних коефіцієнтів ( ), то лінійна форма (цільова функція) – необмежена знизу на допустимій множині.

Для розв’язання канонічної задачі лінійного програмування застосовуємо симплекс-метод.