
Первый закон термодинамики
Первый закон термодинамики (закон сохранения энергии для тепловых процессов) определяет количественное соотношение между изменением внутренней энергии системы дельта U, количеством теплоты Q, подведенным к ней, и суммарной работой внешних сил A, действующих на систему.
Первый закон термодинамики - Изменение внутренней энергии системы при ее переходе из одного состояния в другое равно сумме количества теплоты, подведенного к системе извне, и работы внешних сил, действующих на нее:
![]()
Первый закон термодинамики - количество теплоты, подведенное к системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами:
![]()
Коэффициент полезного действия (КПД) тепловой машины
h=A/Qнагр= (Qнагр - |Qхолод|)/Qнагр=1-|Qхолод|/Qнагр.\
* 2-й закон — второе начало термодинамики: Второй закон термодинамики исключает возможность создания вечного двигателя второго рода. Имеется несколько различных, но в то же время эквивалентных формулировок этого закона. 1 — Постулат Клаузиуса. Процесс, при котором не происходит других изменений, кроме передачи теплоты от горячего тела к холодному, является необратимым, то есть теплота не может перейти от холодного тела к горячему без каких либо других изменений в системе. Это явление называют рассеиванием или дисперсией энергии. 2 — Постулат Кельвина. Процесс, при котором работа переходит в теплоту без каких либо других изменений в системе, является необратимым, то есть невозможно превратить в работу всю теплоту, взятую от источника с однородной температурой, не проводя других изменений в системе.
3. Закон Кулона: сила взаимодействия двух точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними. |q1||q2| F=k —————. r2
закон Кулона можно записать в векторном виде: ® q1q2 ® F12=k————— r12. r12
4.
Поток
вектора напряженности электростатического
поля
![]() через
произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
расположенных внутри этой поверхности,
деленной на электрическую постоянную
ε0.
через
произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
расположенных внутри этой поверхности,
деленной на электрическую постоянную
ε0.
|
5. Связь между напряженностью электрического поля и потенциалом
Как известно, в потенциальном поле сила может быть получена из потенциальной энергии из соотношения
![]() (1.17)
(1.17)
Тогда для напряженности электрического поля из соотношений

Получается
![]() (1.18)
(1.18)
С другой стороны, из соотношений (1.8) и (1.14) следует, что
 (1.19)
(1.19)
Поверхности
равного потенциала, т.е. такие поверхности,
на которых
![]() называются
эквипотенциальными.
называются
эквипотенциальными.
6.
.
Ёмкость
плоского конденсатора, состоящего из
двух параллельных металлических пластин
площадью
![]() каждая,
расположенных на расстоянии
каждая,
расположенных на расстоянии
![]() друг
от друга, в системе СИ
выражается формулой:
друг
от друга, в системе СИ
выражается формулой:
![]() ,
где
,
где
![]() —
относительная
диэлектрическая проницаемость
среды, заполняющей пространство между
пластинами (в вакууме равна единица),
—
относительная
диэлектрическая проницаемость
среды, заполняющей пространство между
пластинами (в вакууме равна единица),
![]() —
электрическая постоянная, численно
равная
—
электрическая постоянная, численно
равная
![]() (эта
формула справедлива, лишь когда
много
меньше линейных размеров пластин).
(эта
формула справедлива, лишь когда
много
меньше линейных размеров пластин).
7.
8. На практике конденсаторы часто соединяют в батареи - последовательно или параллельно.
П ри
параллельном соединении напряжение на
всех обкладках одинаковое
U1
= U2
= U3
= U = e, а емкость батареи равняется сумме
емкостей отдельных конденсаторов C = C1
+ C2
+ C3.
ри
параллельном соединении напряжение на
всех обкладках одинаковое
U1
= U2
= U3
= U = e, а емкость батареи равняется сумме
емкостей отдельных конденсаторов C = C1
+ C2
+ C3.
П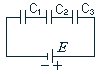 ри
последовательном соединении заряд на
обкладках всех конденсаторов одинаков
Q1
= Q2
= Q3,
а напряжение батареи равняется сумме
напряжений отдельных конденсаторов U
= U1
+ U2
+ U3.
ри
последовательном соединении заряд на
обкладках всех конденсаторов одинаков
Q1
= Q2
= Q3,
а напряжение батареи равняется сумме
напряжений отдельных конденсаторов U
= U1
+ U2
+ U3.
Емкость всей системы последовательно соединенных конденсаторов рассчитывается из соотношения:
1/C = U/Q = 1/C1 + 1/C2 + 1/C3.
Емкость батареи последовательно соединенных конденсаторов всегда меньше, чем емкость каждого из этих конденсаторов в отдельности.
9. Пусть конденсатор ёмкостью C заряжен до напряжения U0. Энергия, запасённая в конденсаторе составляет
![]()

![]()
Параллельный колебательный контур
При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток I, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора EC = 0. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
![]() ,
где L —
индуктивность
катушки, I0 —
максимальное значение тока.
,
где L —
индуктивность
катушки, I0 —
максимальное значение тока.
10.
|
где R = const.
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
|
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
11. Электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь площадь поперечного сечения проводника:
R = р l / S,
где - R - сопротивление проводника, ом, l - длина в проводника в м, S - площадь поперечного сечения проводника, мм2.
12. При последовательном соединении проводников сила тока во всех проводниках одинакова:
I1 = I2 = I. |
По закону Ома, напряжения U1 и U2 на проводниках равны
U1 = IR1, U2 = IR2. |
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
U = U1 + U2 = I(R1 + R2) = IR, |
где R – электрическое сопротивление всей цепи. Отсюда следует:
|
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
При параллельном соединении напряжения U1 и U2 на обоих проводниках одинаковы:
U1 = U2 = U. |
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
I = I1 + I2. |
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно, I = I1 + I2.
Параллельное соединение проводников. |
Записывая на основании закона Ома
|
где R – электрическое сопротивление всей цепи, получим
|
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
13. Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):
 .
.
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.
Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:
для
постоянных напряжений
![]() ;
;
для
переменных напряжений
![]() .
.
Иными
словами, при обходе цепи по контуру,
потенциал, изменяясь, возвращается к
исходному значению. Если цепь содержит
![]() ветвей,
из которых содержат источники тока
ветви в количестве
ветвей,
из которых содержат источники тока
ветви в количестве
![]() ,
то она описывается
,
то она описывается
![]() уравнениями
напряжений. Частным случаем второго
правила для цепи, состоящей из одного
контура, является закон Ома для этой
цепи.
уравнениями
напряжений. Частным случаем второго
правила для цепи, состоящей из одного
контура, является закон Ома для этой
цепи.
14. Напряжённость магнитного поля в центре кругового тока Н = m0I/2R (R — радиус витка с током I)
15.
17. Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Силой Лоренца называют иногда силу, действующую на движущуюся частицу лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1] иначе говоря, со стороны электрического и магнитного полей:
![]() (в
СИ)
(в
СИ)
