
- •Требования к оформлению решений задач
- •Задачи к индивидуальному домашнему заданию №1
- •Прямлинейное и криволинейное поступательное движение тела
- •Вращательное движение тела
- •Импульс тела, второй закон ньютона
- •Столкновения тел. Теорема о кинетической энергии тела. Закон сохранения механической энергии.
- •Дополнительные задачи
- •Задачи, которые годятся лишь для контрольных вопросов или должны быть перенесены в другой раздел
- •Задачи к индивидуальному домашнему заданию №3
- •Моменты инерции тел
- •Движение круглых тел по наклонной плоскости
- •2)Движение круглых тел по наклонной плоскости
- •Задачи к индивидуальному домашнему заданию №4
- •Вращательное движение
- •Законы сохранения энергии и момента импульса
- •Задачи к индивидуальному домашнему заданию №5
- •Колебания физического маятника
- •Затухающие колебания
- •Дополнительные задачи
- •Колебания
Дополнительные задачи
-
1) Тело массой
 ,
подвешенное на нити длиной
,
подвешенное на нити длиной
 к потолку движущегося вверх с ускорением
к потолку движущегося вверх с ускорением
 лифте совершает вращательное движение
в горизонтальной плоскости с частотой
лифте совершает вращательное движение
в горизонтальной плоскости с частотой
 .
При этом угол отклонения нити от
вертикали составляет
.
При этом угол отклонения нити от
вертикали составляет
 .
Найдите ускорение
.
Найдите ускорение
 подъема лифта. Чему равно натяжение
нити?
подъема лифта. Чему равно натяжение
нити?
2)
-
1) Мотоциклист движется по внутренней поверхности вертикального цилиндра (цирковой аттракцион) радиусом 25 м. Коэффициент трения шин мотоцикла о поверхность цилиндра равен 0.25. Какой должна быть минимальная скорость мотоциклиста, чтобы мотоциклист не упал вниз?
2)
-
1) Тело скатывается с некоторой высоты наклонной плоскости с углом наклона
 и ударяется в ее основании абсолютно
упруго о массивную стенку, перпендикулярную
наклонной плоскости, и после удара
поднимается на высоту в два раза меньшую
исходной. Найти коэффициент трения
тела о плоскость.
и ударяется в ее основании абсолютно
упруго о массивную стенку, перпендикулярную
наклонной плоскости, и после удара
поднимается на высоту в два раза меньшую
исходной. Найти коэффициент трения
тела о плоскость.
2)
-
1) Пружина длиной
 и жесткостью
и жесткостью
 надета на невесомый стержень. К концу
пружины прикреплено тело массой
надета на невесомый стержень. К концу
пружины прикреплено тело массой
 ,
которое может перемещаться вдоль
стержня без трения. Стержень, прикрепленный
другим концом к горизонтальной оси
вращения, отклоняют на угол
,
которое может перемещаться вдоль
стержня без трения. Стержень, прикрепленный
другим концом к горизонтальной оси
вращения, отклоняют на угол
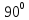 и отпускают. Найти удлинение пружины
при прохождении телом положения
равновесия.
и отпускают. Найти удлинение пружины
при прохождении телом положения
равновесия.
2)
Задачи, которые годятся лишь для контрольных вопросов или должны быть перенесены в другой раздел
-
Найти работу, которую нужно совершить, чтобы увеличить скорость движения тела от
 до
до
 на пути
на пути
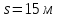 .
На всем пути действует постоянная сила
трения
.
На всем пути действует постоянная сила
трения
 .
Масса тела
.
Масса тела
 .
. -
Две пружины жесткостью 3102 Н/м и 6102 Н/м соединены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина растянута на 3 см. Определить также коэффициент жесткости системы двух пружин.
Задачи к индивидуальному домашнему заданию №3
-
Моменты инерции тел
-
Движение круглых тел по наклонной плоскости
-
1) Вывести формулу для момента инерции равностороннего треугольника массой
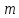 и сторонами длиной
и сторонами длиной
 относительно оси вращения, проходящей
через его вершину, перпендикулярно
плоскости треугольника.
относительно оси вращения, проходящей
через его вершину, перпендикулярно
плоскости треугольника. -
1) Вывести формулу для момента инерции каркаса равностороннего треугольника массой
 и сторонами длиной
и сторонами длиной
 относительно оси вращения, проходящей
через его вершину, перпендикулярно
плоскости треугольника.
относительно оси вращения, проходящей
через его вершину, перпендикулярно
плоскости треугольника. -
1) Вывести формулу для момента инерции равнобедренного треугольника массой
 ,
с длиной боковых сторон, равной
,
с длиной боковых сторон, равной
 ,
и углом при вершине, равном
,
и углом при вершине, равном
 ,
относительно оси вращения, проходящей
вдоль высоты треугольника.
,
относительно оси вращения, проходящей
вдоль высоты треугольника. -
1) Вывести формулу для момента инерции равностороннего треугольника массой
 и сторонами длиной
и сторонами длиной
 относительно оси вращения, проходящей
вдоль одной из его сторон.
относительно оси вращения, проходящей
вдоль одной из его сторон. -
1) Вывести формулу для момента инерции равностороннего треугольника массой
 и сторонами длиной
и сторонами длиной
 относительно оси вращения, совпадающей
с прямой, проходящей через середины
двух сторон треугольника параллельно
его третьей стороне.
относительно оси вращения, совпадающей
с прямой, проходящей через середины
двух сторон треугольника параллельно
его третьей стороне. -
1) Вывести формулу для момента инерции равностороннего треугольника массой
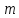 и сторонами длиной
и сторонами длиной
 относительно оси вращения, лежащей
в плоскости треугольника и проходящей
через его вершину параллельно
противоположной стороне.
относительно оси вращения, лежащей
в плоскости треугольника и проходящей
через его вершину параллельно
противоположной стороне.
-
1) Вывести формулу для момента инерции каркаса равнобедренного треугольника массой
 ,
с длиной боковых сторон, равной
,
с длиной боковых сторон, равной
 ,
и углом при вершине, равном
,
и углом при вершине, равном
 ,
относительно оси вращения, проходящей
через его вершину, перпендикулярно
плоскости треугольника.
,
относительно оси вращения, проходящей
через его вершину, перпендикулярно
плоскости треугольника.
-
1) Вывести формулу для момента инерции каркаса равнобедренного треугольника массой
 ,
с длиной боковых сторон, равной
,
с длиной боковых сторон, равной ,
и углом при вершине, равном
,
и углом при вершине, равном
 ,
относительно оси вращения, проходящей
вдоль высоты треугольника.
,
относительно оси вращения, проходящей
вдоль высоты треугольника.
-
1) Вывести формулу для момента инерции прямоугольника массой
 со сторонами
со сторонами
 и
и
 относительно
оси вращения, проходящей через его ЦМ,
перпендикулярно его плоскости.
относительно
оси вращения, проходящей через его ЦМ,
перпендикулярно его плоскости. -
1) Вывести формулу для момента инерции каркаса прямоугольника массой
 со сторонами
со сторонами
 и
и
 относительно оси вращения, проходящей
через его ЦМ, перпендикулярно его
плоскости.
относительно оси вращения, проходящей
через его ЦМ, перпендикулярно его
плоскости. -
1) Вывести формулу для момента инерции каркаса прямоугольника массой
 со сторонами
со сторонами
 и
и
 относительно оси вращения, проходящей
в плоскости прямоугольника вдоль одной
из его диагоналей.
относительно оси вращения, проходящей
в плоскости прямоугольника вдоль одной
из его диагоналей.
-
1) Вывести формулу для момента инерции каркаса ромба массой
 с длиной сторон, равной
с длиной сторон, равной
 ,
и острым углом при вершине, равном
,
и острым углом при вершине, равном
 ,
относительно оси вращения, проходящей
в плоскости ромба вдоль его большей
диагонали.
,
относительно оси вращения, проходящей
в плоскости ромба вдоль его большей
диагонали. -
1) Вывести формулу для момента инерции диска массой
 и радиусом
и радиусом
 относительно оси вращения, проходящей
через его ЦМ, перпендикулярно плоскости
диска.
относительно оси вращения, проходящей
через его ЦМ, перпендикулярно плоскости
диска. -
1) Вывести формулу для момента инерции диска массой
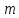 и радиусом
и радиусом
 относительно оси вращения, проходящей
вдоль его диаметра.
относительно оси вращения, проходящей
вдоль его диаметра.
-
1) Вывести формулу для момента инерции кольца массой m и с внутренним и внешним радиусами, равными
 и
и
 относительно оси вращения, проходящей
через его ЦМ, перпендикулярно плоскости
кольца. Формулу привести к виду
относительно оси вращения, проходящей
через его ЦМ, перпендикулярно плоскости
кольца. Формулу привести к виду
 .
. -
1) Вывести формулу для момента инерции кольца массой
 и с внутренним и внешним радиусами,
равными
и с внутренним и внешним радиусами,
равными
 и
и
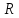 относительно оси вращения, проходящей
вдоль его диаметра.
относительно оси вращения, проходящей
вдоль его диаметра.
-
1) Вывести формулу для момента инерции кругового сектора диска массой
 радиусом
радиусом
 относительно оси вращения, перпендикулярной
его плоскости и проходящей через его
вершину.
относительно оси вращения, перпендикулярной
его плоскости и проходящей через его
вершину. -
1) Вывести формулу для момента инерции кругового сектора массой
 ,
радиусом
,
радиусом
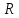 и
углом
и
углом
 при его вершине относительно оси
вращения, лежащей в его плоскости и
проходящей через его ось симметрии.
при его вершине относительно оси
вращения, лежащей в его плоскости и
проходящей через его ось симметрии. -
1) Вывести формулу для момента инерции шара массой
 и радиусом
и радиусом
 относительно оси вращения, проходящей
через его ЦМ.
относительно оси вращения, проходящей
через его ЦМ. -
1) Вывести формулу для момента инерции шарового слоя массой
 с внутренним и внешним радиусами,
равными
с внутренним и внешним радиусами,
равными
 и
и
 относительно оси вращения, проходящей
через его ЦМ. Рассмотреть момент инерции
сферы массой
относительно оси вращения, проходящей
через его ЦМ. Рассмотреть момент инерции
сферы массой
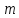 и радиусом
и радиусом
 как частный случай. Для предельного
перехода воспользоваться правилом
Лопиталя.
как частный случай. Для предельного
перехода воспользоваться правилом
Лопиталя. -
1) Вывести формулу для момента инерции прямого сплошного конуса массой
 с радиусом основания
с радиусом основания
 и высотой
и высотой
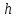 относительно
оси вращения, проходящей через его ось
симметрии.
относительно
оси вращения, проходящей через его ось
симметрии. -
1) Вывести формулу для момента инерции прямого пустотелого конуса массой
 с радиусом основания
с радиусом основания
 и высотой
и высотой
 относительно оси вращения, проходящей
через его ось симметрии.
относительно оси вращения, проходящей
через его ось симметрии. -
1) В однородном диске радиусом
 вырезано круговое отверстие диаметром,
равным
вырезано круговое отверстие диаметром,
равным
 .
Центр отверстия удален от оси диска на
расстояние
.
Центр отверстия удален от оси диска на
расстояние
 .
Масса диска с отверстием равна
.
Масса диска с отверстием равна
 .
Определить момент
инерции тела относительно оси, проходящей
через центр диска, перпендикулярно его
плоскости.
.
Определить момент
инерции тела относительно оси, проходящей
через центр диска, перпендикулярно его
плоскости.
-
1) Вывести формулу для расчета момента инерции однородной тонкой прямоугольной пластинки массы m, длины a и ширины b относительно оси, перпендикулярной к пластинке и проходящей через одну из ее вершин.
-
1)
 шариков
насажены на длинный невесомый стержень.
Первый шарик имеет массу
шариков
насажены на длинный невесомый стержень.
Первый шарик имеет массу
 ,
второй –
,
второй –
 ,
,
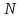 -ый
–
-ый
–
 .
Первый шарик находится на расстоянии
.
Первый шарик находится на расстоянии
 от конца стержня. Расстояние между
шариками также равно
от конца стержня. Расстояние между
шариками также равно
 .
Выведите формулы для момента инерции
и положения ЦМ этой системы
.
Выведите формулы для момента инерции
и положения ЦМ этой системы
 шариков относительно конца стержня.
шариков относительно конца стержня. -
1) Вывести формулу для момента инерции кольца массой
 и с внутренним и внешним радиусами,
равными
и с внутренним и внешним радиусами,
равными
 и
и
 относительно оси вращения, проходящей
вдоль его диаметра.
относительно оси вращения, проходящей
вдоль его диаметра.
