
- •Требования к оформлению решений задач
- •Задачи к индивидуальному домашнему заданию №1
- •Прямлинейное и криволинейное поступательное движение тела
- •Вращательное движение тела
- •Импульс тела, второй закон ньютона
- •Столкновения тел. Теорема о кинетической энергии тела. Закон сохранения механической энергии.
- •Дополнительные задачи
- •Задачи, которые годятся лишь для контрольных вопросов или должны быть перенесены в другой раздел
- •Задачи к индивидуальному домашнему заданию №3
- •Моменты инерции тел
- •Движение круглых тел по наклонной плоскости
- •2)Движение круглых тел по наклонной плоскости
- •Задачи к индивидуальному домашнему заданию №4
- •Вращательное движение
- •Законы сохранения энергии и момента импульса
- •Задачи к индивидуальному домашнему заданию №5
- •Колебания физического маятника
- •Затухающие колебания
- •Дополнительные задачи
- •Колебания
Требования к оформлению решений задач
-
Решения задач оформляются в формате А 4. Оформление решений в тетрадном формате, на клочках бумаги, на бумаге с бахромой запрещено.
-
Задача должна содержать таблицу Дано (СИ) – Найти и рисунок, поясняющий систему обозначений, принятых в задаче, геометрических параметров (длин: l, L, s, S, r,R и т.д., углов:
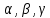 и т.д.) и векторов: r,
v,
a,
F,
N,
mg
(на письме
и т.д.) и векторов: r,
v,
a,
F,
N,
mg
(на письме
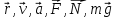 )
и т.д. Появление числовых значений
параметров на рисунке недопустимо.
Например, числовое значение угла
)
и т.д. Появление числовых значений
параметров на рисунке недопустимо.
Например, числовое значение угла
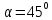 должно помещаться в таблице Дано, а не
на рисунке.
должно помещаться в таблице Дано, а не
на рисунке.
-
Поиск решения задачи (рассуждения от противного) не являются решением, а черновыми рассуждениями. Черновики не проверяются.
-
Решение должно быть построено в виде последовательного алгоритма без неоправданной подстановки формул в формулу. Так, как если бы решение задачи программировалось для решения на компьютере.
-
Неправильное логическое расположение формул не является решением и не проверяемо.
-
Расчеты по формуле должны проводиться сразу же после формулы, а полученные числовые значения параметров могут подставляться в другие последующие формулы. Это удобней, чем подстановка формулы в формулу. Решения задач и логика построения их решения в этом случае быстрее проверяются.
-
Результаты вычислений оформляются в виде Ответа к задаче. После буквенного обозначения параметра должно стоять число с указанием его размерности. Ответ:
 ,
,
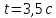 ,
,
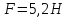 и т.д.
и т.д.
Задачи к индивидуальному домашнему заданию №1
-
Прямлинейное и криволинейное поступательное движение тела
-
Вращательное движение тела
-
1) Радиус-вектор, определяющий положение движущейся частицы меняется по закону
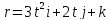 ,
где
,
где
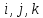 орты осей
орты осей
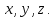 Найти модуль скорости
Найти модуль скорости
 и ускорения
и ускорения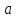 в момент времени
в момент времени
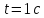 ,
а также перемещение
,
а также перемещение
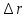 тела за этот промежуток времени. Чему
равно касательное
тела за этот промежуток времени. Чему
равно касательное
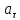 и нормальное
и нормальное
 ускорение тела в этот момент и радиус
ускорение тела в этот момент и радиус
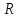 кривизны траектории в точке, в которой
оказалось тело?
кривизны траектории в точке, в которой
оказалось тело?
2) Колесо вращается
так, что его угловая координата задана
уравнением
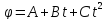 , где
, где
 .
Найдите угловую скорость
.
Найдите угловую скорость
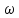 и угловое ускорение
и угловое ускорение
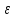 и угол
и угол
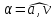 между направлением вектора полного
ускорения и вектора скорости точек на
ободе колеса через
между направлением вектора полного
ускорения и вектора скорости точек на
ободе колеса через
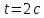 после начала движения. Сколько оборотов
после начала движения. Сколько оборотов
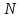 сделало тело и чему равно среднее
значение углового ускорения
сделало тело и чему равно среднее
значение углового ускорения
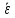 и угловой скорости
и угловой скорости
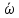 за это время?
за это время?
-
1) Материальная точка движется в плоскости так, что зависимость координат от времени дается уравнениями
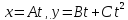 ,
где
,
где
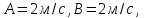 C
= 1 м/с2. Определите скорость
C
= 1 м/с2. Определите скорость
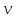 ,
ускорение
,
ускорение
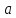 и перемещение
и перемещение
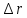 частицы через
частицы через
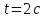 после начала движения. Чему равно
касательное
после начала движения. Чему равно
касательное
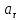 и нормальное
и нормальное
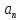 ускорение тела в этот момент и радиус
ускорение тела в этот момент и радиус
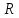 кривизны траектории в точке, в которой
оказалось тело?
кривизны траектории в точке, в которой
оказалось тело?
2) Диск вращается
вокруг неподвижной оси так, что закон
изменения угла поворота его радиуса
определяется уравнением
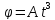 (рад),
(рад),
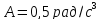 . Найдите нормальное
. Найдите нормальное
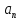 ,
касательное
,
касательное
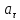 и полное
и полное
 ускорение его точек, отстоящих от оси
вращения на
ускорение его точек, отстоящих от оси
вращения на
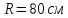 через
через
 после начала вращения. Каков угол
после начала вращения. Каков угол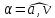 между направлением вектора полного
ускорения и вектора скорости точек
диска в этот момент времени? Сколько
оборотов
между направлением вектора полного
ускорения и вектора скорости точек
диска в этот момент времени? Сколько
оборотов
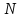 сделает диск?
сделает диск?
-
1) Материальная точка движется согласно уравнению
 ,
где
,
где
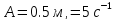 .
Изобразите на рисунке траекторию и
направление движения точки. Определите
модуль ее скорости
.
Изобразите на рисунке траекторию и
направление движения точки. Определите
модуль ее скорости
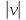 и модуль полного
и модуль полного
 и нормального ускорения
и нормального ускорения
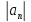 .
.
2) Диск радиусом вращается вокруг неподвижной оси так,
что закон изменения угла поворота его
радиуса определяется уравнением
вращается вокруг неподвижной оси так,
что закон изменения угла поворота его
радиуса определяется уравнением
 ,
где
,
где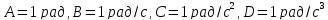 .
Вычислите нормальное
.
Вычислите нормальное
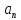 ,
касательное
,
касательное
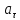 и полное
и полное
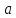 ускорение точек на ободе диска к концу
первой секунды. Каков угол
ускорение точек на ободе диска к концу
первой секунды. Каков угол
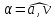 между направлением вектора полного
ускорения и вектора скорости этих точек
в этот момент времени? Сколько оборотов
между направлением вектора полного
ускорения и вектора скорости этих точек
в этот момент времени? Сколько оборотов сделает диск и чему равно среднее
значение его углового ускорения
сделает диск и чему равно среднее
значение его углового ускорения
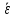 и угловой скорости
и угловой скорости
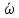 за это время?
за это время?
-
1) Координата
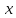 движущейся
частицы меняется по закону
движущейся
частицы меняется по закону
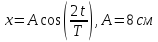 ,
,
 .
Найти выражения для проекций на ось
.
Найти выражения для проекций на ось
 скорости
скорости
 и ускорения
и ускорения
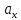 частицы, среднюю скорость
частицы, среднюю скорость
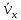 и среднее ускорение
и среднее ускорение
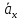 частицы на интервале времени от
частицы на интервале времени от
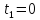 до
до
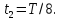 Чему равно перемещение
Чему равно перемещение
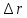 и путь
и путь
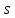 ,
пройденный точкой, за этот промежуток
времени?
,
пройденный точкой, за этот промежуток
времени?
2) Частица движется
по окружности так, что ее угловая
координата задана уравнением
 , где
, где
 .
Вычислите радиус окружности, если к
концу первой секунды движения нормальное
ускорение частицы на ней равно
.
Вычислите радиус окружности, если к
концу первой секунды движения нормальное
ускорение частицы на ней равно
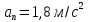 .
Чему равно полное ускорение
.
Чему равно полное ускорение
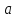 и угол
и угол
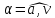 между направлением вектора полного
ускорения и вектора скорости частицы
за это время? Сколько оборотов
между направлением вектора полного
ускорения и вектора скорости частицы
за это время? Сколько оборотов
 сделает частица и чему равно среднее
значение ее углового ускорения
сделает частица и чему равно среднее
значение ее углового ускорения
 и угловой скорости
и угловой скорости
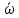 за это время?
за это время?
-
1) Материальная точка движется в плоскости
 по закону
по закону
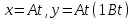 ,
где
,
где
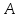 и
и
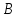 положительные константы. Найдите
уравнение кривой
положительные константы. Найдите
уравнение кривой
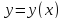 ,
описывающей траекторию частицы, и
изобразите ее график. Определите
зависимости от времени величин скорости
,
описывающей траекторию частицы, и
изобразите ее график. Определите
зависимости от времени величин скорости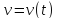 и ускорения
и ускорения
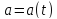 частицы и постройте их графики.
частицы и постройте их графики.
2) Диск вращается
вокруг неподвижной оси так, что угол
поворота его радиуса определяется
уравнением
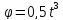 (рад). Вычислите полное ускорение
(рад). Вычислите полное ускорение
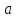 точек, отстоящих от оси вращения на
точек, отстоящих от оси вращения на
 к концу второй секунды движения. Каков
угол
к концу второй секунды движения. Каков
угол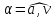 между направлением вектора полного
ускорения и вектора скорости этих точек
в этот момент времени? Сколько оборотов
между направлением вектора полного
ускорения и вектора скорости этих точек
в этот момент времени? Сколько оборотов
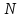 сделает диск и чему равно среднее
значение его углового ускорения
сделает диск и чему равно среднее
значение его углового ускорения
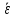 и угловой скорости
и угловой скорости
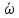 за это время?
за это время?
-
1) Закон движения двух материальных точек выражается уравнениями
 ;
;
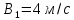 ,
,
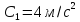 ,
,
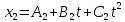 ;
;
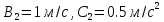 .
Определите момент времени
.
Определите момент времени
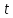 ,
когда скорости точек будут одинаковы:
,
когда скорости точек будут одинаковы:
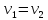 .
Найдите значения скорости
.
Найдите значения скорости
 и ускорений
и ускорений
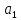 и
и
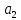 точек в этот момент. Покажите их
направления для каждого из тел на
рисунке. Чему равны средние скорости
точек в этот момент. Покажите их
направления для каждого из тел на
рисунке. Чему равны средние скорости
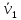 и
и
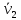 тел за интервал времени до момента их
встречи?
тел за интервал времени до момента их
встречи?
2) Колесо радиусом
R = 3 см вращается так, что зависимость
угла поворота радиуса колеса от времени
дается уравнением
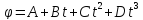 ,
где
,
где
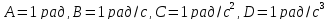 .
Чему равны средняя угловая скорость
.
Чему равны средняя угловая скорость
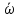 и среднее угловое ускорение точек на
ободе колеса за
и среднее угловое ускорение точек на
ободе колеса за
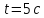 его вращения. Вычислите касательное
его вращения. Вычислите касательное
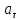 ,
нормальное
,
нормальное
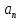 и полное
и полное
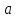 ускорение точек на ободе колеса и
определите угол
ускорение точек на ободе колеса и
определите угол
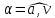 между направлением вектора полного
ускорения и вектора скорости точек на
ободе в конечный момент времени? Сколько
оборотов
между направлением вектора полного
ускорения и вектора скорости точек на
ободе в конечный момент времени? Сколько
оборотов
 сделает колесо за это время?
сделает колесо за это время?
-
1) В момент времени
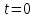 частица начала двигаться из начала
координат в положительном направлении
оси
частица начала двигаться из начала
координат в положительном направлении
оси
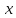 .
Ее скорость меняется по закону
.
Ее скорость меняется по закону
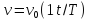 ,
где
,
где
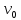 - вектор начальной скорости, модуль
которого
- вектор начальной скорости, модуль
которого
 .
Найдите координату
.
Найдите координату
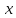 скорость
скорость
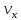 и ускорение
и ускорение
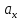 частицы в момент времени
частицы в момент времени
 и постройте графики зависимости пути
и постройте графики зависимости пути
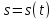 ,
скорости
,
скорости
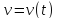 и ускорения
и ускорения
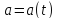 частицы от времени
частицы от времени
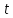 .
Чему равны средняя скорость
.
Чему равны средняя скорость
 и среднее ускорение
и среднее ускорение
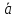 частицы за этот промежуток времени?
Как их определить графически?
частицы за этот промежуток времени?
Как их определить графически?
2) Колесо вращается
с постоянным угловым ускорением
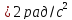 .
Через
.
Через
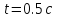 после начала движения полное ускорение
точек на ободе колеса стало равным
после начала движения полное ускорение
точек на ободе колеса стало равным
 .
Найти радиус колеса. Чему равны средняя
угловая скорость
.
Найти радиус колеса. Чему равны средняя
угловая скорость
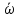 и среднее угловое ускорение
и среднее угловое ускорение
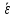 точек на ободе колеса за это время. Каков
угол
точек на ободе колеса за это время. Каков
угол
 между направлением вектора полного
ускорения и вектора скорости точек
колеса в конечный момент времени? Сколько
оборотов
между направлением вектора полного
ускорения и вектора скорости точек
колеса в конечный момент времени? Сколько
оборотов
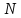 сделает колесо за это время?
сделает колесо за это время?
-
1) Зависимость координаты частицы от времени дается уравнением
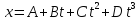 ,
где
,
где
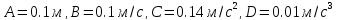 .
Найдите среднее ускорение
.
Найдите среднее ускорение
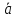 и среднюю скорость
и среднюю скорость
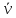 частицы за первые 10 с движения. Как их
определить графически?
частицы за первые 10 с движения. Как их
определить графически?
2) Через t = 10 с
после начала вращения с постоянным
угловым ускорением полное ускорение
точек на ободе диска радиусом R = 5
см равно a = 15 см/с2. Определите
угловое ускорение диска, а также
нормальное и тангенциальное ускорения
точек обода диска в конечный момент
времени. Чему равны средние значения
углового ускорения
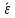 и угловой скорости
и угловой скорости
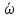 диска и сколько оборотов
диска и сколько оборотов
 он сделает за это время? Каков угол
он сделает за это время? Каков угол
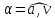 между направлением вектора полного
ускорения и вектора скорости точек на
ободе диска в конечный момент времени?
между направлением вектора полного
ускорения и вектора скорости точек на
ободе диска в конечный момент времени?
-
1) В течение интервала времени
 скорость тела меняется по закону
скорость тела меняется по закону
 , где
, где
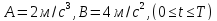 .
Найдите среднюю скорость
.
Найдите среднюю скорость
 ,
и среднее ускорение
,
и среднее ускорение
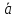 тела за этот промежуток времени. Как
их определить графически?
тела за этот промежуток времени. Как
их определить графически?
2) Колесо вращается
так, что угол поворота его радиуса
определяется уравнением
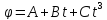 , где
, где
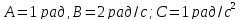 .
Найдите угловую скорость
.
Найдите угловую скорость
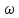 и угловое ускорение
и угловое ускорение
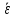 точек на ободе колеса через
точек на ободе колеса через
 после начала движения и угол
после начала движения и угол
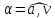 между направлением вектора полного
ускорения и вектора скорости точек
колеса в этот момент времени. Чему равны
средняя угловая скорость
между направлением вектора полного
ускорения и вектора скорости точек
колеса в этот момент времени. Чему равны
средняя угловая скорость
 и среднее угловое ускорение
и среднее угловое ускорение
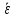 вращения колеса и сколько оборотов
вращения колеса и сколько оборотов
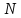 оно сделает за это время?
оно сделает за это время?
-
1) С вышки бросили камень в горизонтальном направлении. Через
 камень упал на землю на расстоянии
камень упал на землю на расстоянии
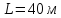 от основания вышки. Определите начальную
от основания вышки. Определите начальную
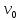 и конечную
и конечную
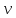 скорости камня. Под каким углом
скорости камня. Под каким углом
 к горизонту упадет камень? Чему
равен радиус
к горизонту упадет камень? Чему
равен радиус
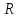 кривизны траектории движения камня в
точке его падения? Чему равны
средние скорости
кривизны траектории движения камня в
точке его падения? Чему равны
средние скорости
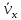 и
и
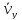 тела в горизонтальном и вертикальном
направлениях его движения за время
полета?
тела в горизонтальном и вертикальном
направлениях его движения за время
полета?
-
Тело, вращающееся по окружности радиуса
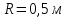 с постоянным угловым ускорением,
увеличило свою частоту вращения от
с постоянным угловым ускорением,
увеличило свою частоту вращения от
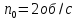 до
до
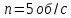 ,
совершив при этом
,
совершив при этом
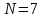 оборотов. Найти угловое ускорение
оборотов. Найти угловое ускорение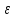 и время
и время
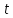 вращения тела, угол
вращения тела, угол
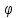 его поворота, начальную
его поворота, начальную
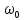 и конечную
и конечную
 угловые скорости. Чему равны путь
угловые скорости. Чему равны путь
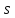 ,
пройденный телом вдоль окружности, его
начальная
,
пройденный телом вдоль окружности, его
начальная
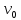 и конечная
и конечная
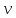 скорости, касательное
скорости, касательное
 ,
центростремительное
,
центростремительное
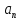 и полное
и полное
 ускорение?
ускорение?
-
1) Материальная точка движется в плоскости
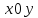 по закону
по закону
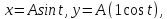 где
где
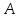 и
и
 положительные константы. Найдите
уравнение кривой, описывающей траекторию
движения точки, изобразите ее вид и
направление движения частицы. С какой
скоростью
положительные константы. Найдите
уравнение кривой, описывающей траекторию
движения точки, изобразите ее вид и
направление движения частицы. С какой
скоростью
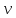 и с каким нормальным ускорением
и с каким нормальным ускорением
 движется точка вдоль траектории? Какой
путь
движется точка вдоль траектории? Какой
путь
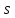 она пройдет за период
она пройдет за период
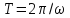 ее движения?
ее движения?
2) Тело, вращающееся
по окружности радиуса
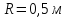 с постоянным угловым ускорением, за
время
с постоянным угловым ускорением, за
время
 увеличило свою частоту вращения от
увеличило свою частоту вращения от
 до
до
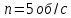 .
Найти число оборотов
.
Найти число оборотов
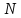 тела за это время и его угловое ускорение
тела за это время и его угловое ускорение
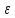 вращения, угол
вращения, угол
 его поворота, начальную
его поворота, начальную
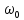 и конечную
и конечную
 угловые скорости. Чему равны путь
угловые скорости. Чему равны путь
 ,
пройденный телом вдоль окружности, его
начальная
,
пройденный телом вдоль окружности, его
начальная
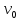 и конечная
и конечная
 скорости, касательное
скорости, касательное
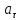 ,
центростремительное
,
центростремительное
 и полное
и полное
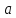 ускорение в конечный момент времени?
ускорение в конечный момент времени?
-
1) Камень брошен с поверхности земли со скоростью
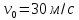 под углом
под углом
 к горизонту. Определите радиусы кривизны
к горизонту. Определите радиусы кривизны
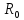 и
и
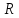 траектории в нижней точке броска и в
ее верхней точке. Чему равно время
траектории в нижней точке броска и в
ее верхней точке. Чему равно время
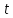 полета камня до его падения на землю?
Во сколько раз отличаются дальность
полета
полета камня до его падения на землю?
Во сколько раз отличаются дальность
полета
 и максимальная высота
и максимальная высота
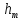 подъема камня?
подъема камня?
2) Частица движется
по окружности так, что ее угловая
координата задана уравнением
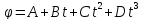 ,
где
,
где
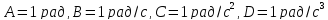 .
Вычислите радиус
.
Вычислите радиус
 окружности, если через время
окружности, если через время
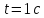 движения ее касательное ускорение равно
движения ее касательное ускорение равно
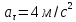 .
Чему равно среднее угловое ускорение
.
Чему равно среднее угловое ускорение
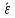 и средняя угловая скорость
и средняя угловая скорость
 частицы за это время, а также полное
ускорение
частицы за это время, а также полное
ускорение
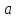 частицы и угол
частицы и угол
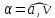 между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени? Сколько
оборотов
между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени? Сколько
оборотов
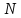 сделает частица за это время?
сделает частица за это время?
-
1) Компоненты скорости частицы меняются по закону
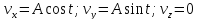 ,
где
,
где
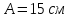 и
и
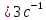 .
Изобразите на рисунке траекторию
частицы и направление ее движения. Чему
равны скорость
.
Изобразите на рисунке траекторию
частицы и направление ее движения. Чему
равны скорость
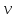 и нормальное ускорение
и нормальное ускорение
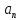 движения частицы? Какой путь
движения частицы? Какой путь
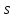 пройдет частица за период
пройдет частица за период
 ее движения?
ее движения?
-
Частица движется по окружности так, что ее угловая координата задана уравнением
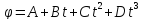 ,
где
,
где
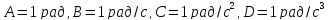 .
Вычислите радиус
.
Вычислите радиус
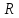 окружности, если через время
окружности, если через время
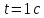 движения ее касательное ускорение
равно
движения ее касательное ускорение
равно
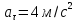 .
Чему равно среднее угловое ускорение
.
Чему равно среднее угловое ускорение
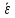 и средняя угловая скорость
и средняя угловая скорость
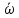 частицы за это время, а также полное
ускорение
частицы за это время, а также полное
ускорение
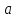 частицы и угол
частицы и угол
 между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени? Сколько
оборотов
между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени? Сколько
оборотов
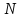 сделает частица за это время?
сделает частица за это время?
-
1) Частица движется по окружности радиусом 2 см, при этом зависимость ее пути от времени задана уравнением
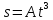 (см),
(см),
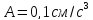 . Найдите нормальное
. Найдите нормальное
 ,
касательное
,
касательное
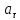 и полное ускорение частицы в тот момент
времени, когда ее линейная скорость
стала
и полное ускорение частицы в тот момент
времени, когда ее линейная скорость
стала
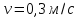 .
Какой путь
.
Какой путь
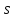 пройдет частица за это время? Каков
угол
пройдет частица за это время? Каков
угол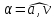 между векторами скорости и полного
ускорения частицы в этот момент времени?
между векторами скорости и полного
ускорения частицы в этот момент времени?
2) Колесо вращается
с постоянным угловым ускорением
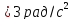 .
Определите число N оборотов, которое
сделает колесо при изменении частоты
вращения от
.
Определите число N оборотов, которое
сделает колесо при изменении частоты
вращения от
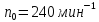 до
до
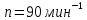 ,
а также время
,
а также время
 ,
в течение которого это произойдет. Через
какое время
,
в течение которого это произойдет. Через
какое время
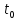 колесо остановится и сколько оборотов
колесо остановится и сколько оборотов
 сделает до остановки? Чему равен угол
сделает до остановки? Чему равен угол
 между направлением вектора полного
ускорения и вектора скорости точек на
ободе колеса в начале вращения?
между направлением вектора полного
ускорения и вектора скорости точек на
ободе колеса в начале вращения?
-
1) Нормальное ускорение частицы, движущейся по окружности радиусом
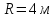 ,
задается уравнением
,
задается уравнением
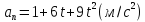 ,
,
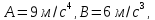
 .
Вычислите касательное
.
Вычислите касательное
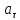 и полное ускорение
и полное ускорение
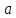 частицы через
частицы через
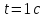 после начала движения. Каков угол
после начала движения. Каков угол
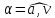 между векторами скорости и полного
ускорения частицы в этот момент времени?
между векторами скорости и полного
ускорения частицы в этот момент времени?
2) Колесо радиуса
R = 1 м вращается так, что зависимость
угла поворота радиуса колеса от времени
дается уравнением
= A + Bt + Ct3, где
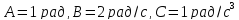 .
Найти линейную скорость
.
Найти линейную скорость
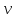 и полное ускорение
и полное ускорение
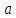 для точек обода через t = 3 с после
начала движения. Чему равны среднее
угловое ускорение
для точек обода через t = 3 с после
начала движения. Чему равны среднее
угловое ускорение
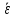 и средняя угловая скорость
и средняя угловая скорость
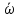 частицы за это время, а также полное
ускорение
частицы за это время, а также полное
ускорение
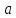 частицы и угол
частицы и угол
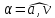 между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени? Сколько
оборотов
между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени? Сколько
оборотов
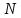 сделает частица за это время?
сделает частица за это время?
-
1) Колесо радиусом
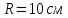 вращается так, что линейная скорость
точек на его ободе задана уравнением
вращается так, что линейная скорость
точек на его ободе задана уравнением
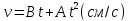 ,
,
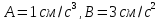 .
Какой путь
.
Какой путь
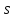 пройдет точка обода колеса за
пройдет точка обода колеса за
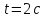 от начала вращения? Найдите касательное
от начала вращения? Найдите касательное
 ,
нормальное
,
нормальное
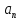 и полное ускорение
и полное ускорение
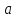 точки и угол
точки и угол
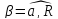 между вектором полного ускорения и
радиусом колеса в этот момент времени.
между вектором полного ускорения и
радиусом колеса в этот момент времени.
2) На барабан радиуса
 намотана нить, барабан вращается вокруг
горизонтальной оси, проходящей через
его ось симметрии, под действием груза,
подвешенного к нити. Груз движется с
постоянным ускорением
намотана нить, барабан вращается вокруг
горизонтальной оси, проходящей через
его ось симметрии, под действием груза,
подвешенного к нити. Груз движется с
постоянным ускорением
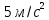 .
Найти угловое ускорение
.
Найти угловое ускорение
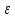 вращения барабана, угловую
вращения барабана, угловую
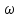 ,
а также линейную скорость
,
а также линейную скорость
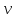 и полное ускорение
и полное ускорение
 точек на его поверхности через
точек на его поверхности через
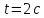 после начала его вращения. На какую
высоту
после начала его вращения. На какую
высоту
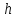 опустится груз и сколько оборотов
опустится груз и сколько оборотов
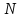 сделает барабан за это время?
сделает барабан за это время?
-
1) Частица движется по окружности, причем зависимость ее дуговой координаты от времени задана уравнением
 ,где
,где
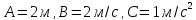 .
В момент времени
.
В момент времени
 ее нормальное ускорение равно
ее нормальное ускорение равно
 .
Найдите полное ускорение
.
Найдите полное ускорение
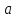 частицы через
частицы через
 после начала движения и угол
после начала движения и угол
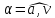 ,
который вектор полного ускорения
составляет с направлением вектора
скорости. Чему равен путь
,
который вектор полного ускорения
составляет с направлением вектора
скорости. Чему равен путь
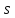 ,
перемещение
,
перемещение
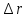 частицы за это время и радиус
частицы за это время и радиус
 окружности, по которой она вращается?
окружности, по которой она вращается?
2) Материальная
точка движется по окружности радиуса
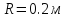 с постоянным угловым ускорением. Через
с постоянным угловым ускорением. Через
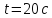 после начала движения угловая скорость
частицы
после начала движения угловая скорость
частицы
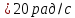 .
Определите число
.
Определите число
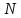 оборотов, которое совершила за это время
частица, а также ее касательное
оборотов, которое совершила за это время
частица, а также ее касательное
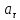 ,
нормальное
,
нормальное
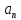 и полное ускорение
и полное ускорение
 точки и угол
точки и угол
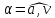 между направлением вектора полного
ускорения и вектора скорости точки в
конечный момент времени. Чему равны
среднее угловое ускорение
между направлением вектора полного
ускорения и вектора скорости точки в
конечный момент времени. Чему равны
среднее угловое ускорение
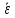 и средняя угловая скорость
и средняя угловая скорость
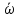 вращения точки за это время?
вращения точки за это время?
-
1) По дуге окружности радиусом
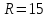 м движется материальная точка. В
некоторый момент времени нормальное
ускорение частицы
м движется материальная точка. В
некоторый момент времени нормальное
ускорение частицы
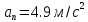 ,
а вектор полного ускорения образует с
радиусом вращения угол
,
а вектор полного ускорения образует с
радиусом вращения угол
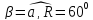 .
Найдите скорость
.
Найдите скорость
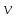 ,
тангенциальное
,
тангенциальное
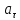 и полное ускорение
и полное ускорение
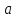 частицы в этот момент времени.
частицы в этот момент времени.
2) Частица движется
по окружности радиуса
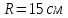 с постоянным тангенциальным ускорением
с постоянным тангенциальным ускорением
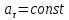 .
Найдите это ускорение, если известно,
что к концу пятого оборота
.
Найдите это ускорение, если известно,
что к концу пятого оборота
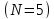 после начала движения скорость частицы
стала равной
после начала движения скорость частицы
стала равной
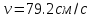 .
Чему равно полное ускорение
.
Чему равно полное ускорение
 частицы и угол
частицы и угол
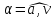 между направлением вектора полного
ускорения и вектора скорости частицы
в этот момент времени?
между направлением вектора полного
ускорения и вектора скорости частицы
в этот момент времени?
-
1) Материальная точка движется по окружности радиуса
 так, что зависимость дуговой координаты
от времени дается уравнением
так, что зависимость дуговой координаты
от времени дается уравнением
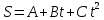 ,
где
,
где
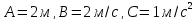 .
Найдите линейную скорость
.
Найдите линейную скорость
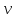 частицы, ее касательное
частицы, ее касательное
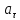 ,
нормальное
,
нормальное
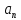 и полное ускорение
и полное ускорение
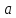 через
через
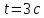 после начала движения. Какой угол
после начала движения. Какой угол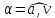 вектор полного ускорения составляет
с вектором скорости в этот момент
времени? Каков путь
вектор полного ускорения составляет
с вектором скорости в этот момент
времени? Каков путь
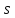 и перемещение
и перемещение
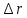 точки за это время?
точки за это время?
2) Колесо вращается
так, что зависимость угла поворота
радиуса колеса от времени дается
уравнением
 ,
где
,
где
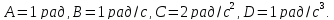 Найти радиус
Найти радиус
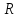 колеса, если известно, что к концу второй
секунды движения нормальное ускорение
точек, лежащих на ободе колеса,
колеса, если известно, что к концу второй
секунды движения нормальное ускорение
точек, лежащих на ободе колеса,
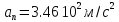 .
Чему равно касательное
.
Чему равно касательное
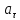 и полное ускорение
и полное ускорение
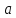 и угол
и угол
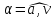 между направлением вектора полного
ускорения и вектора скорости точек
колеса в это время? Чему равны среднее
угловое ускорение
между направлением вектора полного
ускорения и вектора скорости точек
колеса в это время? Чему равны среднее
угловое ускорение
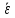 и средняя угловая скорость
и средняя угловая скорость
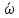 вращения колеса и сколько оборотов
вращения колеса и сколько оборотов
 оно сделает за это время?
оно сделает за это время?
-
1) Движение частицы по кривой задано уравнениями
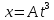 и
и
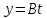 где
где
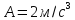 ,
,
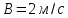 .
Напишите уравнение кривой, по которой
движется частица и постройте ее график
.
Напишите уравнение кривой, по которой
движется частица и постройте ее график
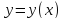 .
Определите скорость
.
Определите скорость
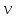 и полное ускорение
и полное ускорение
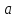 частицы через
частицы через
 после начала движения. Какой угол
после начала движения. Какой угол
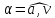 вектор полного ускорения составляет
с вектором скорости в этот момент
времени? Каков радиус
вектор полного ускорения составляет
с вектором скорости в этот момент
времени? Каков радиус
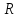 кривизны траектории в точке, в которой
оказалась частица?
кривизны траектории в точке, в которой
оказалась частица?
2) Частица, вращающаяся
по окружности радиуса
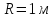 ,
с некоторой начальной частотой вращения
,
с некоторой начальной частотой вращения
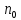 и постоянным угловым ускорением
и постоянным угловым ускорением
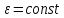 за время
за время
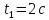 совершила
совершила
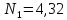 оборота, а за время
оборота, а за время
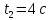
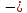
 оборотов. Чему равны касательное
оборотов. Чему равны касательное
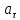 ,
нормальное
,
нормальное
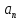 и полное ускорение
и полное ускорение
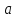 частицы и угол
частицы и угол
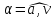 между направлением вектора ее полного
ускорения и вектора скорости в момент
времени
между направлением вектора ее полного
ускорения и вектора скорости в момент
времени
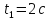 ?
?
-
1) Материальная точка движется в плоскости
 по закону
по закону
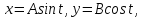 где
где
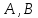 и
и
 положительные константы,
положительные константы,
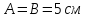 .
Найдите уравнение кривой
.
Найдите уравнение кривой
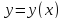 ,
описывающей траекторию частицы,
изобразите ее вид и направление движения
частицы. Чему равны скорость
,
описывающей траекторию частицы,
изобразите ее вид и направление движения
частицы. Чему равны скорость
 и ускорение
и ускорение
 частицы в момент времени
частицы в момент времени
 ?
Какой угол
?
Какой угол
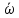 вектор полного ускорения составляет
с вектором скорости в этот момент
времени?
вектор полного ускорения составляет
с вектором скорости в этот момент
времени?
2) Частица вращается
по окружности радиуса
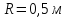 с угловой скоростью, изменяющейся по
закону
с угловой скоростью, изменяющейся по
закону
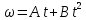 ,
где
,
где
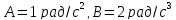 .
Найти среднее угловое ускорение
.
Найти среднее угловое ускорение
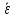 и среднюю угловую скорость
и среднюю угловую скорость
 движения частицы за интервал времени
движения частицы за интервал времени
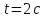 от начала ее движения. Сколько оборотов
от начала ее движения. Сколько оборотов
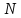 сделает частица за это время? Чему равны
линейная скорость
сделает частица за это время? Чему равны
линейная скорость
 и полное линейное ускорение
и полное линейное ускорение
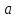 и угол
и угол
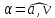 между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени?
между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени?
-
1) Материальная точка движется по дуге окружности радиуса
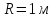 по закону
по закону
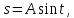 где
где
 смещение из начального положения,
отсчитываемое вдоль дуги,
смещение из начального положения,
отсчитываемое вдоль дуги,
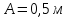 и
и
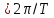 положительные константы. Найдите полное
ускорение
положительные константы. Найдите полное
ускорение
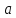 частицы в момент времени
частицы в момент времени
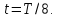 Какой угол
Какой угол
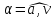 вектор полного ускорения составляет
с вектором скорости в этот момент
времени? Каков пройденный путь
вектор полного ускорения составляет
с вектором скорости в этот момент
времени? Каков пройденный путь
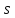 и перемещение
и перемещение
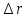 точки за это время (покажите их на
рисунке)?
точки за это время (покажите их на
рисунке)?
2) Частица вращается
по окружности радиуса
 с угловым ускорением, изменяющемся по
закону
с угловым ускорением, изменяющемся по
закону
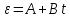 ,
где
,
где
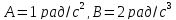 .
Найти среднее угловое ускорение
.
Найти среднее угловое ускорение
 и среднюю угловую скорость
и среднюю угловую скорость
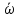 движения частицы за интервал времени
движения частицы за интервал времени
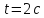 от начала ее движения. Сколько оборотов
от начала ее движения. Сколько оборотов
 сделает частица за это время? Чему равны
линейная скорость
сделает частица за это время? Чему равны
линейная скорость
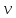 и полное линейное ускорение
и полное линейное ускорение
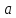 и угол
и угол
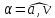 между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени?
между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени?
-
1) Частица движется по окружности радиусом
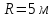 согласно уравнению
согласно уравнению
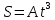 ,
где
,
где
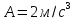 ,
,
 путь, пройденный частицей. В какой
момент времени тангенциальное ускорение
частицы будет равно нормальному?
Вычислите полное ускорение
путь, пройденный частицей. В какой
момент времени тангенциальное ускорение
частицы будет равно нормальному?
Вычислите полное ускорение
 частицы и угол
частицы и угол
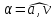 между направлением вектора полного
ускорения и вектора скорости в этот
момент времени.
между направлением вектора полного
ускорения и вектора скорости в этот
момент времени.
2) Колесо вращается
так, что зависимость угла поворота
радиуса колеса от времени дается
уравнением
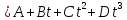 ,
где
,
где
 Найти радиус
Найти радиус
 колеса, если известно, что к концу второй
секунды движения линейная скорость
точек, лежащих на ободе колеса,
колеса, если известно, что к концу второй
секунды движения линейная скорость
точек, лежащих на ободе колеса,
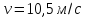 .
Сколько оборотов
.
Сколько оборотов
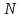 сделает колесо и чему равны среднее
угловое ускорение
сделает колесо и чему равны среднее
угловое ускорение
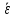 и средняя угловая скорость
и средняя угловая скорость
 его вращения за это время? Чему равны
касательное
его вращения за это время? Чему равны
касательное
 ,
нормальное
,
нормальное
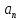 и полное ускорение
и полное ускорение
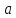 частицы и угол
частицы и угол
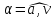 между направлением вектора ее полного
ускорения и вектора скорости в конечный
момент времени?
между направлением вектора ее полного
ускорения и вектора скорости в конечный
момент времени?
-
1) Материальная точка движется по кривой с постоянным тангенциальным ускорением
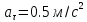 с начальной скоростью
с начальной скоростью
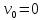 .
Определите полное ускорение
.
Определите полное ускорение
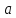 частицы в точке, где радиус кривизны
траектории составляет
частицы в точке, где радиус кривизны
траектории составляет
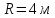 ,
и угол
,
и угол
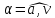 между направлением вектора полного
ускорения и вектора скорости, если
частица движется в этот момент со
скоростью
между направлением вектора полного
ускорения и вектора скорости, если
частица движется в этот момент со
скоростью
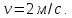
2) Частица вращается
по окружности радиуса
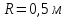 с угловой скоростью, изменяющейся по
закону
с угловой скоростью, изменяющейся по
закону
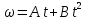 .
Среднее угловое ускорение частицы за
интервал времени
.
Среднее угловое ускорение частицы за
интервал времени
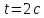 от начала ее движения равно
от начала ее движения равно
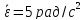 ,
а его мгновенное значение в конечный
момент времени
,
а его мгновенное значение в конечный
момент времени
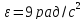 .
Сколько оборотов
.
Сколько оборотов
 сделает частица за это время? Чему равны
линейная скорость
сделает частица за это время? Чему равны
линейная скорость
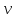 и полное линейное ускорение
и полное линейное ускорение
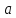 и угол
и угол
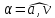 между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени?
между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени?
-
1) Частица движется по окружности радиуса
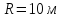 со скоростью
со скоростью
 ,
где
,
где
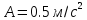 .
Найдите ее полное ускорение в момент
времени, когда она пройдет расстояние
.
Найдите ее полное ускорение в момент
времени, когда она пройдет расстояние
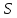 ,
равное 0.1 длины окружности после начала
движения. Каков угол между векторами
полного ускорения и скорости частицы
в этот момент времени?
,
равное 0.1 длины окружности после начала
движения. Каков угол между векторами
полного ускорения и скорости частицы
в этот момент времени?
2) Частица вращается
по окружности радиуса
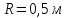 с угловым ускорением, изменяющемся по
закону
с угловым ускорением, изменяющемся по
закону
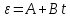 .
Ее мгновенное ускорение в момент времени
.
Ее мгновенное ускорение в момент времени
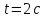 от начала ее движения равно
от начала ее движения равно
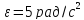 ,
а среднее угловое ускорение за этот
промежуток времени
,
а среднее угловое ускорение за этот
промежуток времени
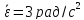 .
Найти среднюю угловую скорость движения
частицы за этот промежуток времени.
Сколько оборотов
.
Найти среднюю угловую скорость движения
частицы за этот промежуток времени.
Сколько оборотов
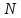 сделает частица за это время? Чему равны
линейная скорость
сделает частица за это время? Чему равны
линейная скорость
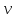 и полное линейное ускорение
и полное линейное ускорение
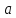 и угол
и угол
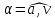 между направлением вектора полного
ускорения и вектора скорости частицы
в этот момент времени?
между направлением вектора полного
ускорения и вектора скорости частицы
в этот момент времени?
-
1) Через t = 10 с после начала вращения с постоянным угловым ускорением полное ускорение точек на ободе диска радиусом R = 5 см равно a = 15 см/с2. Определите угловое ускорение
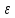 диска, а также нормальное
диска, а также нормальное
 и тангенциальное
и тангенциальное
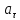 ускорения точек обода через t = 5 с
после начала вращения. Каков угол
ускорения точек обода через t = 5 с
после начала вращения. Каков угол
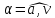 между направлением вектора полного
ускорения и вектора скорости в этот
момент времени?
между направлением вектора полного
ускорения и вектора скорости в этот
момент времени?
2) Частица вращается
по окружности радиуса
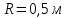 с угловой скоростью, изменяющейся по
закону
с угловой скоростью, изменяющейся по
закону
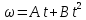 .
Средняя угловая скорость частицы за
интервал времени
.
Средняя угловая скорость частицы за
интервал времени
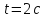 от начала ее движения равна
от начала ее движения равна
 ,
а ее мгновенное значение в конечный
момент времени
,
а ее мгновенное значение в конечный
момент времени
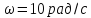 .
Сколько оборотов
.
Сколько оборотов
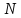 сделает частица за это время? Чему равны
линейная скорость
сделает частица за это время? Чему равны
линейная скорость
 и полное линейное ускорение
и полное линейное ускорение
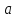 и угол
и угол
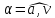 между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени?
между направлением вектора полного
ускорения и вектора скорости частицы
в конечный момент времени?
-
1) Частица, имея начальную скорость
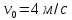 ,
движется прямолинейно с отрицательным
ускорением, модуль которого зависит
от ее скорости по закону
,
движется прямолинейно с отрицательным
ускорением, модуль которого зависит
от ее скорости по закону
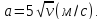 Найдите время движения частицы до
остановки.
Найдите время движения частицы до
остановки.
ЗАДАЧИ К ИНДИВИДУАЛЬНОМУ ДОМАШНЕМУ ЗАДАНИЮ №2
