Соотношение неопределенностей Гейзенберга.

Для любых волн 1).

- неопределенность координаты

- неопределенность координаты

- неопределенность координаты

2).

- временная неопределенность.

- частотная неопределенность.

Для волн де Бройля:

1).

, ,- неопределенности координат.

- неопределенности краевых импульсов.

2).

- временная неопределенность.

- неопределенность энергии.

Пример 1. (Пылинка).

.

В макромире можно пользоваться понятием траектории.

Пример 2. (Электрон в атоме).

Метод, который используется в классической механике, не работает при расчете траектории.

БИЛЕТ 42. Временное и стационарное уравнения Шредингера.

«Вывод» уравнения Шредингера.

Плоская волна, вдоль оси .

, ,,

,

,

, где - потенциальная энергия.

Обобщаем

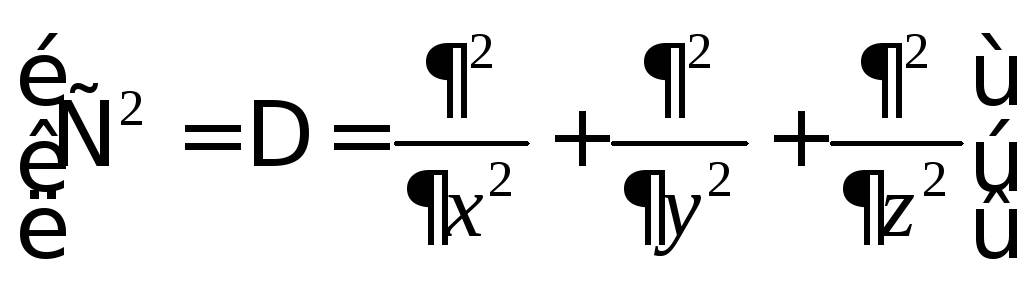
- временное уравнение Шредингера (временное, так как в него

входит полная волновая функция .

Стационарное уравнение Шредингера.

(ищем решение в таком виде).

Примечание:

только если .

Обозначим .

- стационарное уравнение Шредингера.

Оно стационарно, если:

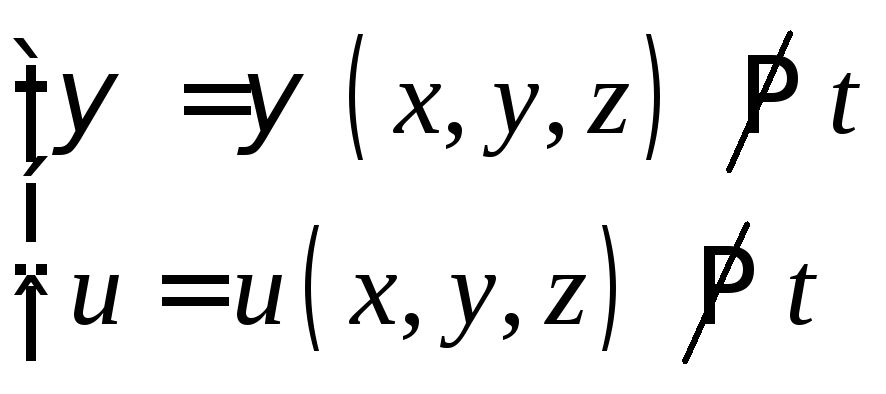(значок означает независимость от).

.

В стационарном случае ,.

Операторная форма:

- решения.

БИЛЕТ 43. Решения уравнения Шредингера для свободного электрона и электрона в потенциальном "ящике".

Пример 1. (свободная частица массой , движущаяся со скоростьювдоль оси).

(свободная частица, нет внешнего силового поля).

(так как движение происходит только вдоль оси)

.

Общее решение- две плоские волны вдоль и вдоль.

В нашем случае

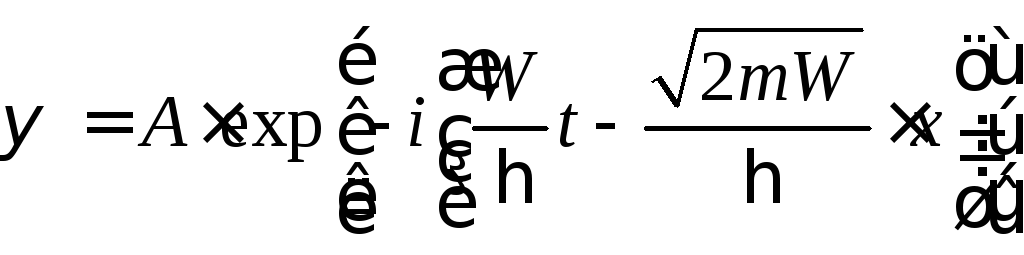
- полная неопределенность координаты и полная ясность с импульсом .

Пример 2. (электрон в потенциальном «ящике» (яме, колодце) ).

, если

, если

, - граничные условия.

Для области II.

Для I и III областей:

.

в уравнении .

, где - целое число.

Физический смысл: (где- длина волны де Бройля).

При приходим к классическому результату.

(с ростом)

при (соответствует классике).

Принцип соответствия Бора:

Любой кванто-механической результат при должен соответствовать классическому.

Любая новая теория в предельных случаях должна соответствовать старой теории.

БИЛЕТ 44. Прохождение частиц сквозь потенциальный барьер (туннельный эффект).

Принцип 3. (Туннельный эффект). (обратить внимание, будут спрашивать на экзамене).

- высота барьера

- ширина барьера

Эффект проникновения частицы за потенциальный барьер в том случае, когда энергия частицы меньше высоты этого барьера().

Это чисто кванто-механический эффект.

- коэффициент прозрачности.

.

БИЛЕТ 45. Линейный гармонический осциллятор. Классическое и квантовое рассмотрение.

Классическое рассмотрение.

,

при

,

Квантовая теория.

,

Следовательно, ,(квантование энергии).

- нулевая энергия (её нельзя отнять осциллятором).

,

принцип соответствия

БИЛЕТ 48. Квантование энергии и момента импульса электрона в атоме. Главное, орбитальное и магнитное квантовые числа. Пространственное квантование.

- главное квантовое число.

- орбитальное квантовое число.

- магнитное квантовое число.

- спиновое квантовое число.

, .

- орбитальный момент импульса электрона.

- - состояние.

- - состояние.

- - состояние.

- - состояние.

- - состояние.

Магнитное квантовое число.

(пространственное квантование).

- орбитальное гиромагнитное отношение

Внешнее магнитное поле вдоль .

, (пространственное квантование).

БИЛЕТ 49. Опыт Штерна и Герлаха. Спин электрона. Спиновое квантовое число.