Добавил:

kaktyss94 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

Теплотехника

Файл:

2_теплообмен (УЭИ_2016)

.pdf

Скачиваний:

Добавлен:

22.06.2019

Размер:

1.6 Mб

Скачать

☆

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Жидкости имеют коэффициент теплопроводности примерно от 0,01 до 0,9 Вт/(м К). Коэффициент теплопроводности воды составляет примерно вод =

0,6 Вт/(м К).

Строительные материалы имеют коэффициент теплопроводности примерно от 0,1 до 10 Вт/(м К). Коэффициент теплопроводности силикатного

кирпича к = 0,8	Вт/(м К).
Самыми теплопроводными материалами являются металлы. Наибольшим
коэффициентом теплопроводности примерно равным				с = 400	Вт/(м К)	обла-
дают серебро и медь.
		Органические газы и пары
		Аморфные изоляционные материалы
		Масла
			Неорганические газы и пары
			Органические жидкости
			Неорганические жидкости
			Неорганические водные растворы
			Органические водные растворы
			Порошки
				Огнеупоры
					Кристаллы
			Жидкие металлы
		Технические сплавы металлов
			Чистые металлы
0,0015	0,015	0,15	1,5	15	150	1500
			, Вт/(м.К)

Рисунок 2.1 - Значения коэффициентов теплопроводности различных веществ

2.2 Дифференциальное уравнение теплопроводности

Основная задача теории теплопроводности состоит в определении температурного поля t = f(х, у, z, ) в твердом теле с учетом процессов, происходящих на его внешних границах.

Выведем уравнение теплопроводности, описывающее процесс переноса теплоты теплопроводностью в пространстве и времени. Допущения, используемые при выводе:

а) внутренние источники теплоты отсутствуют; б) рассматриваемое тело изотропно, т.е. обладает одинаковыми физиче-

скими свойствами по всем направлениям.

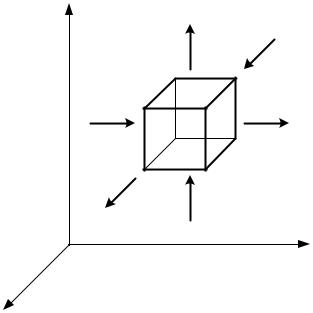
Рассмотрим элементарный объем dV = dx dy dz (рисунок 2.2). Согласно закону сохранения энергии, разность между количеством теплоты, входящей вследствие теплопроводности в этот элементарный объем dV за время d и вышедшей из него за это же время, расходуется на изменение внутренней энергии (т.е. на нагрев) рассматриваемого элементарного объема.

z
		dQz2	1
			Q y
			d
dQx1		dz	dQx2
	y	dz
	y
	d	dx
2		dx
2
Q y
d		dQz1
		dQz1
			x

Рисунок 2.2 - К выводу уравнения теплопроводности

Рассмотрим перенос теплоты в направлении z.

Количество теплоты, входящее в элементарный объем dV по направлению z, согласно закону Фурье, равно:

		t
δQz1	= −λ dx dy dτ

		z .	(2.2)

Количество теплоты, покидающее элементарный объем dV по направлению z, равно

δQ

= −λ dx dy dτ

(t + dt)= −λ

dx dy dτ

t +

= −λ dx dy dτ

− λ dx dy dτ

dz.

(2.3)

Количество теплоты, расходуемое на нагрев элементарного объема по направлению z, равно

δQ

= δQ

− δQ

+ λ dx dy dτ

= −λ dx dy dτ

+ λ dx dy dz dτ

= λ dV dτ

(2.4)

Совершенно аналогично можно получить количество теплоты, расходуемое на нагрев элементарного объема dV по направлению x, оно равно

δQ	x

		2	t
		2
= λ dV dτ	x		2
	x

(2.5)

а количество теплоты, расходуемое на нагрев элементарного объема dV по направлению y, равно

				t
			2
δQ	y	= λ dV dτ	y	2 .	(2.6)
	y			2 .	(2.6)

Суммарное количество теплоты, расходуемое на нагрев элементарного объема dV по всем направлениям, равно

								2	t
								2
δQ = δQ	x	+ δQ	y	+ δQ	z	= λ dV dτ			2
	x		y		z		x		2
							x

		2	t
		2
+	y		2
	y

+2 tz2

  

(2.7)

Выражение в скобках представляет собой оператор Лапласа от температурного поля. По определению оператор Лапласа или лапласиан от произвольной функции равен квадрату градиента:

				2				2				2
=	2	=	x			+	y			+	z
	2
					2				2				2
					2				2				2

То есть можно записать:

δQ = λ dV dτ Δt .

(2.8)

(2.9)

С другой стороны, согласно первому закону термодинамики, в изохорном процессе вся подводимая теплота к элементарному объему dV идет на увеличение его внутренней энергии dU:

	δQ = dU = c		dm dt = c			ρ dV			t	dτ	,
	δQ = dU = c	v	dm dt = c		v	ρ dV			τ	dτ
		v			v

где dm – масса элементарного объема dV, dm = dV;
сv	– теплоемкость при V = const, для твердого тела сv = ср = с;
	– плотность тела, кг/м3;
dt	– изменение температуры за время d :			dt =			t	dτ	.
				dt =			τ	dτ

Приравняв (2.9) и (2.10), получим

(2.10)

t	=	λ	Δt
τ	=	c ρ	Δt
τ		c ρ

(2.11)

Это и есть дифференциальное уравнение теплопроводности (уравнение Фурье) нестационарного температурного поля, которое удобнее запи-

сывать так:

tτ

Δt		,
Δt

(2.12)

где а = /(с ) – коэффициент температуропроводности тела, м2/с.

Это физическая величина, характеризующая скорость изменения температуры в теле и его теплофизические свойства; зависит от природы вещества и его физического состояния.

В цилиндрической системе координат уравнение Фурье выглядит следующим образом:

t		2	t		1 t		1		2	t			2	t
		2							2				2
	= a		2	+		+		2		2	+
			2					2		2				2	.
τ	r				r r		r					z			.
τ	r				r r		r					z

При наличии в твердом теле внутренних источников теплоты qv ние (2.10) примет вид:

(2.13)

уравне-

t	= a Δt +	qv
τ	= a Δt +	ρ c	.	(2.14)
τ		ρ c	.	(2.14)

Условия однозначности

Уравнение Фурье является дифференциальным уравнением второго порядка и поэтому имеет бесконечное множество решений вида t = f(x, y, z, , C1, C2), где С1 и С2 – константы интегрирования, которые в общем случае могут принимать любые значения.

Для того чтобы выбрать единственное необходимое решение для данного конкретного случая, необходимо задать условия однозначности.

Условия однозначности:

1геометрические условия - задаются форма и размеры рассматрива-

емого тела;

2временные условия - ограничивают процесс по времени;

3физические условия - теплофизические свойства веществ;

4граничные условия - состоят в задании условий теплообмена на границах тела с внешней средой.

Граничные условия могут быть заданы тремя способами:

- граничные условия первого рода - задается распределение температур на поверхности тела для каждого момента времени:

при х = хгр

t = f(xгр, ),

- граничные условия второго рода - задается поверхностная плотность теплового потока в каждой точке поверхности тела для любого момента времени:

при х = хгр

q = f(xгр,),

- граничные условия третьего рода - задается температура среды, окру-

жающей тело, и закон теплоотдачи между поверхностью тела и окружающей средой:

при х =хгр

- ·

(dt/dx)	x=x
	гр

= α(t	гр

− t	с	)
	с

2.3 Теплопроводность при стационарном режиме 2.3.1 Теплопроводность плоской стенки

Однослойная плоская стенка. Рассмотрим однородную стенку толщиной d (рисунок 2.3, а), коэффициент теплопроводности которой постоянен и равен . Температура изменяется только в направлении оси х, а изотермические поверхности располагаются перпендикулярно этой оси. Внутренние источники тепла в стенке отсутствуют. На наружных поверхностях поддержива-

ются температуры tc1 и tc2, т.е., граничные условия первого рода выглядят следующим образом:

tc1

q tc2

х = 0		t = t	с1	,

	х = δ	t = t		.
			с2

t
		2	3
1		2	3
tc1	t
	t
	c2

(2.15)

tc3

0	x				tc4
	x
	dx	x
	dx	x
	d	d1	d2	d3	x
					x

	а		б

а) однослойная стенка; б) многослойная стенка Рисунок 2.3 - Теплопроводность через плоскую стенку

Выделим на расстоянии х слой толщиной dx, ограниченный двумя изотермическими поверхностями. На основании закона Фурье (уравнение (2.1)) для этого слоя можно написать

q = −λ	dt	или dt = − q dx .
	dx
		λ

В результате интегрирования этого уравнения имеем

(2.16)

t = −	q	x + C .	(2.17)

	λ

Это - уравнение прямой линии. Значит, распределение температур в однородной плоской стенке при = const – линейное (рисунок 2.3, а).

Константа интегрирования С определяется из граничного условия: при х

= 0 t = tc1, откуда С = tc1.

Так как при х = d t = tc2, то

t		= −	q
t	c2	= −	λ
	c2

Из этого уравнения определяется теплового потока q, а именно:

δ + t	c1	.	(2.18)


значение			поверхностной плотности

q =

− t

Δt

Вт/м .

(2.19)

t = t с1 − t с2

где

, причем всегда t с1

> t с2 ;

R = d/ – внутреннее термическое сопротивление теплопроводности стенки, (м2 К)/Вт.

Из уравнения (2.17) легко получить функцию распределения температуры в однородной плоской стенке:

t =	t	c2	− t	c1	x
t =					x

			δ

(2.20)

Встационарных условиях, когда энергия не расходуется на нагрев, плотность теплового потока неизменна по толщине стенки q = сonst.

Вбольшинстве практических задач приближенно предполагается, что ко-

эффициент теплопроводности

не зависит от температуры и одинаков по

всей толщине стенки. Значение

находят в справочниках при средней темпе-

ратуре

cр

= 0,5 (t

с1

+ t

с2

)

Тепловой поток через однородную плоскую стенку площадью F опреде-

ляется по формуле

Q = q F =

(t с1 − t с2 ) F , Вт.

(2.21)

Тепловой поток всегда направлен в сторону уменьшения температур, как показано на рисунке 2.3.

Многослойная плоская стенка. Пусть стенка состоит из трех разнородных, плотно прилегающих друг к другу слоев (рисунок 2.3, б). Толщина равна: первого слоя d1, второго слоя d2 и третьего слоя d3. Соответственно коэффици-

енты теплопроводности слоев равны 1, 2 и 3. Температуры наружных поверхностей стенки: tc1 и tc4, температуры на границах раздела слоев внутри стенки: tc2 и tc3. Благодаря хорошему контакту между слоями соприкасающиеся поверхности имеют одну и ту же температуру.

При стационарном режиме поверхностная плотность теплового потока постоянна и для всех слоев одинакова. Поэтому на основании формулы (2.19) для каждого слоя можно написать

	λ	1	(t		− t			);
q =		1	(t	c1	− t	c2		);
	δ			c1		c2
	δ	1
		1
	λ	2	(t		− t			);
q =		2	(t	c2	− t		c3	);
	δ			c2			c3
	δ	2
	λ	3	(t					).
q =	λ	3	(t		− t			).
	δ			c3			c4
	δ			c3			c4
		3

(2.22)

Из этих уравнений легко определить изменение температуры в каждом

слое:

	t	− t		= q	δ		;
	t	− t		= q	1		;
c1					1
c1			c2		λ
					λ	1
						1
		− tc3		= q	δ	2
tc2						2	;
tc2					λ		;
					λ	2
		− tc4		= q	δ	3
tc3						3	.
tc3					λ		.
					λ	3

Просуммировав правые и левые части уравнений (2.23), получим

(2.23)

	δ1		δ2			δ3
t − t = q		+			+
	λ		λ			λ		(2.24)
с1 с4							.
	1			2		3

Значит, плотность теплового потока через трехслойную плоскую стенку

равна

q =

t c1 − t c4

δ1

δ3

δi .

(2.25)

i=1

Обобщая полученный результат на плоскую многослойную стенку с произвольным количеством слоев n, можно записать:

q =	t	c1	− t		c(n+1)		=	Δt
		c1			c(n+1)			Δt
			n	δ				n
			n					n
						i		R λi
						i
				λ
			i=1	λ		i		i=1
			i=1			i		i=1

, Вт/м2,

(2.26)

где n – число слоев многослойной стенки;

tc1 и tc(n+1) - температуры на внешних границах многослойной стенки;

n R λi i=1

- полное термическое сопротивление многослойной плоской

стенки, равное сумме термических сопротивлений всех слоев стенки.

Плотность теплового потока, проходящего через все слои, в стационарном режиме одинакова. А так как коэффициент теплопроводности различен, то для плоской многослойной стенки распределение температур – ломаная линия (рисунок 2.3, б).

Рассчитав тепловой поток через многослойную стенку, можно найти температуру на границе любого слоя. Для k-го слоя из (2.26) можно записать

	k
tc(k+1) = tc1	− q R λi	.
	i=1

2.3.2 Теплопроводность цилиндрической стенки

(2.27)

Однослойная цилиндрическая стенка. Задачу распространения теплоты в цилиндрической стенке удобнее рассматривать в цилиндрических координатах.

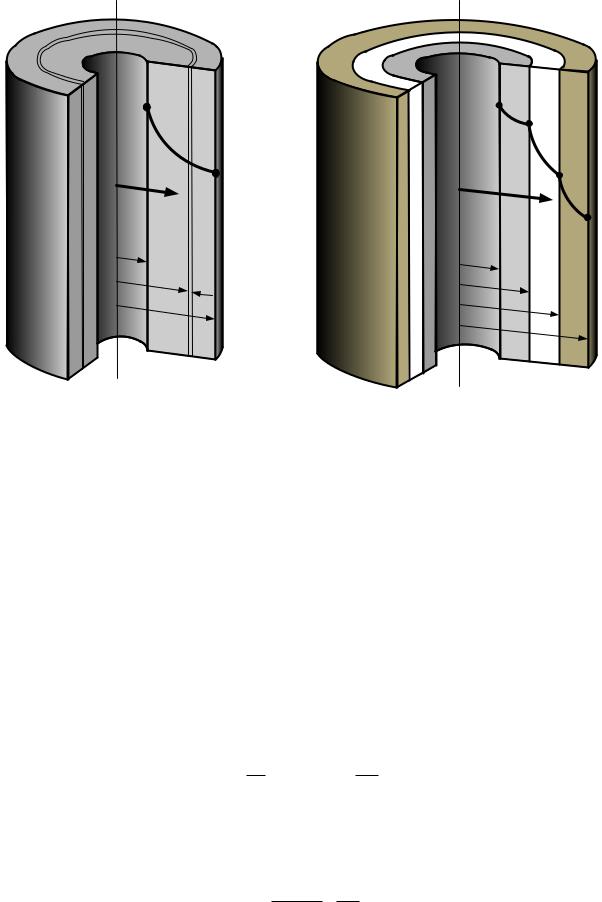
Рассмотрим однородную цилиндрическую стенку (трубу) длиной L, с внутренним радиусом r1 и внешним радиусом r2 (рисунок 2.4, а). Коэффициент теплопроводности материала постоянен и равен . Внутренние источники тепла в стенке отсутствуют. Внутренняя и внешняя поверхности поддерживаются при постоянных температурах tc1 и tc2 причем tc1 > tc2. Температура изменяется только в радиальном направлении. Следовательно, температурное поле здесь будет одномерным, а изотермические поверхности - цилиндрическими, имеющими с трубой общую ось.

tс1

	ql	tс2

	r1
	r	dr
	r2	dr
	r2

tс1	tс2
	tс2
q		tс3
q
l
1	2	tс4
1	2	3
r1
r2
r3
r4

а) однослойная стенка; б) многослойная стенка Рисунок 2.4 - Теплопроводность через цилиндрическую стенку

Выделим в стенке кольцевой слой с радиусом r и толщиной dr. Согласно закону Фурье, тепловой поток, проходящий через такой слой, равен

Q = −λF	dt	= −λ2πrL	dt
				,	(2.28)
	dr		dr

или через линейную плотность теплового потока ql (см. (1.2)):

q	=	Q	= −λ2πr	dt
		L		dr

Разделяем переменные в уравнении (2.29):

dt = − 2πq λ drr .

(2.29)

(2.30)

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете Теплотехника

#
22.06.20194.46 Mб2881. Лекции Термодинамика (УЭИ).pdf
#
22.06.20191.6 Mб862_теплообмен (УЭИ_2016).pdf
#
22.06.2019311.48 Кб54теплотехника.docx