Phedotikov / 1 / FreeEnergy_27.01.08 / !Информация / Nikolo Tesla / Tesla's science of energy

The T-1050 magnetic field detector has a series of amplifying, smoothing elements and notch filters which make for flat response from 0.1 to 50,000 Hz for magnetic

field strengths only detection with a sensitivity of about 10-6 Gauss for the high pass circuit; 0.1 to 200 Hz for the low pass circuit with a sensitivity of 0.5 x 10-10 Gauss.

259

Maxwell's equations are only approximately valid in the ELF region when coil

We present examples of frequency and time domain measurements which lend support to the statements we have just delineated. Figure 1 shows the unusual relationship of a typical sine wave and its representation in the frequency and time domain. Figure 2 is an example of the serpentine-like appearance of the "Russian Woodpecker" in the frequency domain as demodulated by a spectrum analysis. Shown are the 10 Hz pulses on a high frequency "carrier."

Figure 3 is a representation of a magnetic field measurement of about a 30 Hz signal gathered with a coil detection system and displayed on an oscilloscope in the time domain. Although the frequencies are 10 and 30 Hz respectively, the ELF region of interest that they occupy are close enough to note that both of these displays are highly similar and serpentine-like, implying a comparative measurement in the frequency domain; and time domain at higher frequencies do not exist at ELF.

The trace in Figure 4 is generated as a mechanical model of soliton waves generated by the sine-Gordon equation which has periodic soliton solutions. Note the similarity to Figure 3 which is a magnetic signal observed with the T-1050 displayed in the time domain at about 31.5 Hz which can be decomposed into a 30 Hz signal heterodyned with a 1.5 Hz rotational vector. The amplitude is 2 volts/division for a one second trace. Pulse modulation at 3.33 Hz was observed. Normally one would describe this signal as a Heterodyne of 30 Hz and 1.5 Hz but the rotational wave characteristics are better seen in the nonrailed signal in Figure 3, the second trace. The signal in the top trace in Figure 3 is actually a slice in two dimension from a rotational wave in five dimensions or five dimensional rotor or screw wave which is like a five dimensional twister algebra related to a four dimensional spinor calculus.

In Figure 5 is a five dimensional representation of this screw or rotational wave. To represent it in a two dimensional figure on flat paper, we consider amplitude as a

explain the observation seen in Figure 2 and 3 and a great deal of other similar data with the model of the multidimensional soliton wave. Figure 6 is a schematic

Simple solutions to solitary wave equations can be found in terms of the usual conic section form of the trigonometric functions of sines and cosines built on the relationship to the sphere. Simple second order equations generate parabolic and hyperparabolic forms x2 +- y2 = c as contour integration of exponential functions in the complex plane z = x + iy for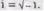

We will examine the properties of Fourier and Laplace transforms and Lorentz invariants conditions and relate these to Gausses' theorem.

and time domain in circular so that more forms observed in the frequency and time domains appear the same. Also consider the envelope on the curve as seen as extended oscillation, in their amplitude dependence or frequency and time, obey sine waves such as x = sin (t/t0) and x = sin (f/f0) contained under the envelope of the curve. Note that in general, the five dimensional travelling wave can be elliptical, having different "periods" or extensions in time and frequency, for example, the

262

[3] W. V. Bise. "Magnetic ELF Comparisons with Acoustic Measurements on Mt. St. Helens" Planetary Association/or Clean Energy 3:1: page 26, June 1981.

[5] E.A. Rauscher and W.L. Van Bise. "Obaervations of Local and Global Earth Ionospheric Excitations for Earthquake and Volcanic Predictions," Bull. Am. Phys. Soc. 32,67,1987; PSRL 17741, October 1986, TRL Report SAn Leandro, CA. 94579

[6] W.V. Bise and E.A. Rauscher: "Non-superconducting Systems for Detecting and Analyzing Low Intensity Pure Magnetic Fields." Tecnic Reearch Laboratories Report, published in Bull Am Phys Soc, Volume 34, p. 109, 1989.

[7] W.V. Bise and E.A. Rauscher: "Geomagnetic Pulsations of the Earth's Magnetosphere." Tecnic Reearch Laboratories Report, PSRL-24125 (1987).

[8] N. Tesla, Patent No. 787,412. April 18, 1905. "Act of Transmitting Electrical Energy Through the Natural Medium" and related patents and papers.

[10]E.A. Rauscher. "Electron Interaction and Quantum Plasma Physics," J. Plasma Physics 2, 517 (1968).

[11]E.A. Rauscher. "Quantized Plasmas" Bull. Amer. Phys. Soc. 15, 1639 (1970).

[12]E.A. Rauscher. "Nonlinear Coherent Modes in MHD-Plasmas," Bull. Am. Phys. Soc. 21,1337(1983).

[13]N. Tesla, The Colorado Springs Notes, published by J. Ratliff, The Tesla Publishing Company, Milbrae, CA 1980.

[16] E.A. Rauscher, "A Unifying Theory of Fundamental Processes," UCRL 20808, June 1971, University of California LBL Press.

[18] Project ELF, formerly refered to as Project Sanguine and Project Seafarer, is reviewed in several issues of Aviation Week and Space Technology and also J.R. Waite "Project Sanguine," Science 178, 272 (1972).

[19] Nikola Tesla: Lectures. Patents. Articles. Belgrade, Yugoslavia: Nikola Tesla Museum, 1956.

[20] K.M.Swezey, "Nikola Tesla," Science 122, 1147,1958.

[21] M. Sugiara and J.P. Heppner, "Electric and Magnetic Fields in the Earth's Environment," American Institue of Physics Handbook. McGraw-Hill Book Company. 1972; Section 5 pages 265-303.

[22] N. Tesla. "The Transmission of Electric Energy Without Wires," Electrical World and Engineer. New York: March 5, 1904.

[23] M.M. Frocht, "Experimental Stress Analysis," Handbook of Physics. McGraw-Hill Book Company, 2nd edition, Part 3, Chapter 6, page 84.

[24] E.V. Condon "Molecular Optics," Part 6, Chapter 6, page 117.

266

[25] J. A S i l v a and G. Lochak. Quanta. New York: McGraw-Hill Books Company 1969. (page 1969)

[26] F.M. Lowry, Optical Rotary Power, London: Longman's, Green & Co, 1935.

[28]H.B. Callen, "The Energy Band Theory of Solids, Part 8, Chapter 8, page 24.

[29]J.C. Anderson, Magnetism and Magnetic Materials: London: Chapman and Hall, Ltd. 1968; Page 199.

[30]E.A. Rauscher "Properties of Nonlinear Coherent Modes in MHD Plasmas and a Possible Solution of the Plasma Combinent Problem," Proceedings of the Tesla

Centennial Symposium (An IEEE Centennial Activity) Editor, E.A. Rauscher, Tesla 1984.

[31] E.A. Rauscher, "Solitary Waves, Coherent Nondispersive Solutions in Complex Minkowski Spaces," Bull. Amer. Phys. Soc. 27 135 (1982).

[33]Aviation Week and Space Technology, page 19, Nov. 8 ,1976.

[34]E.A. Rauscher and W. Van Bise, "Non-Superconducting Apparatus for Detecting Magnetic and Electromagnetic Fields." Patent No. 4,724,390, Issued February 1988.

[35]E.A. Rauscher, W. Van Bise, and H.J. Faretto: "Field survey measurement of the ambient ELF-VLF-LF frequencies and intensities at the Kalish Ranch site and surrounding areas, Kirkland Arizona." Tecnic Reearch Laboratories Report, PSRL-27643, August 1987.

[36]E.A. Rauscher, "Theoretical Examination of Nonlinear Far From Equilibrium Self-Or-

ganizing Phenomena," TRL Report PSRL-103764, Abstract March 1985, Presented at the USPA. July 1985, Dayton, Ohio.

[37]A.C. Scott, "Active and Non-Linear Wave Propagation," Electronics, 1985.

[38]W. Van Bise, "Extremely Low Frequency (ELF) Radio and Magnetic Signals-New Biologic Clues in the Pacific Northwest Environment," N.W. Center for the Study of Man-Ionizing Radiation Report, Feb 1980, Portland, OR.

[39]J. Beal and E.A. Rauscher, "Modern Science Reads the Earth's Electromagnetic

Fields," Invited paper at the University of California at Davis, Symposium co-spon- sored by the Institute for the Study of Natural Systems, September 10,1988.

[40]C. Ramon and E.A. Rauscher, "Super-Luminal Transformations in Complex Minkowski Spaces," Found of Physics 10,661 (1980)

[41]E.A. Rauscher Paper in The Frontiers of Physics (Iceland Conference Proceedings, Reyjavik, Iceland) B.D. Josephson and A. Puharich, Editors, Essentia Research Associates.

[42]E.A. Rauscher, "Complex Coordinate Geometries in General Relativity and Electromagnetism," Bull. Am. Phys. Soc. 23, 84 (1978).

[43]E.A. Rauscher, "Electromagnetic and Non-Linear Phenomena in Complex Minkowski Spaces," Bull. Am. Phys. Soc. 2£, 351 (1983).

update version is in progress.

[45] E.A. Rauscher, "The Earth's Coriolis Force as an Energy Storage and Release Mechanism for Mediating Seismic Activity," ONR Grant through the University of California, Berkeley for (1) modeling systems using multidimensional geometries (2) Modeling seismic activity (1970-1974)

267