
Сист-лін-рівн-ТР-Семіренко-к2
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ МОРСЬКИЙ УНІВЕРСИТЕТ
Кафедра „Вища та прикладна математика”
СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
Типовий розрахунок
Одеса – 2013
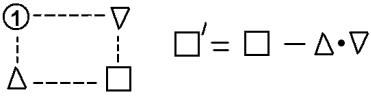
Задача № 1
Розв’язати систему лінійних рівнянь:
а) методом Гауса; б) матричним способом
Приклад розв’язку задачі №1:
Розглянемо спосіб одержати матриці, оберненої до даної за методом послідовних виключень, тобто за допомогою таблиць Гауса.
Дано матрицю
|
1 |
2 |
1 |
|
|
|
|
|
|
A |
3 |
1 |
0 |
. |
|
2 |
0 |
|
|
|
1 |
|||
Матрицю A розміщуємо в лівій частині таблиці, а в правій – одиничну матрицю того самого порядку. Послідовні перетворення виконуємо так, щоб в лівій частині таблиці одержати одиничні стовпці. Якщо на останній ітерації в одиночних стовпцях одиниці містяться на головній діагоналі, то в правій
частині таблиці отримаємо матрицю A 1. Розрахунки виконуємо за формулою
|
aik |
aipaqk |
з використанням схеми: |
|
|||
aik |
aqp |
||
|
|
|
Зауваження: в кожному рядку отримуємо «1» по діагоналі, щоб спростити розрахунки.
Отже, ми отримали обернену матрицю:
|
|
|
1 |
2 |
1 |
|
||
A 1 |
1 |
|
3 |
3 |
3 |
|
||
|
. |
|||||||
|
3 |
|||||||
|
|
2 |
4 |
5 |
|
|||
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
A |
|
|
E |
|
|
|
|
2 |
1 |
1 |
0 |
0 |
|
|
3 |
1 |
0 |
0 |
1 |
0 |
|
|
2 |
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
1 |
0 |
0 |
|
|
0 |
5 |
3 |
3 |
1 |
0 |
|
|
0 |
4 |
3 |
2 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
1 |
0 |
|
0 |
|
0 |
1 |
3 5 |
3 5 |
1 5 |
0 |
||
0 |
4 |
3 |
2 |
0 |
|
1 |
|
|
|
|
|||||
1 0 1 5 |
1 5 2 5 |
0 |
|||||
0 |
1 |
3 5 |
3 5 |
1 5 |
0 |
||
0 0 3 5 |
2 5 1 5 1 |
||||||
|
|
|
|
||||
1 0 1 5 |
1 5 2 5 |
|
0 |
||||
0 |
1 |
3 5 |
3 5 1 5 |
|
0 |
||
0 0 |
1 |
2 3 4 3 |
5 3 |
||||
|
|
|
|||||
1 0 0 |
1 3 2 3 |
1 3 |
|||||
0 |
1 |
0 |
1 |
1 |
|
1 |
|
2 3 |
4 3 |
5 3 |
|||||
0 |
0 |
1 |
|||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
Перевірка:
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
|
|
|
|
|
|
||
1 |
2 |
1 |
|
|
|
|
|
|
|
|
1 |
0 |
0 |
||||||
3 |
3 |
|
3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
1 |
0 |
|
|
1 |
1 |
1 |
|
|
0 |
1 |
0 |
|
|||||
|
2 |
0 |
1 |
|
|
|
2 |
4 |
|
|
5 |
|
|
0 |
0 |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
3 |
|
3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Знайти розв’язок системи:
3
|
|
x y 2z 2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x y 2z 3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x y 4z 1 |
|
|
|
|
|
|
|
|
|
||||||
Матриця системи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
2 |
1 2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4 |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
Матриця – стовпець невідомих: X |
|
|
|
|
|
|
|
|
|
|
||||||
y |
; матриця – стовпець: B |
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
||
Таким чином, маємо: |
A X B, розв’язок системи |
X A 1 B. |
|
|
||||||||||||
Знайдемо A 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
|
|
1 |
|
0 |
0 |
|
|
|
|
||
|
2 |
1 |
2 |
|
|
0 |
|
1 |
0 |
|
|
|
|
|||
|
4 |
|
1 |
4 |
|
|
0 |
|
0 |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
1 |
2 |
|
|
1 |
|
0 |
|
0 |
|
|
|
|
||
|
0 |
|
3 |
2 |
|
|
2 |
1 |
|
0 |
|
|
|
|
||
|
0 |
|
3 |
4 |
|
|
4 |
0 |
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
1 |
2 |
|
1 |
|
|
0 |
|
0 |
|
|
|
|
||
|
0 |
1 |
2 3 |
2 3 |
|
|
1 3 |
0 |
|
|
|
|
||||
|
0 |
3 |
4 |
4 |
|
|
0 |
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
0 |
4 3 |
|
1 3 |
|
|
1 3 |
|
0 |
|
|
|
|
||
|
0 |
1 |
2 3 |
|
2 3 |
|
|
1 3 |
0 |
|
|
|
|
|||
|
0 |
0 |
2 |
|
2 |
|
|
1 |
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
0 |
4 3 |
|
1/ 3 |
|
|
1/ 3 |
|
0 |
|
|
|
|
||
|
0 1 2 3 |
|
2 / 3 1/ 3 |
|
0 |
|
|
|
|
|||||||
|
0 |
0 |
1 |
|
1 |
|
|
1/ 2 |
|
1/ 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||
|
1 0 0 |
|
1 |
1/ 3 2 / 3 |
|
|
|
|
||||||||
|
0 |
|
1 |
0 |
|
0 |
2 / 3 |
|
1/ 3 |
|
|
|
|
|||
|
0 |
|
0 |
1 |
|
1 |
|
1/ 2 |
|
1/ 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
Таким чином: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
6 |
2 |
4 |
|
|
|
|
1 |
6 |
2 |
4 |
2 |
|||||||||
A 1 |
|
0 |
4 |
2 |
; X |
|
|
0 |
|
4 |
2 |
|
|
|
3 ; |
||||||||||
|
|
||||||||||||||||||||||||
|
6 |
|
6 |
3 |
|
|
|
|
|
6 |
|
6 |
3 |
|
|
|
|
|
|||||||
|
|
3 |
|
|
|
|
3 |
|
1 |
||||||||||||||||
x |
|
1 |
12 6 4 |
11 |
; y |
1 |
12 2 |
7 |
; z |
1 |
12 9 3 4. |
||||||||||||||
|
6 |
3 |
|
6 |
|
3 |
|
6 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Перевірка:
113 73 8 2;
223 73 8 3;
443 73 16 1.
Розв’язок системи методом Гаусса:
x |
|
y |
z |
bi |
|
|
|
|
|
1 |
|
1 |
2 |
2 |
2 |
|
1 |
2 |
3 |
4 |
|
1 |
4 |
1 |
|
|
|
|
|
1 |
|
1 |
2 |
2 |
0 |
3 |
2 |
1 |
|
0 |
3 |
4 |
9 |
|
|
|
|
|
|
1 |
|
1 |
2 |
2 |
0 |
|
|
2 3 |
1 3 |
0 |
3 |
4 |
9 |
|
|
|
|
|
|
1 |
|
0 |
4 3 |
5 3 |
0 |
|
1 |
2 3 |
1 3 |
0 |
|
0 |
2 |
8 |
|
|
|
|
|
1 |
0 |
4 3 |
5 3 |
|
0 |
1 |
2 3 |
1 3 |
|
0 |
0 |
|
|
4 |
|
|
|
|
|
1 |
0 |
0 |
1 3 |
|
0 |
1 |
0 |
7 3 |
|
0 |
0 |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
5
Розв’язок системи: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x 11; |
|
|
|
|
|||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
y 7 |
; |
|
|
|
|
||
|
|
|
|
|
|
z |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
||
Простіше всі розрахунки виконувати в одній таблиці: |
|
||||||||||||
x |
y z |
|
A 1 |
bi |
x |
y z |
|
A 1 |
bi |
||||
|
1 |
2 |
1 |
0 |
0 |
2 |
1 |
0 |
4 3 1 3 |
1 3 |
5 3 |
||
2 |
1 |
2 |
0 |
1 |
0 |
3 |
0 |
|
2 3 2 3 |
1 3 |
1 3 |
||
0 |
0 2 2 |
1 |
8 |
||||||||||
4 1 4 |
0 0 1 1 |
||||||||||||
1 |
1 |
2 |
1 |
0 |
0 |
2 |
1 |
0 |
4 3 |
1 3 |
1 3 |
53 |
|
|
|
|
|||||||||||
0 3 |
2 2 1 0 |
1 0 |
1 2 3 2 3 1 3 |
13 |
|||||||||
0 3 |
4 4 |
0 1 9 0 0 |
|
1 |
1 2 |
||||||||
|
|
|
4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
1 1 |
2 |
1 |
|
0 |
2 1 0 0 1 |
1 3 |
11 |
||||||
0 |
|
2 3 2 3 |
1 3 1 3 |
0 |
1 |
0 |
0 2 3 |
3 |
|||||
0 3 |
4 4 |
|
0 |
9 |
1 |
1 2 |
7 |
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
0 |
0 |
1 |
3 |
|||
|
|
|
|
|
|
|
|
|
4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x 11; |
||
|
|
|
A 1 |
1 |
1 3 |
2 3 |
|
3 |
|
||||
Таким чином: |
0 |
2 3 |
1 3 |
|
y 7 |
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
1 3 |
|
1 2 |
|
|
|||
|
|
|
|
|
|
|
z 4. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
12 6 4 |
11 |
; |
|||||||
x |
|
|
|
6 |
2 |
4 |
2 |
|
|
|
|
||||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
3 |
|
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
12 2 |
7 |
|
|
||||
y |
|
|
0 |
4 |
2 |
|
3 |
|
y |
|
|
; |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
6 |
|
6 |
3 |
|
|
|
|
|
|
|
|
6 |
|
3 |
|
|
|
||||
z |
|
|
|
|
3 |
1 |
|
z |
1 |
12 9 3 4. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6
Варіанти:
x 4 y 2z 8
x 5 y 3z 1
1.
4x 6 y z 4.
2x y z 1
4.x 2 y 2z 03x y 4z 1.
x 2 y 4z 1
5x y 2z 1
3x y z 17.
x 2 y 3z 3
5 y z 2
x y 2z 1
4x 2 y 3z 1
x z 2
2.
2x y z 0.
|
x 3y 2z 3 |
|
3x y z 5 |
5. |
3x 5 y 2z 1.
x y 2z 2
8.2x y 2z 34x y 4z 1
2x 3y 6z 17
11.3x 4 y z 3x 5 y 2z 10
2x y z 2
x 2 y 3
x y 1.
x 4 y 2z 33x y z 5
3x 5 y 6z 96.
2x y z 3 9. x y z 42x 2 y z 1
x 4 y 2z 8
x 5 y 3z 1
12.
4x 6 y z 4
7x 2 y 4z 1x 3y 2z 2
13.
x 4 y z 8.
2x 2 y z 6 |
|
|
4x 3y z 3 15. |
14. |
|
x 4 y 2z 9.
x y z 1
15.8x 3y 6z 24x y 3z 3.
2x y z 3 |
2x 3y 2z 4 |
||
|
x y z 4 |
|
3x 2 y z 11 |
16. |
17. |
||
|
|
|
3x 4 y z 7 |
2x 2 y z 1 |
|
||
|
x 3y z 2 |
x 2 y 4z 31 |
|
|
x 4 y 2z 3 |
|
|
18. |
19. 5x y 2z 20 |
||
|
|
|
3x y z 9 |
x 5 y 3z 10 |
|
||
7
x 4 y 2z 3
3x y z 5
20.
3x 5 y 6z 7
3x y 5z 2 23. x 2 y 4z 32x 4 y 3z 1
x 3y z 4 21. 2x y z 02x y z 1
3x 5z 14 y 2z 2
24.
x 3y z 2
8x 3y 6z 2
22.4x y 3z 3x y z 1
3x 2 y 4z 2 |
|
|
x 3y 5z 3 |
25. |
|
|
x 2 y 3z 1 |
|
|
x 2 y 3z 7 |
|
x 2 y 2 |
x y 2z 2 |
||
|
|
|
|
|
2x y 2z 1 |
26. 5x y 2z 7 |
27. 4x 7 y 2z 1 |
28. |
|||
|
3x y z 2 |
|
x 5 y z 2 |
|
|
|
|
4x y 4z 3 |
|||
x 2 y 3z 1
29.2x 3y 4z 13x 2 y 5z 2
x 4 y 2z 3
3x y z 5
3x 5 y 6z 9.
Задача 2
Розв’язати систему методом Гауса:
|
x1 2x2 3x3 4x4 0 |
|||
|
7x1 14x2 20x3 27x4 0 |
|||
|
||||
|
|
|
|
|
5x1 10x2 16x3 19x4 2 |
||||
|
3x 5x 6x 13x 5. |
|||
|
1 |
2 |
3 |
4 |
Розв’язок системи знайдемо за допомогою метода Гауса – таблиць Гауса.
8

x1 |
x2 |
x3 |
|
x4 |
bi |
||
|
2 |
3 |
|
|
4 |
0 |
|
7 |
14 |
20 |
27 |
0 |
|||
5 |
10 |
16 |
19 |
2 |
|||
3 |
5 |
6 |
|
13 |
5 |
||
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
4 |
0 |
|
0 |
0 |
1 |
|
1 |
0 |
||
0 |
0 |
1 |
|
|
1 |
2 |
|
0 1 |
3 1 |
5 1 |
|||||
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
4 |
0 |
|
II. |
0 |
|
3 |
|
1 |
5 |
|
0 |
0 |
1 |
1 |
2 |
|||
|
|||||||
|
0 |
0 |
1 |
1 |
0 |
||
|
|
|
|
|
|
||
|
1 |
0 |
3 |
6 |
10 |
||
III. |
0 |
1 |
3 |
|
1 |
5 |
|
0 |
0 |
|
|
1 |
2 |
||
|
|
|
|||||
|
0 |
0 |
1 |
1 |
0 |
||
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
3 |
4 |
|
IV |
0 |
1 |
0 |
|
2 |
1 |
|
0 |
0 |
1 |
|
1 |
2 |
||
|
|
||||||
|
0 |
0 |
0 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
3 |
4 |
|
V |
0 |
1 |
0 |
|
2 |
1 |
|
0 |
0 |
1 |
|
1 |
2 |
||
|
|
||||||
|
0 |
0 |
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
|
0 |
1 |
|
VI |
0 |
|
0 |
|
0 |
1 |
|
0 |
0 |
1 |
|
0 |
1 |
||
|
|
||||||
|
0 |
0 |
0 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
9
Розв’язок: |
x1 1, |
x2 1, |
x3 1, |
x4 1 |
|
|
|
1 2 3 4 0 |
|
||
|
|
|
20 27 |
0 |
|
|
7 14 |
|
|||
Перевірка: |
|
10 16 19 2 |
|
||
|
5 |
|
|||
|
|
3 5 |
6 13 5. |
|
|
|
|
|
|||
Варіанти завдань: x1 x2 x3 |
x4 |
|
|||
3x1 x2 x3 x4 1 |
||||
|
x1 3x2 x3 x4 1 |
|||
|
||||
1. |
x1 x2 3x3 x4 1 |
|||
|
||||
x x x 3x 1. |
||||
|
1 |
2 |
3 |
4 |
2x1 2x2 x3 x4 4 |
||||
|
4x1 3x2 x3 2x4 6 |
|||
|
||||
3. |
|
|
|
|
8x1 5x2 3x3 4x4 12 |
||||
3x 3x 2x 2x 6. |
||||
|
1 |
2 |
3 |
4 |
2x1 5x2 4x3 x4 20
x 3x 2x 11
1 2 3 4
5.2x1 10x2 9x3 9x4 40
3x1 8x2 9x3 2x4 37.x
x1 4x2 3x3 2x4 1 |
||||
|
x1 |
x3 |
2x4 0 |
|
|
||||
7. |
|
9x2 5x3 2x4 1 |
||
2x1 |
||||
|
2x 7x 7x 6x 2. |
|||
|
1 |
2 |
3 |
4 |
2x1 3x2 11x3 5x4 2 |
|||
|
x1 x2 5x3 2x4 1 |
||
|
|||
2. |
2x1 x2 3x3 2x4 1 |
||
|
|||
x x 3x 4x 3. |
|||
|
1 2 |
3 |
4 |
5x1 3x2 2x3 4x4 3
4x1 2x2 3x3 4 1
4.8x1 6x2 x3 5x4 07x1 3x2 7x3 17x4 3.7x
x1 x2 2x3 4x4 5
4x1 4x3 4 1
6.3x1 x2 2x3 5x4 0x1 3x2 2x3 3x4 1.9x
x1 x2 2x3 4x4 5
4x 4x 1
1 3 4
8.3x1 x2 2x3 5x4 0x1 3x2 2x3 3x4 1.9x
10
