§3 Приклади і вправи

Вправа 3.1. Записати рівняння площини, що проходить через точку перпендикулярно осі .

Розв’язання.

Оскільки площина перпендикулярна осі , то її нормальним вектором є будь-який вектор, паралельний осі , наприклад, . Скористаємось рівнянням . Отримаємо або .

Вправа 3.2. Записати рівняння площини, що проходить через точку і паралельна двом векторам та .

Розв’язання.

Обчислимо векторний добуток . Вектор є ортогональним до векторів і . Таким чином, він перпендикулярний до шуканої площини. Отже, знаючи нормальний вектор цієї площини і точку , через яку вона проходить, скориставшись рівнянням , отримаємо або .

Вправа 3.3. Записати рівняння площини, що проходить через точку перпендикулярно до двох площин та .

Розв’язання.

Нормальні вектори заданих площин та паралельні до шуканої площини. Тому її нормальний вектор є їх векторним добутком. Тобто . Скористаємось рівнянням , одержимо рівняння площини за точкою , через яку вона проходить, та нормальним вектором

або .

Вправа 3.4. Вершини тетраедра знаходяться в точках , , , . Знайти довжину його висоти опущеної з вершини .

Розв’язання.

Запишемо рівняння площини, в якій лежить основа тетраедра - . Скориставшись рівнянням площини, яка проходить через три точки і . Одержимо

або

Розкривши визначник за елементами першого рядка, отримаємо

або .

Знайдемо, довжину висоти тетраедра як відстань від точки до цієї площини за формулою .

.

Вправа 3.5. Знайти кут між площиною та площиною , що відтинає на координатних осях відрізки .

Розв’язання.

Запишемо рівняння площини "у відрізках" за формулою

або .

Нормальними векторами площин і є відповідно та . Знайдемо кут між площинами за формулою .

Отже, .

Вправа 3.6. Записати канонічні і параметричні рівняння прямої яка проходить через точку паралельно прямій .

Розв’язання.

З канонічних рівнянь прямої видно, що її напрямний вектор . Він є напрямним вектором також і для прямої , оскільки . Знаючи точку , що лежить на прямій та напрямний вектор, запишемо канонічні рівняння прямої , а також її параметричні рівняння .

Вправа 3.7. Записати канонічні рівняння прямої .

Розв’язання.

Пряму задано як лінію перетину двох площин, нормальними векторами яких є та . Оскільки пряма лежить в обох площинах, то вона перпендикулярна обом нормальним векторам. Тому її напрямний вектор знайдемо як їх векторний добуток

.

Тепер слід знайти координати однієї точки , що належить прямій. Вони мають задовольняти загальне рівняння прямої тобто є одним з розв’язків системи двох рівнянь з трьома невідомими. Оберемо дві базисні змінні. Нехай це будуть і , оскільки визначник, що складається з коефіцієнтів при них, відмінний від нуля. Дійсно . Надамо тепер довільного значення змінній , наприклад . З одержаної системи рівнянь 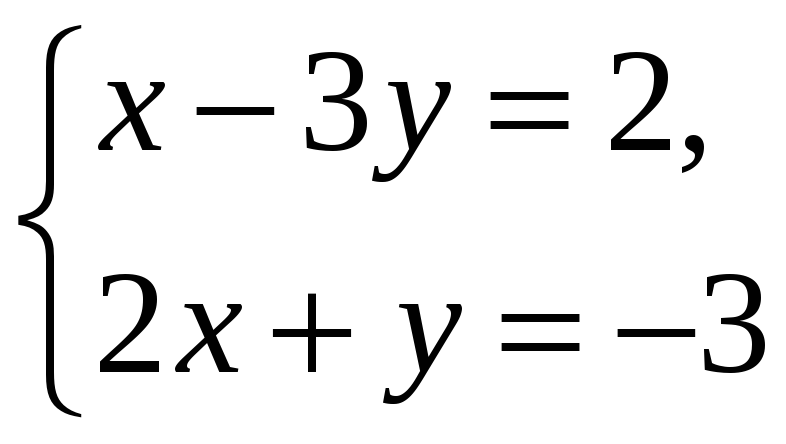маємо . Отже . Таким чином, канонічні рівняння прямої , яка проходить через точку паралельно вектору , мають вигляд .

Вправа 3.8. Записати рівняння прямої, яка проходить через початок координат перпендикулярно до площини .

Розв’язання.

Нормальний вектор площини і шукана пряма паралельні, тобто, вектор є напрямним для цієї прямої. Скориставшись рівнянням і знаючи, що пряма проходить через точку , одержимо рівняння прямої .

Вправа 3.9. Знайти точку перетину прямої і площини .

Розв’язання.

Запишемо параметричні рівняння прямої . Знайдемо таке значення параметру , при якому координати поточної точки прямої задовольняють рівняння площини. Для цього підставимо їх в рівняння площини . З отриманого рівняння знайдемо . Тоді або є точкою перетину прямої і площини.

Вправа 3.10. Обчислити кут між прямою , та площиною .

Розв’язання.

З умови задачі видно, що вектор є напрямним вектором прямої , а - нормальний вектор площини . За формулою маємо

.

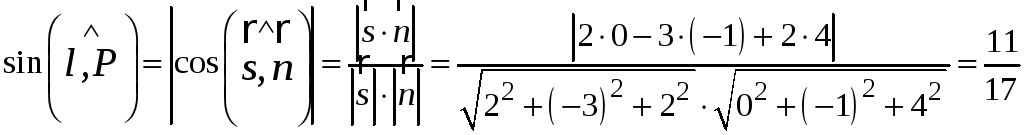Отже .

Вправа 3.11. Довести, що прямі та лежать в одній площині. Написати рівняння цієї площини.

Розв’язання.

Як бачимо з умови задачі, напрямні вектори та прямих і не колінеарні . Тоді прямі і лежать в одній площині лише в тому випадку, якщо вони перетинаються. Візьмемо точки та . Для того, щоб ці прямі лежали в одній площині достатньо, щоб вектори та були компланарні. Тут . Перевіримо компланарність векторів, обчисливши їх мішаний добуток,

. Отже, прямі і перетинаються.

Нормальний вектор шуканої площини ортогональний векторам та . Тому . Знаючи нормальний вектор і точку , яка лежить в площині, запишемо її рівняння за формулою

або .

Вправа 3.12. Знайти проекцію точки на пряму, що проходить через точки та .

Розв’язання.

Напрямним вектором прямої є або будь-який колінеарний йому вектор, наприклад . Запишемо параметричні рівняння прямої за точкою , що належить прямій, та напрямним вектором .

Запишемо рівняння площини , що проходить через точку перпендикулярно прямій , вважаючи нормальним вектором цієї площини. За формулами одержимо

або .

Точка перетину прямої з площиною і є проекцією точки на цю пряму. Щоб знайти точку перетину підставимо координати поточної точки прямої з її параметричних рівнянь у рівняння площини . Маємо

або .

Тоді є координатами шуканої точки. Отже, проекцією точки на пряму є точка .

Вправа 3.13. Точка рухається прямолінійно і рівномірно з положення в напрямі вектора зі швидкістю . Записати рівняння траєкторії руху і визначити, за який час точка пройде відрізок траєкторії, який знаходиться між паралельними площинами і .

Розв’язання.

Рівняння траєкторії записуються як параметричні рівняння прямої , в яких - час, - координати вектора швидкості , - координати початкової точки.

Оскільки , а швидкість , то запишемо рівняння з напрямним вектором і початковою точкою . Маємо

.

Знайдемо спочатку відстань, яку проходить точка вздовж прямої між площинами та . Для цього визначимо точки перетину прямої з кожною з них (див. вправу 3. 9). Одержимо точку перетину прямої з площиною (тут ) і точку перетину цієї прямої з площиною (тут ). Знайдемо відстань між цими точками. Маємо

.

Оскільки швидкість точки , то отриману відстань вона пройде за 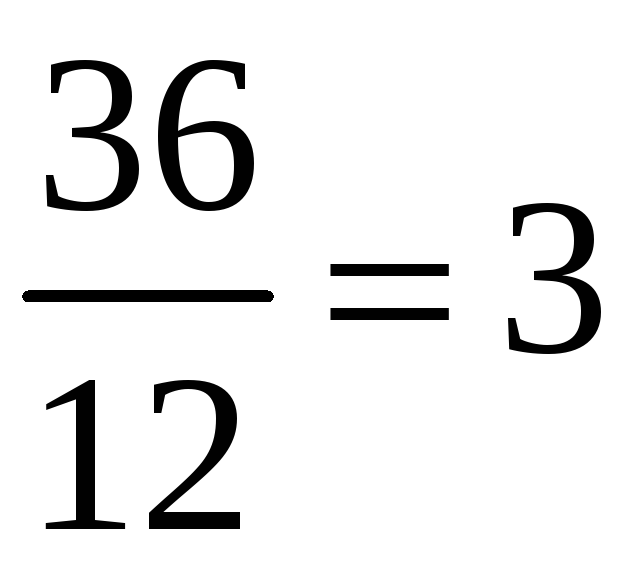одиниці часу.