
- •Г.В. Соколовська с.Ю. Соколовський аналітична геометрія
- •Розділ 1. Пряма лінія на площині
- •§1 Різні види рівняння прямої лінії на площині
- •§2 Основні формули
- •1. Кут між двома прямими. Умови паралельності і перпендикулярності
- •2. Відстань від точки до прямої
- •3. Поділ відрізка в даному відношенні
- •§3 Приклади і вправи
- •Розділ 2. Лінії другого порядку
- •§2 Гіпербола
- •§3 Парабола
- •§4 Приклади і вправи
- •Вправи для самостійного розв’язування
- •Розділ 3. Пряма лінія і площина у просторі
- •§1 Різні види рівняння прямої лінії і площини у просторі
- •1. Різні форми рівняння площини
- •2. Різні форми рівняння прямої у просторі
- •§ 2 Основні формули
- •§3 Приклади і вправи
- •Вправи для самостійного розв’язування
- •Відповіді
Вправи для самостійного розв’язування
Вправа 2.5. Скласти рівняння еліпса, фокуси якого лежать на осі абсцис, симетричні відносно початку координат, якщо
а) його велика вісь дорівнює 20, а відстань між фокусами 24;
б) відстань між фокусами дорівнює 8, а ексцентриситет 0,8.
Вправа 2.6. Скласти рівняння гіперболи, фокуси якої лежать на осі ординат, симетричні відносно початку координат, якщо
а)
асимптоти задані рівняннями
![]() ,
а фокуси знаходяться на відстані
,
а фокуси знаходяться на відстані
![]() від центру;
від центру;
б)
гіпербола має спільні фокуси з еліпсом
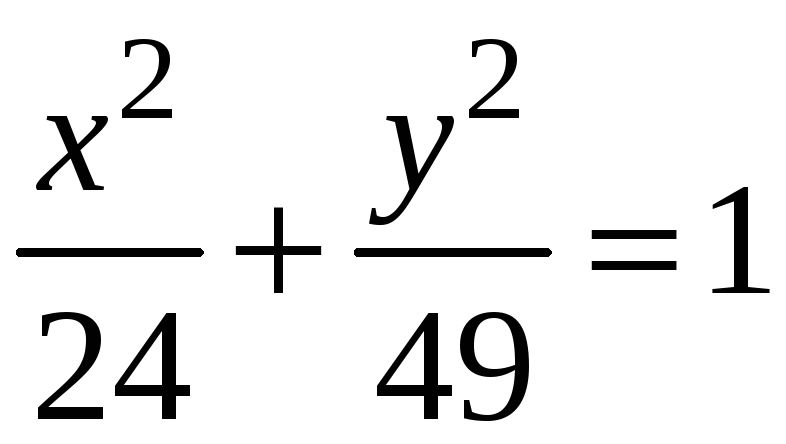 ,
а її ексцентриситет
,
а її ексцентриситет
![]() .
.
Вправа 2.7. Скласти рівняння параболи з вершиною в початку координат, якщо
а)
парабола симетрична відносно осі абсцис
і проходить через точку
![]() ;
;
б)
парабола симетрична відносно осі
ординат, директриса задана рівнянням
![]() .
.
Вправа 2.8. Визначити, яку лінію задає рівняння. Зобразити її на рисунку.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
;
є)
![]() ;
ж)
;
ж)
![]() ;
;
з)
![]() ;
и)
;
и)
 ;
і)
;
і)
![]() .
.
Вправа
2.9. Земля
рухається по еліпсу, в одному з фокусів
якого знаходиться Сонце. Найменша
відстань від Землі до Сонця приблизно
дорівнює
![]() мільйона кілометрів, а найбільша -
мільйона кілометрів, а найбільша -
![]() мільйона кілометрів. Знайти більшу
піввісь та ексцентриситет орбіти Землі.
мільйона кілометрів. Знайти більшу
піввісь та ексцентриситет орбіти Землі.
Вправа
2.10. Дзеркальна
поверхня прожектора утворена обертанням
параболи навколо її осі симетрії. Діаметр
дзеркала
![]() ,
глибина
,
глибина
![]() .
На якій відстані від вершини параболи,
що є осьовим перерізом цієї поверхні,
знаходиться її фокус? Відомо, що
розмістивши у фокусі джерело світла,
отримаємо жмуток паралельних променів.
.
На якій відстані від вершини параболи,
що є осьовим перерізом цієї поверхні,
знаходиться її фокус? Відомо, що
розмістивши у фокусі джерело світла,
отримаємо жмуток паралельних променів.
Розділ 3. Пряма лінія і площина у просторі
§1 Різні види рівняння прямої лінії і площини у просторі
1. Різні форми рівняння площини
1. Рівняння
площини, що проходить через точку
![]() перпендикулярно векторові
перпендикулярно векторові
![]() ( його називають нормальним вектором
площини)
( його називають нормальним вектором
площини)
![]() .
.
![]()
2.
Розкривши дужки у рівнянні
![]() ,
отримаємо загальне рівняння площини
,
отримаємо загальне рівняння площини
![]() .
.
![]()
3. Рівняння
площини, яка проходить через 3 задані
точки
![]() ,
,
![]() ,
,
![]()
 .
.
![]()
4. Рівняння
площини, яка проходить через точки
![]() ,
,
![]() ,
,
![]() ,
або рівняння «у відрізках»
,
або рівняння «у відрізках»
 .
.
![]()
2. Різні форми рівняння прямої у просторі
1. Загальне рівняння. Пряму задають, як лінію перетину двох площин

![]()
2. Канонічні рівняння – це рівняння прямої, що проходить через точку
![]() паралельно
векторові
паралельно
векторові
![]() ( його називають напрямним вектором
прямої)
( його називають напрямним вектором
прямої)
 .
.
![]()
3. Якщо
в рівняннях
![]() позначити через
позначити через
![]() коефіцієнт пропорційності, що дорівнює
кожному з відношень, то вони будуть
еквівалентні трьом рівнянням
коефіцієнт пропорційності, що дорівнює
кожному з відношень, то вони будуть
еквівалентні трьом рівнянням
![]() .
.
![]()
4. Рівняння
прямої, що проходить через 2 задані точки
![]() ,
,
![]()
 .
.
![]()
§ 2 Основні формули
1. Кут між двома площинами
Один з
лінійних кутів між площинами
![]() та
та
![]() дорівнює куту між їх нормальними
векторами
дорівнює куту між їх нормальними
векторами
![]() та
та
![]() .
Тому
.
Тому
 .
.
![]()
2. Кут між двома прямими. Умови паралельності і перпендикулярності
Кут між
двома прямими
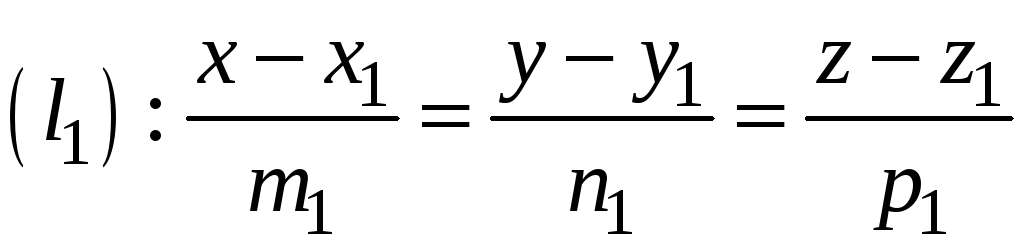 та
та
 визначається як кут між їх напрямними
векторами
визначається як кут між їх напрямними
векторами
![]() та
та
![]() за формулою
за формулою

![]()
Умовою паралельності прямих є колінеарність їх напрямних векторів
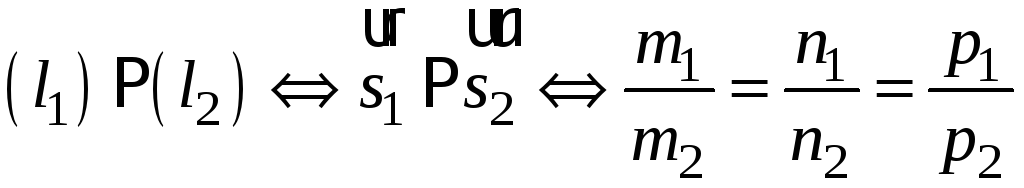 .
.
![]()
Умовою перпендикулярності прямих є ортогональність їх напрямних векторів
![]() .
.
![]()
3. Кут між прямою та площиною. Умови паралельності і перпендикулярності
Кут між
прямою
 та площиною
та площиною
![]() визначається за формулою
визначається за формулою
 .
.
![]()
Умовою паралельності прямої і площини є ортогональність напрямного вектора прямої і нормального вектора площини
![]() .
.
![]()
Умовою перпендикулярності прямої і площини є колінеарність напрямного вектора прямої і нормального вектора площини
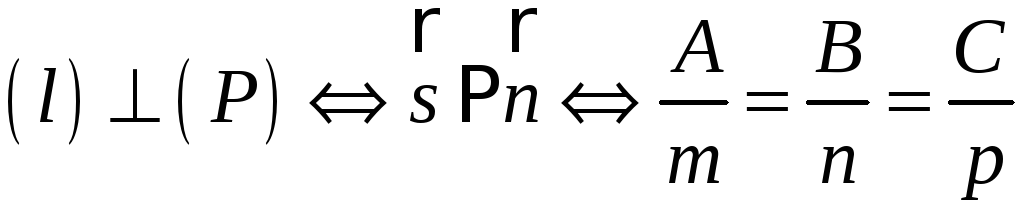 .
.
![]()
4. Відстань від точки до площини
Відстань
![]() від точки
від точки
![]() до площини
до площини
![]() обчислюється за формулою
обчислюється за формулою
 .
.
![]()
