§4 Приклади і вправи

Вправа 2. 1. Записати рівняння еліпса, фокуси якого знаходяться на осі , симетричні відносно початку координат. Точка лежить на еліпсі, відстань між директрисами дорівнює 10.

Розв’язання.

Скористаємось рівнянням і рисунком . Оскільки точка належить еліпсу, то її координати задовольняють рівняння , де . Отже, 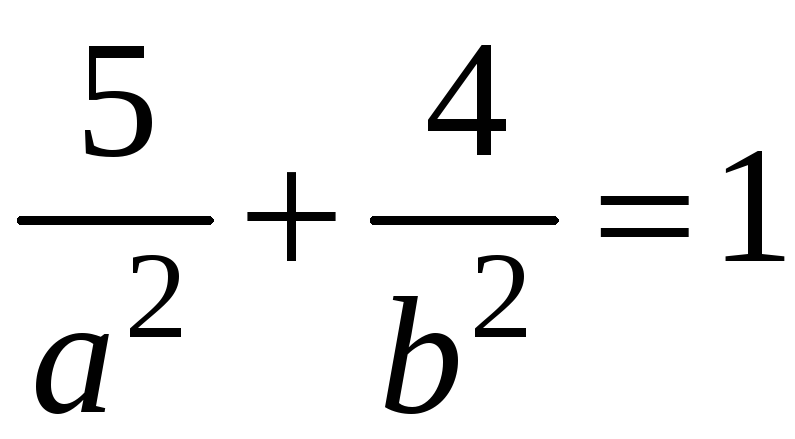або . Відстань між директрисами дорівнює . Враховуючи, що , з останньої рівності маємо або .

Таким чином, утворилась система рівнянь Розв’язавши яку, маємо . Тоді .

Рівняння еліпса має вигляд .

Вправа 2.2. Записати рівняння гіперболи, фокуси якої знаходяться на осі ординат і симетричні відносно початку координат, якщо рівняння асимптот мають вигляд , а відстань між вершинам дорівнює 48.

Розв’язання.

Скористаємось рівнянням , в якому . З рівняння асимптот отримаємо .

Таким чином, рівняння гіперболи має вигляд .

Вправа 2.3. Записати рівняння параболи, знаючи, що вона симетрична відносно осі і проходить через точку , а її вершина знаходиться у початку координат.

Розв’язання.

Канонічне рівняння параболи, симетричної відносно осі має вигляд . Підставивши в нього координати точки , маємо або . Отже, шукане рівняння параболи має вигляд .

Вправа 2.4. Визначити, яку лінію задає рівняння. Зобразити її на рисунку.

а) ; б) ;

в) ; г) ;

д) ; е) ; є) .

Розв’язання.

а) Згрупуємо доданки з та окремо. Доповнимо кожен з отриманих виразів до повного квадрату двочлена.

.

В останньому рівнянні перейдемо до нових змінних за формулами , . Таке перетворення з геометричної точки зору означає паралельне перенесення системи координат. Отримаємо рівняння , що є канонічним рівнянням еліпса з центром в точці або та півосями . Тобто, одержано рівняння кола радіуса , центр якого в системі координат знаходиться в точці . Виконаємо креслення (рис.14).

б) Виконаємо аналогічні перетворення.

.

В останньому рівнянні перейдемо до нових змінних за формулами , . Отримаємо канонічне рівняння еліпса .

В останньому рівнянні перейдемо до нових змінних за формулами , . Отримаємо канонічне рівняння еліпса . В системі координат центр еліпса знаходиться в точці , півосі . Як бачимо, . Тому фокуси цього еліпса (рис.15) знаходяться на осі на відстані від його центру. Позначимо їх та .

в)

.

В останньому рівнянні перейдемо до нових змінних за формулами , . Отримаємо канонічне рівняння гіперболи .

В системі координат центром гіперболи є точка , півосі . Вершини гіперболи знаходяться на осі . Фокуси та знаходяться на цій же осі на відстані від центру. Гіперболу зображено на рис.16.

г)

.

Перейдемо до нових змінних за формулами , . Отримаємо канонічне рівняння гіперболи . В системі координат центром гіперболи є точка , півосі . Зробимо креслення (рис.17).

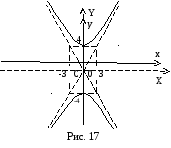
Фокуси гіперболи , та її вершини знаходяться на осі . Відстань від центру до фокуса .

д)

.

Перейдемо до нових змінних за формулами , . Отримаємо канонічне рівняння параболи . В системі координат її вершина знаходиться в точці і парабола розміщується у верхній півплощині відносно прямої . Оскільки або , то фокус знаходиться на осі на вище за вершину. Директриса перпендикулярна осі і перетинає її в точці, що знаходиться на нижче за вершину. Для схематичної побудови параболи використаємо той факт, що точки і (рис. 18), що лежать на прямій, яка проходить через точку паралельно директрисі, і знаходяться на відстані від фокуса, належать параболі (адже відстань від кожної з них до фокуса та до директриси однакова).

е) Рівняння задає лінію, точки якої мають задовольняти умови

Піднесемо до квадрату обидві частини рівняння. Одержимо

. Після заміни , , отримаємо канонічне рівняння еліпса .

Але не всі точки еліпса належать лінії, що задана рівнянням , а лише ті, що задовольняють умови . Зауважимо, що умова виконана для всіх точок еліпса, адже . Умова рівносильна . Вона виконується лише для таких точок еліпса, що знаходяться на осі і праворуч від неї. Отже шукана лінія є правою половиною еліпса. Зробимо креслення (рис.19).

Ф окуси цього еліпса та знаходяться на осі на відстані від його центру .

є) Рівняння задає лінію, для точок якої виконано умови

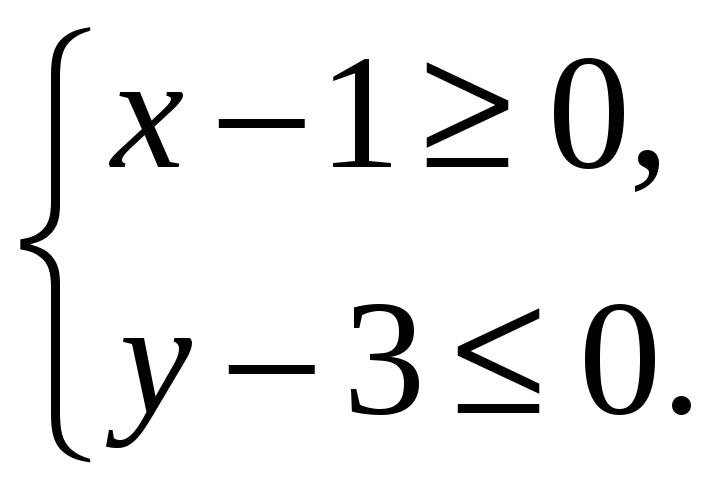
П іднесемо до квадрату обидві частини рівняння. Маємо або , де . Зобразимо параболу, яку задано отриманим рівнянням (рис 20).

Точка - вершина параболи, , . Враховуючи умови або , одержимо тільки нижню відносно осі половину параболи.