Розділ 2. Лінії другого порядку

§1 Еліпс

Означення. Еліпсом називається геометричне місце точок площини, для яких сума відстаней до двох фіксованих точок та цієї площини (що називаються фокусами) є величина стала (вона позначається ). Ця величина більша, ніж відстань між фокусами . Отже, .

Якщо осі прямокутної декартової системи координат вибрано так, що фокуси еліпса знаходяться на осі і симетричні відносно початку координат, то рівняння еліпса має вигляд

,

д е . Рівняння називають канонічним рівнянням еліпса.

Розглянемо еліпс, зображений на рис.11. Точки називають вершинами, - центром еліпса. та відповідно великою і малою півосями. Нехай - довільна точка еліпса. Відрізки та називають фокальними радіусами. Число , називають ексцентриситетом. Якщо (або ), то фокуси співпадають один з одним та з центром. Такий еліпс є колом радіуса . Прямі та називають директрисами еліпса.

§2 Гіпербола

Означення. Гіперболою називається геометричне місце точок, для яких різниця відстаней до двох фіксованих точок та площини (що називаються фокусами) є величина стала (що дорівнює ). Якщо , то . Якщо осі прямокутної декартової системи координат вибрано так, що фокуси гіперболи знаходяться на осі і симетричні відносно початку координат, то рівняння гіперболи має вигляд

,

де . Рівняння називають канонічним рівнянням гіперболи.

Р озглянемо гіперболу, зображену на рис.12. Точки називають вершинами, - центром гіперболи. та відповідно дійсною та уявною півосями. Якщо - довільна точка гіперболи, то відрізки та називають її фокальними радіусами. Число , де - відстань від центру гіперболи до її вершини, називають ексцентриситетом , а прямі та 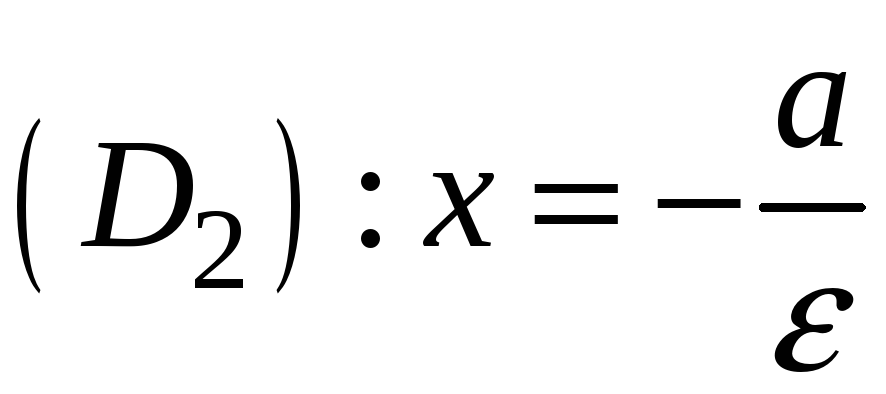- директрисами. Прямі та називають асимптотами гіперболи.

Зауважимо, що гіпербола може також задаватись канонічним рівнянням

,

Фокуси і вершини такої гіперболи знаходяться на осі і симетричні відносно початку координат. Різниця відстаней від будь-якої точки гіперболи до її фокусів дорівнює .

§3 Парабола

Означення. Параболою називається геометричне місце точок, кожна з яких рівновіддалена від фіксованої точки (що називається фокусом) і деякої фіксованої прямої (директриси).

Введемо прямокутну декартову систему координат так, щоб вісь абсцис проходила через фокус параболи перпендикулярно до директриси. Спрямуємо її від директриси до фокуса, а початок координат розмістимо посередині між фокусом та директрисою (рис 13).

В цій системі координат канонічне рівняння параболи має вигляд

,

де . Фокусом такої параболи є точка , а директрисою - пряма . Парабола в цьому випадку лежить в правій півплощині відносно осі і має одну вісь симетрії . Її називають віссю параболи. З нею парабола перетинається в одній точці , яку називають вершиною параболи.

Якщо вершина параболи знаходиться у початку координат, віссю симетрії є вісь абсцис, але парабола розміщена в лівій півплощині відносно осі , то вона задається рівнянням . Якщо вісь параболи суміщена з віссю ординат, а вершина - з початком координат, то рівняння параболи має вигляд

.