
- •Г.В. Соколовська с.Ю. Соколовський аналітична геометрія
- •Розділ 1. Пряма лінія на площині
- •§1 Різні види рівняння прямої лінії на площині
- •§2 Основні формули
- •1. Кут між двома прямими. Умови паралельності і перпендикулярності
- •2. Відстань від точки до прямої
- •3. Поділ відрізка в даному відношенні
- •§3 Приклади і вправи
- •Розділ 2. Лінії другого порядку
- •§2 Гіпербола
- •§3 Парабола
- •§4 Приклади і вправи
- •Вправи для самостійного розв’язування
- •Розділ 3. Пряма лінія і площина у просторі
- •§1 Різні види рівняння прямої лінії і площини у просторі
- •1. Різні форми рівняння площини
- •2. Різні форми рівняння прямої у просторі
- •§ 2 Основні формули
- •§3 Приклади і вправи
- •Вправи для самостійного розв’язування
- •Відповіді
2. Відстань від точки до прямої
Відстань
![]() від точки
від точки
![]() до прямої
до прямої
![]() (рис. 6) можна обчислити за формулою
(рис. 6) можна обчислити за формулою
 .
.
![]()
З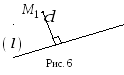 ауважимо,
що знак виразу
ауважимо,
що знак виразу
![]() є однаковим для всіх точок, що лежать в
одній півплощині відносно прямої.
є однаковим для всіх точок, що лежать в
одній півплощині відносно прямої.
3. Поділ відрізка в даному відношенні
Нехай
точка
![]() ділить відрізок
ділить відрізок
![]() (де
(де
![]() ,
,
![]() )
так, що
)
так, що
 .
.
Координати
точки
![]() можна
знайти за формулою
можна
знайти за формулою
 .
.
![]()
Зокрема,
при
![]() маємо координати середини відрізка
маємо координати середини відрізка
![]()
 .
.
![]()
§3 Приклади і вправи
Вправа
1.1. Записати
рівняння прямої, яка проходить через
точки
![]() та
та
![]() .
.
Розв’язання.
Скористаємось
рівнянням
![]() .
Одержимо канонічне рівняння прямої
.
Одержимо канонічне рівняння прямої

або
рівносильне йому загальне рівняння
![]() .
.
Вправа
1.2. Записати
рівняння прямої
![]() ,
що проходить через точку
,
що проходить через точку
![]() паралельно до даної прямої.
паралельно до даної прямої.
Розв’язання.
1) Нехай
пряму задано загальним рівнянням
![]() і
і
![]() .
Нормальний вектор прямої
.
Нормальний вектор прямої
![]() знаходимо з її загального рівняння
знаходимо з її загального рівняння
![]() .
Оскільки пряма
.
Оскільки пряма
![]() ,
то її нормальний вектор
,
то її нормальний вектор
![]() .
Нехай
.
Нехай
![]() .
Тоді, скориставшись рівнянням
.
Тоді, скориставшись рівнянням
![]() ,
одержимо
,
одержимо
![]() або
або
![]() .
.
2) Нехай
маємо точку
![]() і
пряму, яку задано канонічним рівнянням
і
пряму, яку задано канонічним рівнянням
 або
параметричними рівняннями
або
параметричними рівняннями
 .
.
Пряма
![]() ||
||![]() ,
тоді її напрямний вектор
,
тоді її напрямний вектор
![]() .
Нехай
.
Нехай
![]() .
Тоді, скориставшись рівняннями
.
Тоді, скориставшись рівняннями
![]() ,
одержимо
,
одержимо
 або
або
 .
.
3) Нехай
маємо точку
![]() і пряму, яку задано рівнянням з кутовим
коефіцієнтом
і пряму, яку задано рівнянням з кутовим
коефіцієнтом
![]() .
.
Оскільки
пряма
![]() ||
||![]() ,
то їх кутові коефіцієнти рівні, тобто
,
то їх кутові коефіцієнти рівні, тобто
![]() .
Скориставшись рівнянням
.
Скориставшись рівнянням
![]() ,
маємо
,
маємо
![]() або
або
![]() .
.
Вправа
1.3. Записати
рівняння прямої
![]() ,
яка проходить через точку
,
яка проходить через точку
![]() перпендикулярно до даної прямої.
перпендикулярно до даної прямої.
Розв’язання.
1) Нехай
пряму задано загальним рівнянням
![]() і
і
![]() .
Нормальний вектор прямої
.
Нормальний вектор прямої
![]() знаходимо
з її загального рівняння
знаходимо
з її загального рівняння
![]() .
Оскільки пряма
.
Оскільки пряма
![]() ,
то її напрямний вектор
,
то її напрямний вектор
![]() ,
нехай
,
нехай
![]() .
Тоді, скориставшись рівнянням
.
Тоді, скориставшись рівнянням
![]() ,
одержимо
,
одержимо
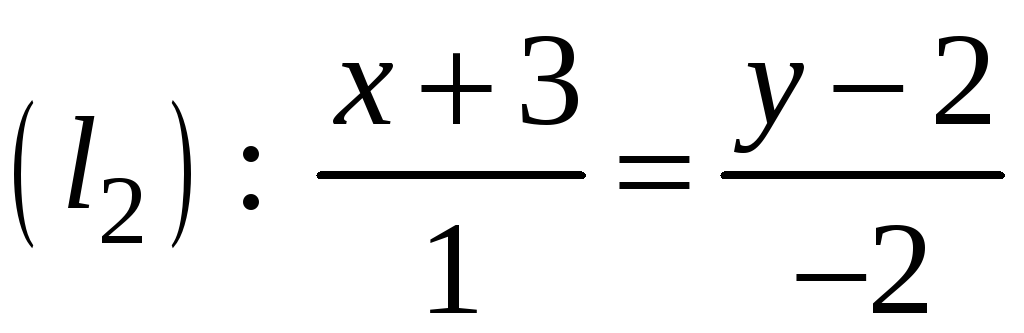 або
або
![]() .
.
2) Нехай
маємо точку
![]() і пряму, яку задано канонічним рівнянням
і пряму, яку задано канонічним рівнянням
 .
.
Оскільки
![]() ,
то її нормальний вектор
,
то її нормальний вектор
![]() ,
де
,
де
![]() - напрямний вектор прямої
- напрямний вектор прямої
![]() .
Візьмемо
.
Візьмемо
![]() і, скориставшись рівнянням
і, скориставшись рівнянням
![]() ,
одержимо
,
одержимо
![]() або
або
![]() .
.
3) Нехай
маємо точку
![]() і
пряму, яку задано рівнянням з кутовим
коефіцієнтом
і
пряму, яку задано рівнянням з кутовим
коефіцієнтом
![]() .
.
Оскільки
![]() ,
то кутові коефіцієнти цих прямих
задовольняють рівність
,
то кутові коефіцієнти цих прямих
задовольняють рівність
![]() .
Враховуюче те, що
.
Враховуюче те, що
![]() ,
отримаємо
,
отримаємо
 .
Скориставшись рівнянням
.
Скориставшись рівнянням
![]() ,
маємо
,
маємо
 або
або
 .
.
Вправа
1.4. Знайти
координати точки
![]() перетину двох прямих.
перетину двох прямих.
1) Нехай
прямі задано загальними рівняннями
![]() і
і
![]() .
.
Розв’язання.
Прямі
перетинаються, тоді і тільки тоді, якщо
їх нормальні вектори не є паралельними.
В даному випадку
![]() і
і
 .
Отже,
.
Отже,
![]() .
Оскільки точка
.
Оскільки точка
![]() перетину
прямих належить і прямий
перетину
прямих належить і прямий
![]() і прямий
і прямий
![]() ,
то її координати задовольняють рівняння
обох прямих, тобто є розв’язком системи
рівнянь
,
то її координати задовольняють рівняння
обох прямих, тобто є розв’язком системи
рівнянь Розв’язавши систему, одержимо
Розв’язавши систему, одержимо
![]() і
і
![]() .
.
Отже,
прямі
![]() і
і
![]() перетинаються в точці
перетинаються в точці
![]() .
.
2) Пряма
![]() задана параметричними рівняннями, а
пряма
задана параметричними рівняннями, а
пряма
![]() - загальним.
- загальним.
Розв’язання.
Підставивши
координати поточної точки
![]() прямої
прямої
![]() в загальне рівняння прямої
в загальне рівняння прямої
![]() ,
з’ясуємо, при якому значенні параметра
,
з’ясуємо, при якому значенні параметра
![]() точка, що належить прямій
точка, що належить прямій
![]() ,
лежить також на прямій
,
лежить також на прямій
![]() .
Маємо
.
Маємо
![]() .
Звідки
.
Звідки
![]() .
Підставивши значення параметра
.
Підставивши значення параметра
![]() в рівняння прямої
в рівняння прямої
![]() ,
одержимо
,
одержимо
![]() .
.
Отже,
прямі
![]() і
і
![]() перетинаються в точці
перетинаються в точці
![]() .
.
Вправа
1.5. Знайти
кут
![]() між двома прямими.
між двома прямими.
1) Нехай
прямі задано загальними рівняннями
![]() .
.
Розв’язання.
Запишемо
нормальні вектори заданих прямих
![]() .За
формулою
.За
формулою![]() знайдемо
знайдемо
 .
.
Тоді
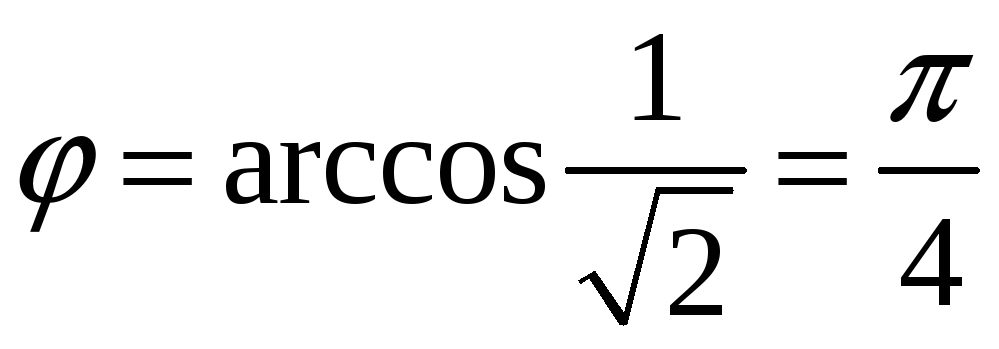 .
.
2) Нехай
прямі задано рівняннями з кутовими
коефіцієнтами
![]() .
.
Розв’язання.
Запишемо
кутові коефіцієнти заданих прямих
![]() .
За формулою
.
За формулою
![]() маємо
маємо
 .
Тоді
.
Тоді
![]() .
.
Вправа
1.6. Знайти
відстань від точки
![]() до прямої
до прямої
![]() .
.
Розв’язання.
За
формулою
![]() маємо
маємо
 .
Отже, відстань
.
Отже, відстань
![]() від точки
від точки
![]() до
прямої
до
прямої
![]() дорівнює
дорівнює
![]() .
.
Вправа
1.7. Знайти
площу трикутника, який відтинає від
координатного кута пряма
![]() .
.
Розв’язання.
Запишемо
для заданої прямої рівняння "у
відрізках"
![]()
 .
.
Як
бачимо, пряма відтинає від другого
координатного кута прямокутний трикутник
з катетами
![]() та
та
![]() .
Його площу обчислимо за формулою
.
Його площу обчислимо за формулою
 ,
тоді
,
тоді

Вправа
1.8. Знайти
1) проекцію точки
![]() на пряму, яка проходить через точки
на пряму, яка проходить через точки
![]() ,
2) точку, симетричну точці
,
2) точку, симетричну точці
![]() відносно цієї прямої.
відносно цієї прямої.
Розв’язання.
1 )
Запишемо рівняння прямої
)
Запишемо рівняння прямої
![]() .
Скориставшись рівнянням
.
Скориставшись рівнянням
![]() ,
одержимо
,
одержимо
 або
або
![]() .
.
Запишемо
тепер рівняння прямої
![]() ,
що проходить через точку
,
що проходить через точку
![]() перпендикулярно прямій
перпендикулярно прямій
![]() .
.
![]() .
За формулою
.
За формулою
![]() маємо
маємо
![]() або
або
![]() .
.
Знайдемо
проекцію точки
![]() на пряму
на пряму
![]() як точку перетину прямих
як точку перетину прямих
![]() та
та
![]() .
Позначимо її через
.
Позначимо її через
![]() (рис.7). Розв’язавши систему рівнянь
(рис.7). Розв’язавши систему рівнянь

одержимо
![]() .
.
2) Точку
![]() ,
симетричну точці
,
симетричну точці
![]() відносно
прямої
відносно
прямої
![]() ,знайдемо, враховуючи те, що
,знайдемо, враховуючи те, що
![]() є серединою відрізка
є серединою відрізка
![]() .
Отже її координати
.
Отже її координати
![]() дорівнюють середньому арифметичному
координат кінців відрізка. Тобто
дорівнюють середньому арифметичному
координат кінців відрізка. Тобто
 .
Тоді
.
Тоді
![]() .
.
Таким
чином,
![]() .
.
Вправа
1.9. Дано:
![]() .
.
-
Записати рівняння його сторін.
-
Записати рівняння висоти опущеної з вершини
 на сторону
на сторону
 .
Знайти довжину цієї висоти.
.
Знайти довжину цієї висоти. -
Записати рівняння медіани, проведеної з вершини
 на
сторону
на
сторону
 .
. -
Записати рівняння бісектриси внутрішнього кута при вершині
 .
.
Розв’язання.
1. Рівняння
сторін
![]() запишемо, скориставшись рівнянням
запишемо, скориставшись рівнянням
![]() ,
,
 або
або
![]() ;
;
 або
або
![]() ;
;
 або
або
![]() .
.
2. Опустимо
перпендикуляр
![]() з точки
з точки
![]() на сторону
на сторону
![]() .
.
![]() ,
,
![]() .
За формулою
.
За формулою
![]() одержимо
одержимо
![]() або
або
![]() .
.
Основу
цього перпендикуляра позначимо через
![]() .
Довжину висоти
.
Довжину висоти
![]() знайдемо як відстань від точки
знайдемо як відстань від точки
![]() до прямої
до прямої
![]() .
За формулою
.
За формулою
![]() маємо
маємо
 .
.
3. Нехай
![]() -
медіана, тоді точка
-
медіана, тоді точка
![]() -
середина відрізка
-
середина відрізка
![]() .
За формулами
.
За формулами
![]() одержимо
одержимо
 або
або
![]() .
Запишемо рівняння медіани
.
Запишемо рівняння медіани
![]() ,
скориставшись формулою
,
скориставшись формулою
![]() ,
,
 або
або
![]() .
.
4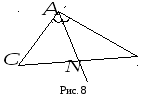 .
Відомо, що бісектриса внутрішнього кута
трикутника ділить протилежну сторону
на відрізки пропорційні прилеглим
сторонам. Отже, якщо точка
.
Відомо, що бісектриса внутрішнього кута
трикутника ділить протилежну сторону
на відрізки пропорційні прилеглим
сторонам. Отже, якщо точка
![]() -
точка перетину бісектриси зі стороною
-
точка перетину бісектриси зі стороною
![]() (рис.8), то
(рис.8), то
 .
.
Знайдемо
довжини сторін
![]() та
та
![]() .
.
![]() ,
,
![]() .
.
Тоді
 .
Отже,
.
Отже,
 .
Застосувавши формулу
.
Застосувавши формулу
![]() при
при
 ,
одержимо
,
одержимо
 або
або
 .
.
Користуючись
рівнянням
![]() ,
запишемо рівняння бісектриси
,
запишемо рівняння бісектриси
![]()
 або
або
![]() .
.
Вправа
1.10.
Записати рівняння прямої, яка проходить
через точку
![]() під кутом
під кутом
![]() до прямої
до прямої
![]() .
.
Розв’язання.
Як бачимо
на рисунку 9, існують 2 прямі
![]() і
і
![]() ,
що проходять через точку
,
що проходять через точку
![]() під
кутом
під
кутом
![]() до прямої
до прямої
![]() .
.
Я кщо
позначити через
кщо
позначити через
![]() - кутовий коефіцієнт прямої
- кутовий коефіцієнт прямої
![]() ,
то за формулою
,
то за формулою
![]() одержимо
одержимо
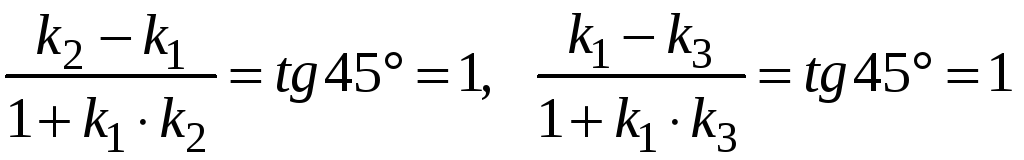 .
.
Запишемо
рівняння прямої
![]() з кутовим коефіцієнтом
з кутовим коефіцієнтом
 .
Тоді
.
Тоді
 .
З рівнянь
.
З рівнянь
 знаходимо:
знаходимо:
![]() і
і
![]() .
Застосувавши формулу
.
Застосувавши формулу
![]() маємо
маємо
![]() або
або
![]() ,
,
![]() або
або
![]() .
.
Вправа
1.11.
Задано
дві
вершини трикутника
![]() ,
,
![]() і точка перетину його висот
і точка перетину його висот
![]() .
Знайти координати третьої вершини
.
Знайти координати третьої вершини
![]() .
.
Розв’язання.
Оскільки
пряма
![]() - це висота, проведена до сторони
- це висота, проведена до сторони
![]() (рис.10), то
(рис.10), то
![]() ,
тобто
,
тобто
![]() - нормальний вектор прямої
- нормальний вектор прямої
![]() .
За формулою
.
За формулою
![]() одержимо
одержимо
![]() або
або
![]() .
.
Аналогічно
складаємо рівняння сторони
![]() за точкою
за точкою
![]() та нормальним вектором
та нормальним вектором
![]() .
.
![]() або
або
![]() .
.
Знайдемо
третю вершину
![]() як точку перетину прямих
як точку перетину прямих
![]() та
та
![]() .
.
 або
або
![]() .
Отже
.
Отже
![]() .
.

Вправи для самостійного розв’язування.
1.12.
Записати
рівняння прямої, яка проходить через
точку
![]() і точку перетину прямих
і точку перетину прямих
![]() та
та
![]()
1.13.
Записати
рівняння прямої, яка проходить через
точку
![]()
а)
паралельно прямій
![]() :
б) перпендикулярно прямій
:
б) перпендикулярно прямій
![]() .
.
1.14. Знайти кут між прямими
а)![]() ;
б)
;
б)
![]() ;
;
в) ;
г)
;
г)
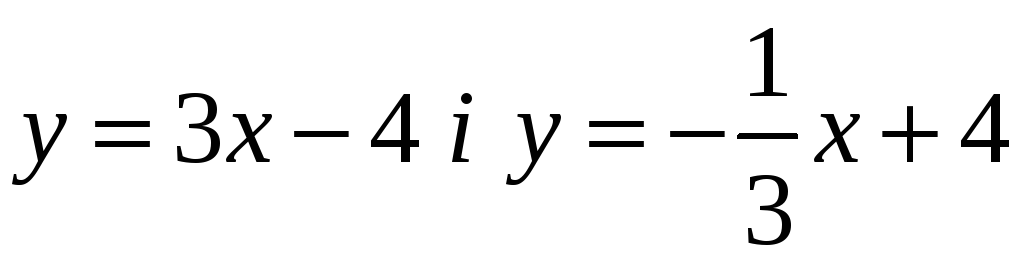 .
.
1.15.
Знайти
відстань між двома паралельними прямими
![]() та
та
![]() .
.
1.16.
Задано
рівняння двох сторін паралелограма
![]() та
та
![]() і точка перетину його діагоналей
і точка перетину його діагоналей
![]() .
Записати рівняння двох інших сторін.
.
Записати рівняння двох інших сторін.
1.17.
Задано
рівняння двох висот трикутника
![]() та координати однієї з його вершин
та координати однієї з його вершин
![]() .
Записати рівняння сторін цього трикутника.
.
Записати рівняння сторін цього трикутника.
1.18.
Задано
дві вершини трикутника
![]() і
і
![]() ,
рівняння сторони
,
рівняння сторони
![]() та медіани
та медіани
![]() .
Записати рівняння висоти, опущеної з
вершини
.
Записати рівняння висоти, опущеної з
вершини
![]() на сторону
на сторону
![]() та обчислити її довжину.
та обчислити її довжину.
1.19.
Між
пунктами
![]() і
і
![]() проходить шосейна дорога. На плані
місцевості ці пункти мають координати
проходить шосейна дорога. На плані
місцевості ці пункти мають координати
![]() (розміри в км).
Завод, що в цій же системі координат
позначено точкою
(розміри в км).
Завод, що в цій же системі координат
позначено точкою
![]() ,
треба з’єднати найкоротшим шляхом з
цим шосе. Знайти на шосе точку входження
в нього дороги і довжину дороги.
,
треба з’єднати найкоротшим шляхом з
цим шосе. Знайти на шосе точку входження
в нього дороги і довжину дороги.
