
- •Г.В. Соколовська с.Ю. Соколовський вища математика
- •Розділ 1. Інтегральне числення
- •§1. Первісна. Невизначений інтеграл та його властивості
- •Властивості невизначеного інтеграла
- •Основні формули інтегрування
- •§2. Метод заміни змінної (підстановки) у невизначеному інтегралі
- •§3. Інтегрування частинами у невизначеному інтегралі
- •§4. Інтегрування деяких виразів, що містять квадратний тричлен
- •§5. Інтегрування деяких ірраціональних і тригонометричних виразів
- •§6. Про функції, інтеграли від яких не виражаються через елементарні функції
- •§7. Визначений інтеграл та його властивості
- •Геометричний зміст визначеного інтеграла
- •Властивості визначеного інтеграла
- •§8. Інтеграл зі змінною верхньою межею
- •§9. Формула Ньютона - Лейбніца
- •§10. Заміна змінної у визначеному інтегралі
- •§11. Інтегрування частинами у визначеному інтегралі
- •§12. Невластиві інтеграли
- •1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
- •2. Інтеграли від розривної функції (невластиві інтеграли роду).
- •§12. Застосування визначеного інтеграла
- •1. Обчислення площі плоскої фігури.
- •2. Обчислення довжини дуги.
- •2. Обчислення об’єму за площею поперечного перерізу.
- •Розділ 2. Звичайні диференціальні рівняння
- •§1. Поняття про диференціальні рівняння
- •§2. Диференціальні рівняння першого порядку
- •§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
- •§4. Лінійні диференціальні рівняння другого порядку.
- •Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
- •Лінійні неоднорідні диференціальні рівняння.
- •Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
- •§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
- •Розділ 3. Ряди
- •§1. Властивості числового ряду.
- •Основні властивості рядів
- •§2. Ряди з додатними членами.
- •§3. Ряди з довільними членами.
- •§4. Ряди з чергуванням знаків.
- •§5. Функціональні ряди.
- •§6. Степеневий ряд.
- •§6. Розвинення функції в степеневий ряд.
§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
Розглянемо систему двох диференціальних рівнянь першого порядку
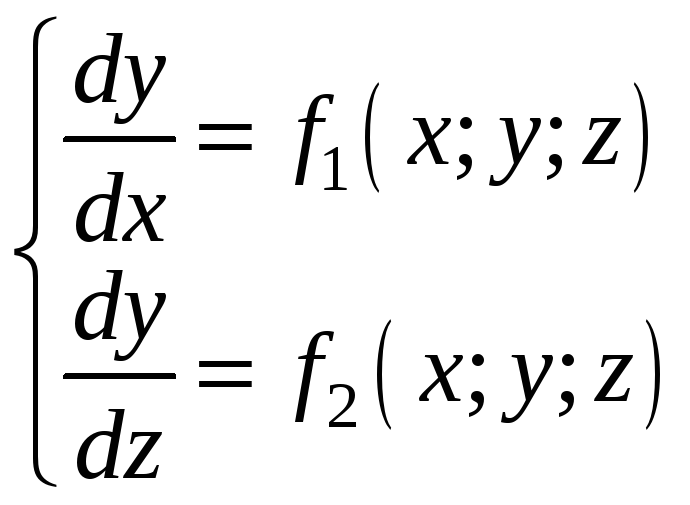
![]()
Розв’язок
системи (2.18) - пара функцій
![]() і
і
![]() ,
що задовольняє обидва рівняння.
,
що задовольняє обидва рівняння.
Задачею Коші назвемо сукупність системи (2.18) і початкових умов
![]()
![]()
Теорема
2.6
Нехай функції
![]() та їх частинні похідні по
та їх частинні похідні по
![]() і
і
![]() ,
неперервні в області
,
неперервні в області
![]() ,
що містить точку
,
що містить точку
![]() .
Тоді задача Коші (2.18), (2.19) має єдиний
розв’язок, визначений в деякому околі
точки
.
Тоді задача Коші (2.18), (2.19) має єдиний
розв’язок, визначений в деякому околі
точки
![]() .
.
Загальним
розв’язком системи називається
двопараметричне сімейство пар функцій
![]() ,
,
![]() ,
що задовольняє такі умови:
,
що задовольняє такі умови:
1) будь-яка пара функцій цього сімейства є розв’язком системи;
2) якими
б не були початкові умови (2.19) (точка
![]() належить області, де виконано умови
теореми 2.6), в цьому сімействі знайдеться
пара функцій, що їх задовольняє.
належить області, де виконано умови
теореми 2.6), в цьому сімействі знайдеться
пара функцій, що їх задовольняє.
Розглянемо систему диференціальних рівнянь зі сталими коефіцієнтами
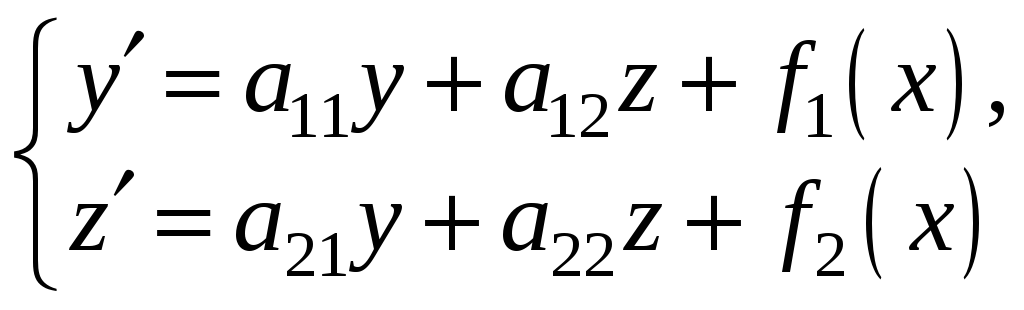 ,
,
![]()
де
![]() - деякі функції,
- деякі функції,
![]() .
Розв’язати таку систему можна звівши
її до одного лінійного рівняння другого
порядку. Покажемо на прикладі, як це
можна зробити.
.
Розв’язати таку систему можна звівши
її до одного лінійного рівняння другого
порядку. Покажемо на прикладі, як це
можна зробити.
Приклад.
Розв’язати задачу Коші
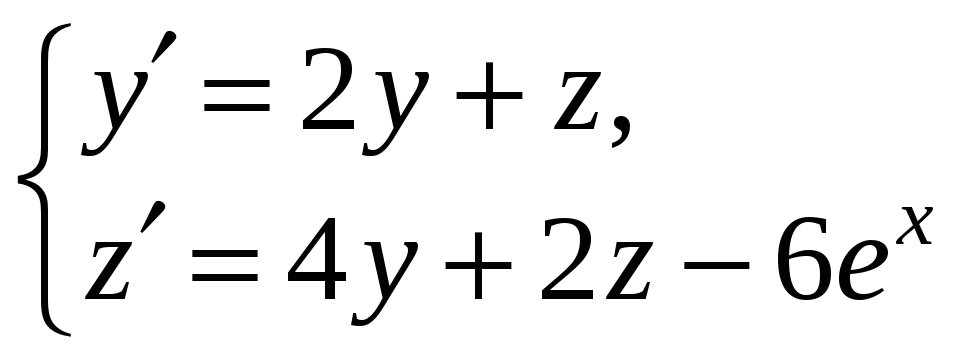 ,
,
![]() .
.
Розв’язання.
З першого рівняння знайдемо
![]() :
:
![]() .
Продиференціюємо по
.
Продиференціюємо по
![]() обидві частини цього рівняння . Маємо
обидві частини цього рівняння . Маємо
![]() .
Підставимо обидві ці рівності в друге
рівняння системи. Одержимо:
.
Підставимо обидві ці рівності в друге
рівняння системи. Одержимо:
![]() або
або
![]() .
.
Отримали
лінійне неоднорідне рівняння другого
порядку зі сталими коефіцієнтами, яке
було розглянуто у §4. Його розв’язок
має вигляд:
![]() (пропонуємо перевірити самостійно).
Одна з шуканих функцій
(пропонуємо перевірити самостійно).
Одна з шуканих функцій
![]() знайдена. Другу
знайдена. Другу
![]() знайдемо з рівняння
знайдемо з рівняння
![]() .
Оскілки
.
Оскілки
![]() ,
то
,
то
![]() ;
;
![]() .
.
Таким чином, загальний розв’язок системи:
![]() ;
;
![]() .
.
Підставивши
початкові умови, отримаємо:
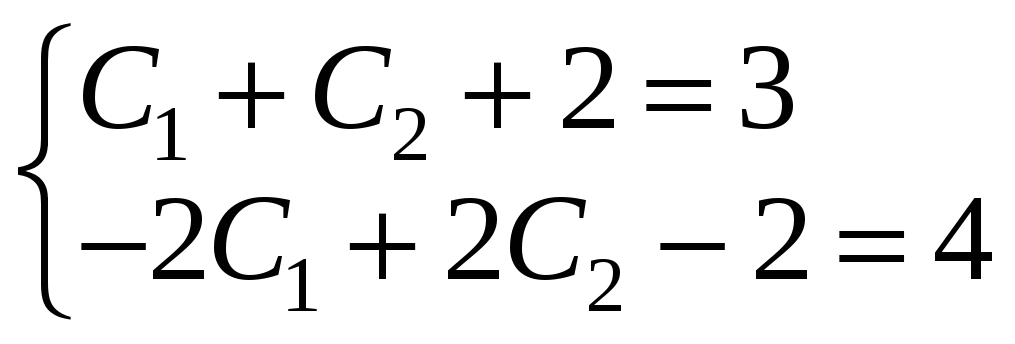 .
Розв’язавши цю систему, знайдемо:
.
Розв’язавши цю систему, знайдемо:
![]() .
Розв’язок задачі Коші
.
Розв’язок задачі Коші
![]() ,
,
![]() .
.
Розділ 3. Ряди
§1. Властивості числового ряду.
Означення.
Розглянемо
пронумеровану сукупність чисел
![]() .
Назвемо її числовою послідовністю.
Використовують
позначення:
.
Назвемо її числовою послідовністю.
Використовують
позначення:
![]()
![]() .
Числову послідовність доцільно задавати
формулою її загального члена, тобто
функцією
.
Числову послідовність доцільно задавати
формулою її загального члена, тобто
функцією
![]() від номера
від номера
![]() .
Наприклад, формулою загального члена
.
Наприклад, формулою загального члена
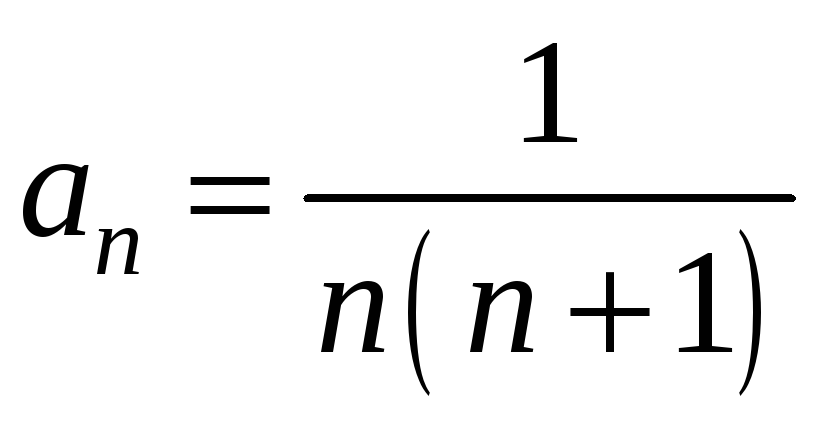 задається послідовність
задається послідовність
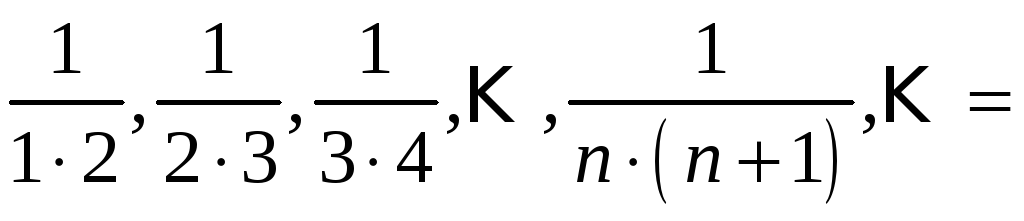
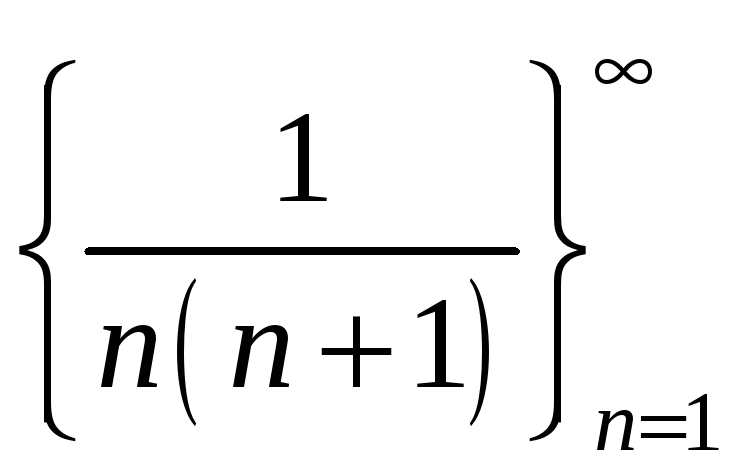 .
Числова послідовність називається
зростаючою, якщо
.
Числова послідовність називається
зростаючою, якщо
![]() ,
і спадною, якщо
,
і спадною, якщо![]() .
Якщо послідовність зростає або спадає,
то її називають монотонною. Кажуть, що
числова послідовність
.
Якщо послідовність зростає або спадає,
то її називають монотонною. Кажуть, що
числова послідовність
![]() , обмежена, якщо існує таке число
, обмежена, якщо існує таке число
![]() ,
що
,
що
![]() .
Число
.
Число
![]() називають границею числової послідовності
називають границею числової послідовності
![]() ,
якщо для будь-якого додатного числа
,
якщо для будь-якого додатного числа
![]() можна підібрати такий номер
можна підібрати такий номер
![]() ,
що
,
що
![]() .
Якщо послідовність має границю, то
кажуть, що вона збігається.
.
Якщо послідовність має границю, то
кажуть, що вона збігається.
Теорема 3.1 ( Вейерштраса) Монотонна і обмежена числова послідовність має границю.
Означення. Числовим рядом називається сума членів числової послідовності. Пишуть
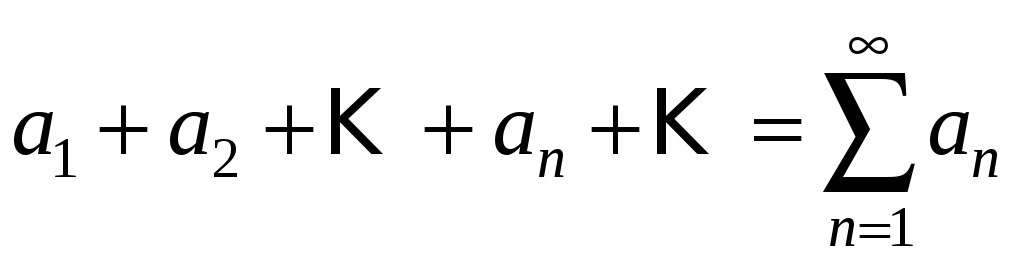 .
.
![]()
Числа
![]() називаються членами ряду,
називаються членами ряду,
![]() - його загальним членом.
- його загальним членом.
Суму
перших
![]() членів ряду назвемо його
членів ряду назвемо його
![]() -
ною частковою сумою. Введемо позначення
-
ною частковою сумою. Введемо позначення
![]() .
Надаючи
.
Надаючи
![]() значень
значень
![]() одержимо числову послідовність
одержимо числову послідовність
![]() - послідовність часткових сум ряду
(3.1). Кажуть, що ряд збігається, якщо
збігається послідовність його часткових
сум, тобто якщо існує скінченна границя
- послідовність часткових сум ряду
(3.1). Кажуть, що ряд збігається, якщо
збігається послідовність його часткових
сум, тобто якщо існує скінченна границя
![]() .
Число
.
Число
![]() називають сумою числового ряду (3.1),
тобто вважають, що
називають сумою числового ряду (3.1),
тобто вважають, що
![]() .
.
Приклади. Дослідити збіжність ряду.
1)
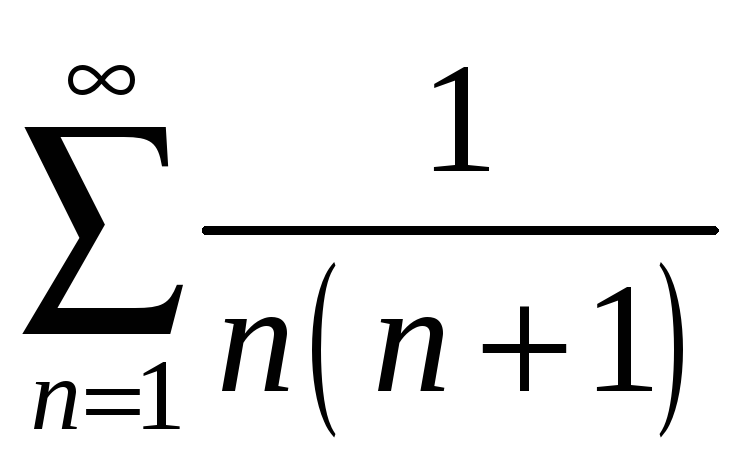 .
.
Розв’язання.
Запишемо
![]() - ну часткову суму
- ну часткову суму
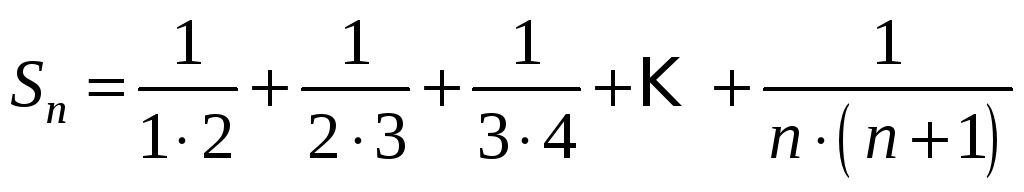 .
Зауважимо, що
.
Зауважимо, що
![]() ,
,
![]() .
Тоді
.
Тоді
![]() ;
;
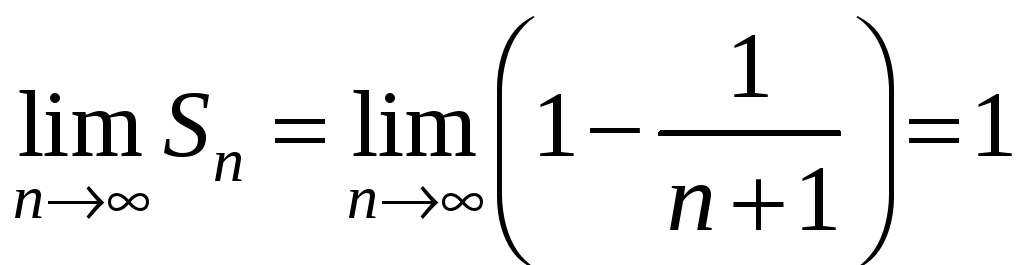 .
Отже, ряд збігається і його сума дорівнює
1.
.
Отже, ряд збігається і його сума дорівнює
1.
2)
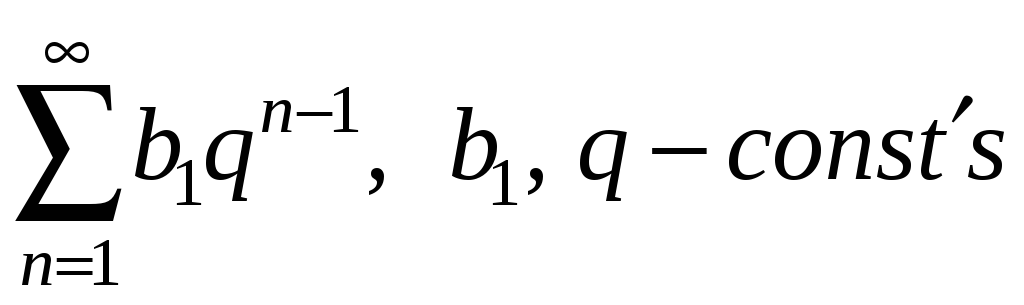 .
.
Розв’язання.
Такий ряд називається геометричним,
оскільки він є сумою членів геометричної
прогресії
![]() .
Скористаємося відомою формулою суми
перших
.
Скористаємося відомою формулою суми
перших
![]() членів геометричної прогресії:
членів геометричної прогресії:
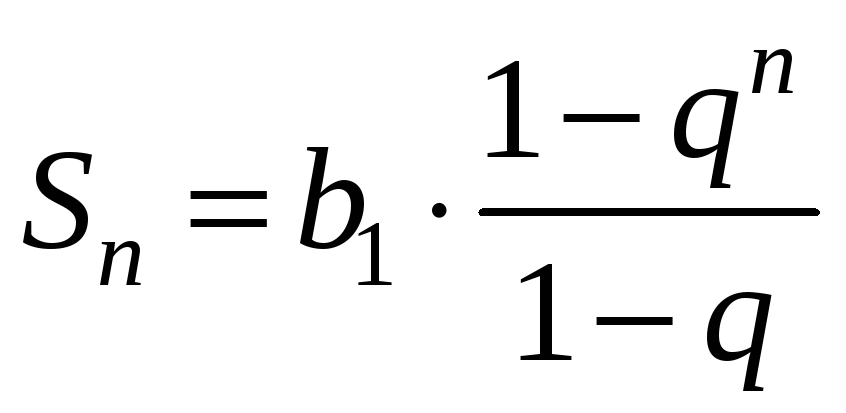 .
.
Нехай
![]() ,
тоді
,
тоді
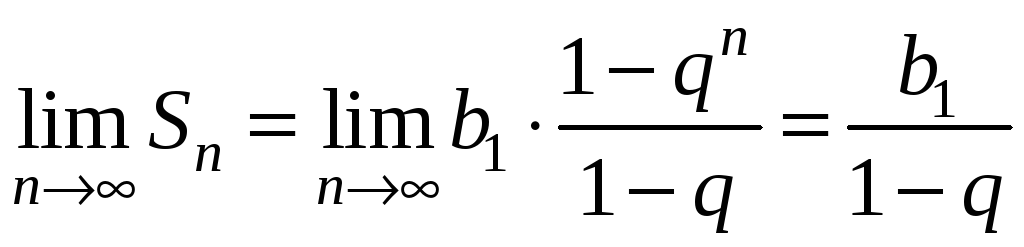 .
Отже, геометричний ряд збігається, якщо
.
Отже, геометричний ряд збігається, якщо
![]() ,
і його сума дорівнює
,
і його сума дорівнює
![]() .
.
Якщо
![]() ,
то
,
то
![]() .
Тоді
.
Тоді
![]() .
Якщо
.
Якщо
![]() ,
то
,
то
![]() не існує, оскільки не існує
не існує, оскільки не існує
![]() .
Таким чином, геометричний ряд розбігається
при
.
Таким чином, геометричний ряд розбігається
при
![]() .
.
Залишилось
розглянути тільки випадки
![]() .
Покажемо, що і в цих випадках ряд
розбігається. Якщо
.
Покажемо, що і в цих випадках ряд
розбігається. Якщо
![]() ,
то ряд має вигляд
,
то ряд має вигляд
![]() .
Тоді
.
Тоді
![]() ,
отже ряд розбігається. Якщо
,
отже ряд розбігається. Якщо
![]() ,
то ряд
,
то ряд
![]() також розбігається, оскільки послідовність
його часткових сум має вигляд
також розбігається, оскільки послідовність
його часткових сум має вигляд
![]() ,
тобто не має границі.
,
тобто не має границі.
