
- •Г.В. Соколовська с.Ю. Соколовський вища математика
- •Розділ 1. Інтегральне числення
- •§1. Первісна. Невизначений інтеграл та його властивості
- •Властивості невизначеного інтеграла
- •Основні формули інтегрування
- •§2. Метод заміни змінної (підстановки) у невизначеному інтегралі
- •§3. Інтегрування частинами у невизначеному інтегралі
- •§4. Інтегрування деяких виразів, що містять квадратний тричлен
- •§5. Інтегрування деяких ірраціональних і тригонометричних виразів
- •§6. Про функції, інтеграли від яких не виражаються через елементарні функції
- •§7. Визначений інтеграл та його властивості
- •Геометричний зміст визначеного інтеграла
- •Властивості визначеного інтеграла
- •§8. Інтеграл зі змінною верхньою межею
- •§9. Формула Ньютона - Лейбніца
- •§10. Заміна змінної у визначеному інтегралі
- •§11. Інтегрування частинами у визначеному інтегралі
- •§12. Невластиві інтеграли
- •1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
- •2. Інтеграли від розривної функції (невластиві інтеграли роду).
- •§12. Застосування визначеного інтеграла
- •1. Обчислення площі плоскої фігури.
- •2. Обчислення довжини дуги.
- •2. Обчислення об’єму за площею поперечного перерізу.
- •Розділ 2. Звичайні диференціальні рівняння
- •§1. Поняття про диференціальні рівняння
- •§2. Диференціальні рівняння першого порядку
- •§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
- •§4. Лінійні диференціальні рівняння другого порядку.
- •Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
- •Лінійні неоднорідні диференціальні рівняння.
- •Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
- •§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
- •Розділ 3. Ряди
- •§1. Властивості числового ряду.
- •Основні властивості рядів
- •§2. Ряди з додатними членами.
- •§3. Ряди з довільними членами.
- •§4. Ряди з чергуванням знаків.
- •§5. Функціональні ряди.
- •§6. Степеневий ряд.
- •§6. Розвинення функції в степеневий ряд.
Геометричний зміст визначеного інтеграла
З
геометричної точки зору
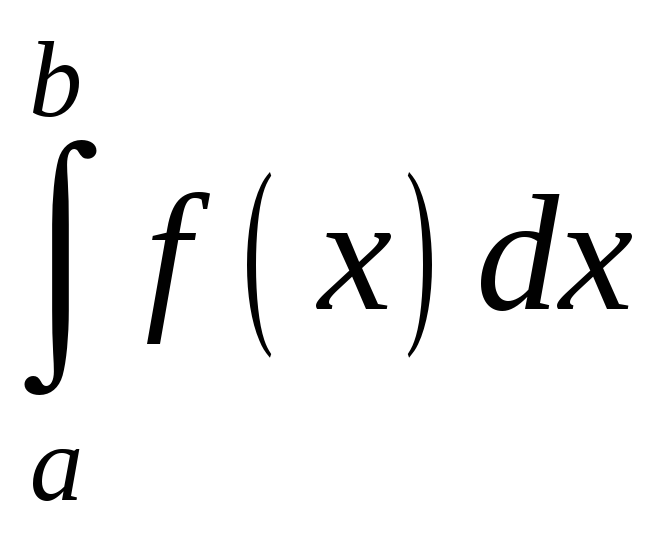 дорівнює площі криволінійної трапеції,
що обмежена лініями
дорівнює площі криволінійної трапеції,
що обмежена лініями
![]() та графіком неперервної й невід’ємної
на відрізку
та графіком неперервної й невід’ємної
на відрізку
![]() функції
функції
![]() .
.
Властивості визначеного інтеграла
1. Визначений інтеграл від суми двох або декількох функцій дорівнює сумі визначених інтегралів від цих функцій:
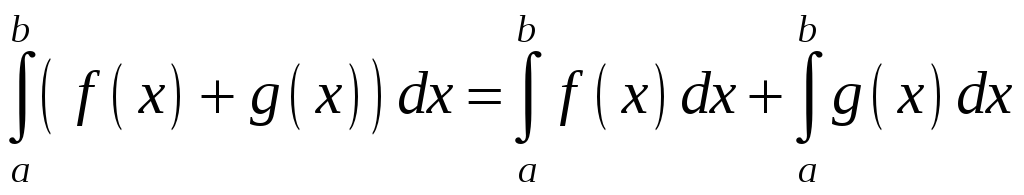 .
.
2. Сталий множник можна виносити за знак визначеного інтеграла:
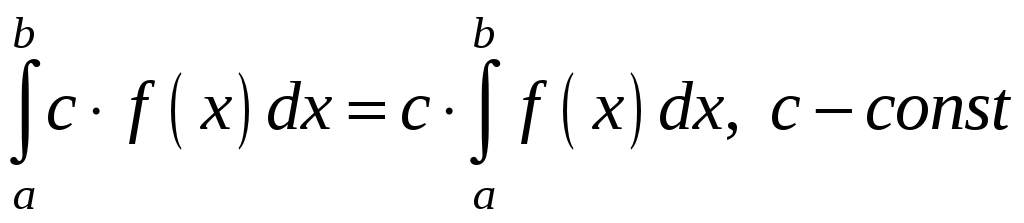 .
.
3. Якщо
проміжок інтегрування
![]() розбити точкою
розбити точкою
![]() на частини, то:
на частини, то:
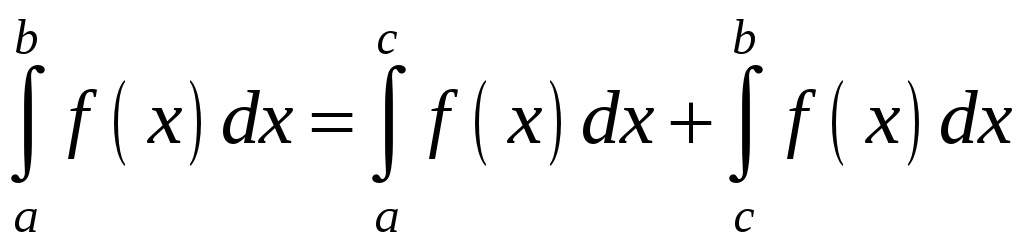 .
.
4. Нехай
на відрізку
![]() виконано нерівність
виконано нерівність
![]() ,
тоді
,
тоді
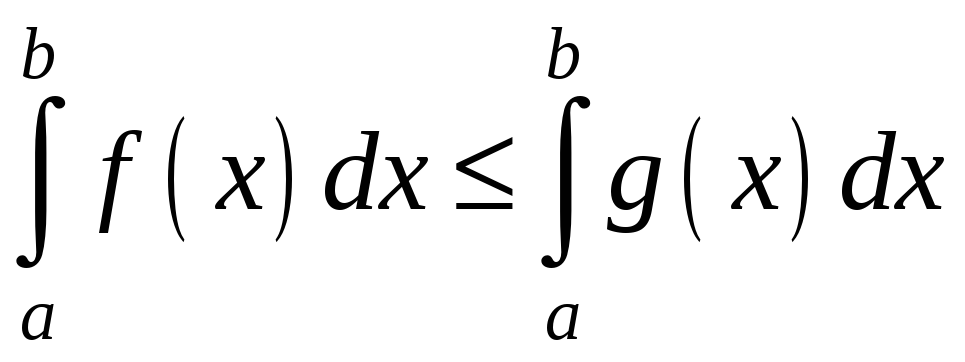 .
.
5.
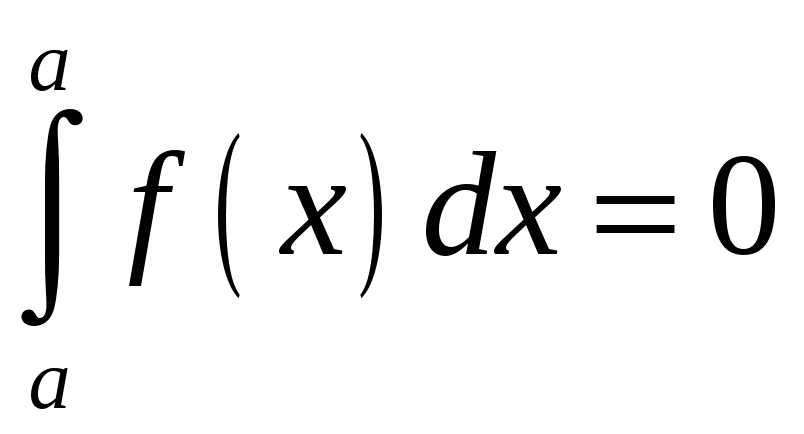 .
6.
.
6.
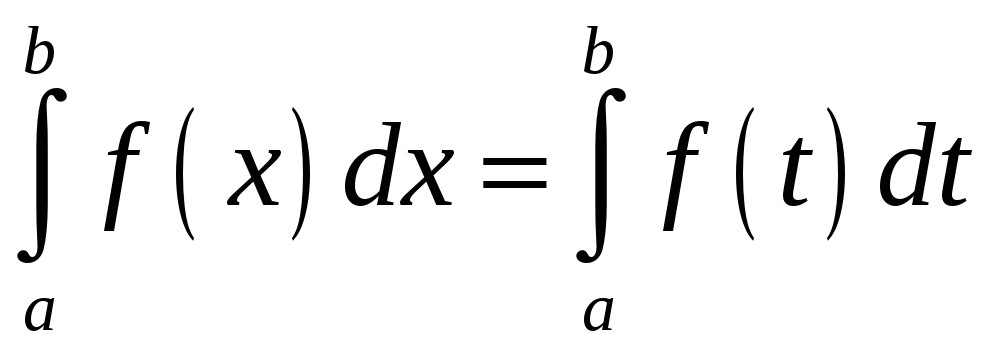 .
7.
.
7.
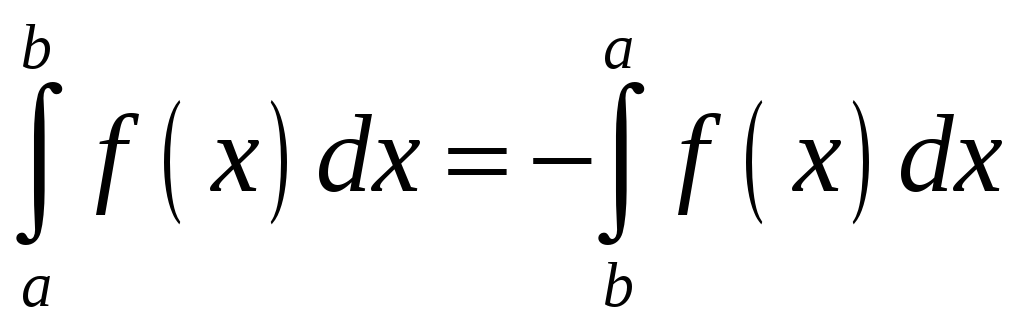
Справедливість
властивостей
![]() випливає або з самого означення
визначеного інтеграла як границі
інтегральної суми або з його геометричного
змісту.
випливає або з самого означення
визначеного інтеграла як границі
інтегральної суми або з його геометричного
змісту.
Теорема
1.5.
Нехай функція
![]() неперервна на відрізку
неперервна на відрізку
![]() ,
тоді на цьому відрізку знайдеться таке
число
,
тоді на цьому відрізку знайдеться таке
число
![]() ,
що
,
що
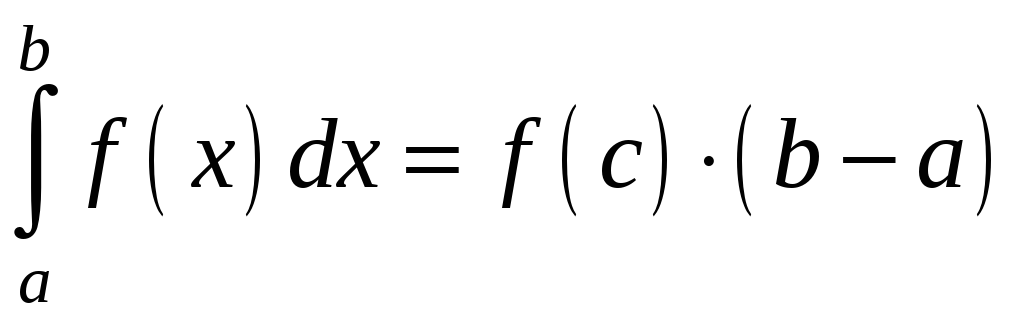
![]()
Доведення.
Якщо функція
![]() неперервна на відрізку
неперервна на відрізку![]() ,
то вона досягає на ньому свого найбільшого
,
то вона досягає на ньому свого найбільшого
![]() і найменшого
і найменшого
![]() значення.
значення.
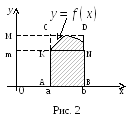
Тоді з геометричного змісту визначеного інтегралу випливає нерівність
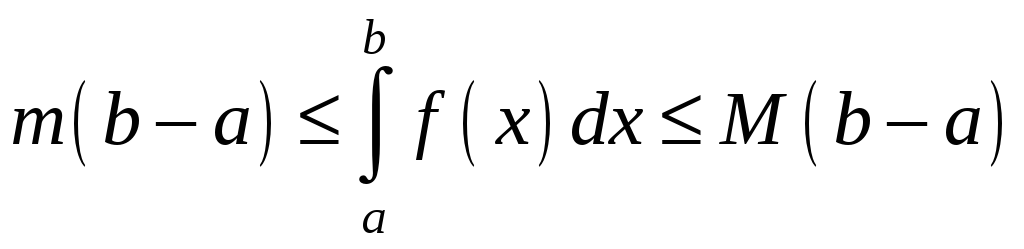 .
.
Адже
ліва і права частини цієї подвійної
нерівності відповідно дорівнюють площам
прямокутників
![]() та
та
![]() (рис.2), а середня частина – площі
криволінійної трапеції, що заштрихована.
Тоді, розділивши всі частини останньої
нерівності на
(рис.2), а середня частина – площі
криволінійної трапеції, що заштрихована.
Тоді, розділивши всі частини останньої
нерівності на
![]() ,
отримаємо:
,
отримаємо:
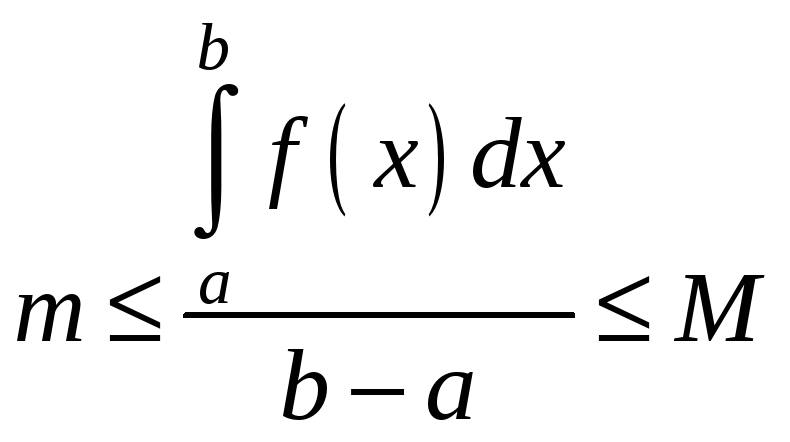 .
.
Позначимо
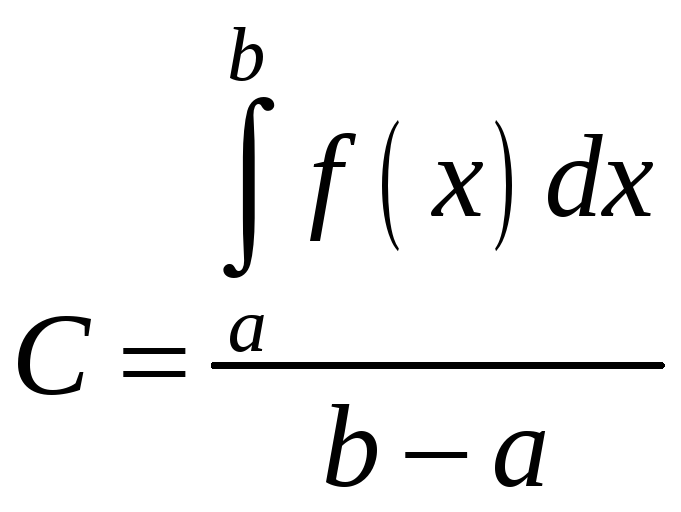 ,
тоді
,
тоді
![]() .
За теоремою про середнє значення
неперервної на відрізку
.
За теоремою про середнє значення
неперервної на відрізку
![]() функції
функції
![]() ,
існує така точка
,
існує така точка
![]() ,
в якій виконано
,
в якій виконано
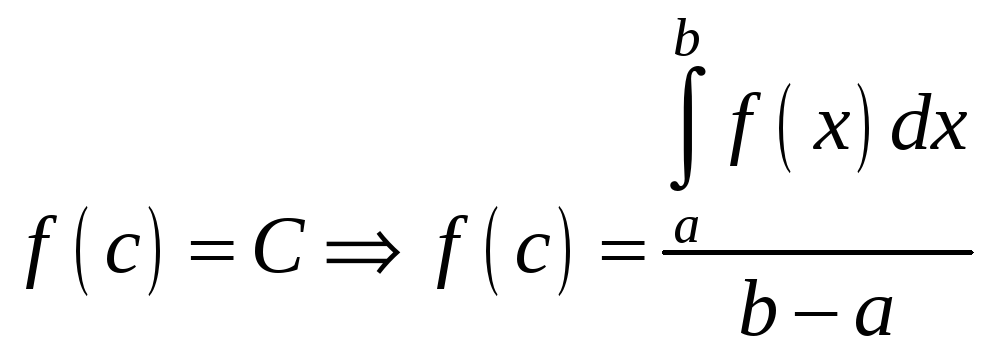 .
Помноживши обидві частин цієї рівності
на
.
Помноживши обидві частин цієї рівності
на
![]() одержимо рівність (1.7).
одержимо рівність (1.7).
§8. Інтеграл зі змінною верхньою межею
Якщо
функція
![]() неперервна на відрізку
неперервна на відрізку
![]() ,
то
,
то
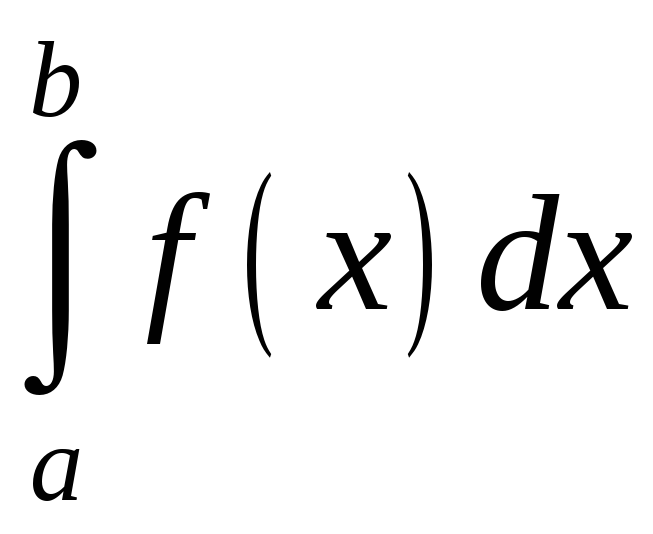 дорівнює певному числу. Якщо змінити
верхню межу
дорівнює певному числу. Якщо змінити
верхню межу
![]() так, щоб функція залишалася неперервною
на новому проміжку, то зміниться і
значення визначеного інтегралу. Таким
чином, визначений інтеграл можна
розглядати як функцію від верхньої межі
так, щоб функція залишалася неперервною
на новому проміжку, то зміниться і
значення визначеного інтегралу. Таким
чином, визначений інтеграл можна
розглядати як функцію від верхньої межі
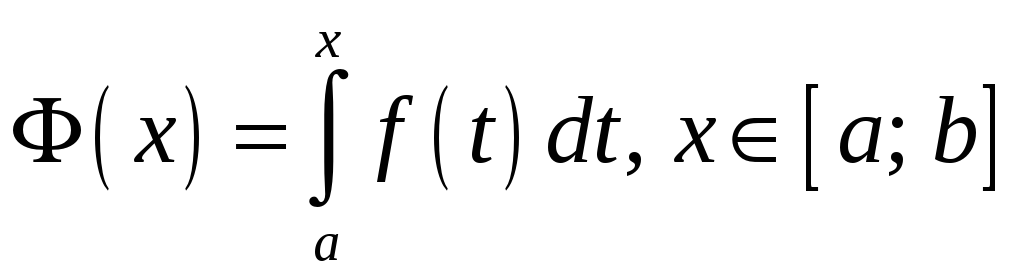 ,
,
![]() неперервна на
неперервна на
![]() .
.
Теорема
1.6
(Барроу
про похідну інтегралу зі змінною верхньою
межею).
Якщо функція
![]() неперервна на
неперервна на
![]() ,
то функція
,
то функція
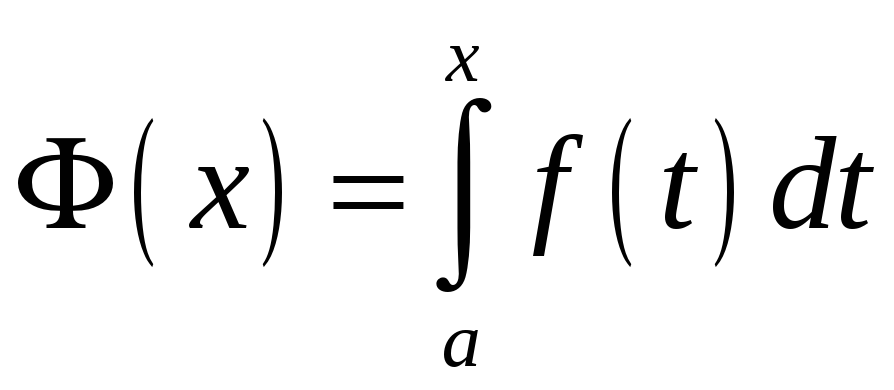 диференційовна на
диференційовна на
![]() по змінній
по змінній
![]() і
і
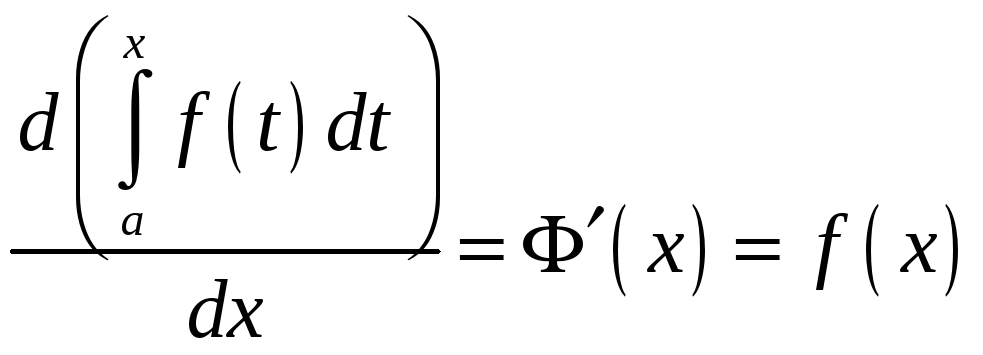
![]()
Доведення.
Зафіксуємо
![]() і обчислимо
і обчислимо
![]() .
З геометричної точки зору
.
З геометричної точки зору
![]() дорівнює площі криволінійної трапеції
(рис.3), побудованої на відрізку
дорівнює площі криволінійної трапеції
(рис.3), побудованої на відрізку
![]() .
Дамо аргументові
.
Дамо аргументові
![]() приріст
приріст
![]() і обчислимо
і обчислимо
![]() ,
що дорівнює площі криволінійної трапеції
з основою
,
що дорівнює площі криволінійної трапеції
з основою
![]() .
Приріст функції
.
Приріст функції
![]() тоді має вигляд:
тоді має вигляд:
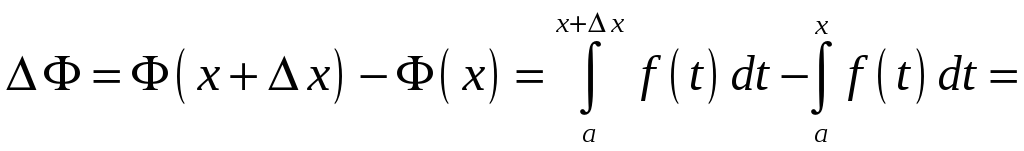
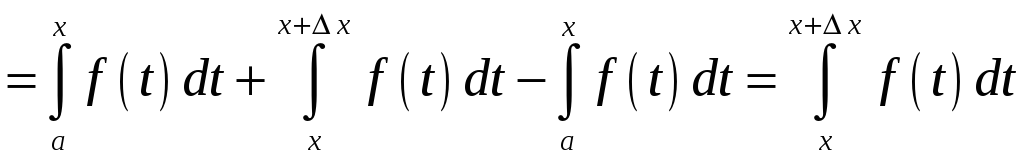 .
.
За
теоремою 1.5 маємо: існує така точка
![]() ,
що
,
що
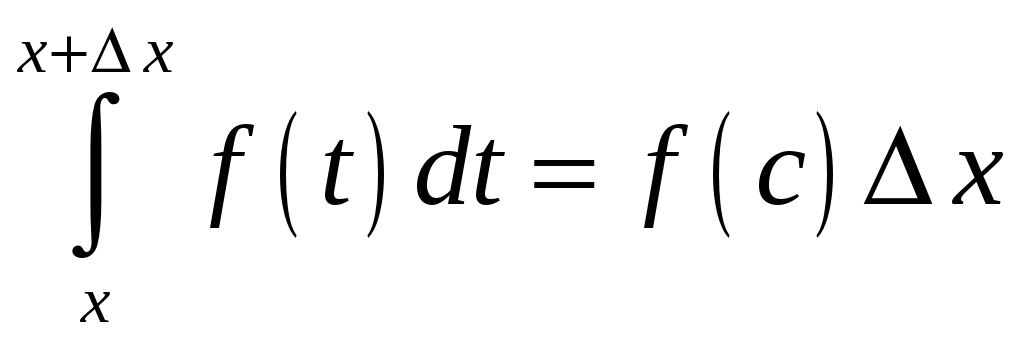 .
Знайдемо похідну функції
.
Знайдемо похідну функції
![]() за означенням.
за означенням.
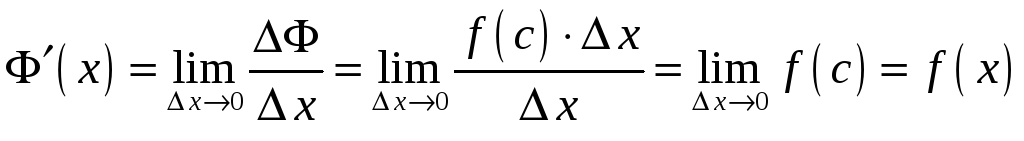 ,
тому, що
,
тому, що
![]() ,
коли
,
коли
![]() .
.
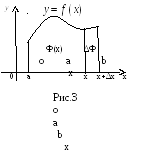
§9. Формула Ньютона - Лейбніца
Нехай
![]() - первісна для функції
- первісна для функції
![]() на
на
![]() .
За теоремою Барроу, інтеграл зі змінною
верхньою межею
.
За теоремою Барроу, інтеграл зі змінною
верхньою межею
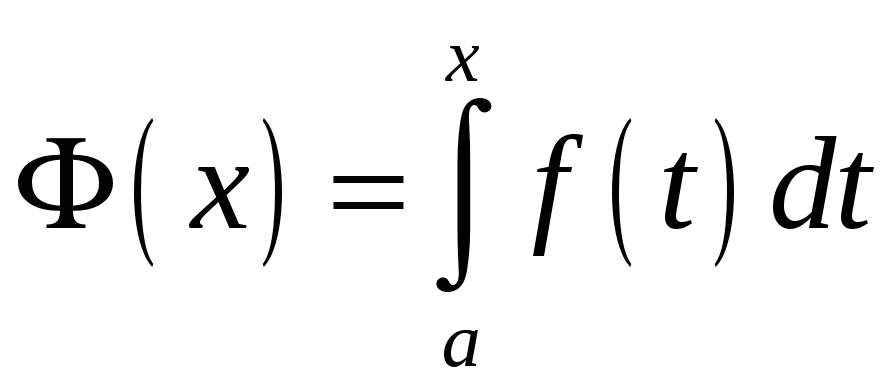 - також її первісна. Тоді
- також її первісна. Тоді
![]() і
і
![]() відрізняються одна від одної на сталий
доданок
відрізняються одна від одної на сталий
доданок
![]() .
Отже
.
Отже
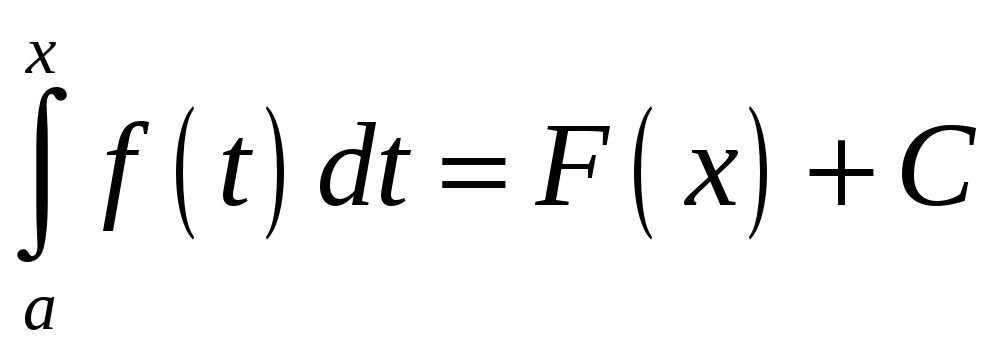
![]()
Підставимо
в обидві частини останньої рівності
![]() замість
замість
![]() .
Отримаємо:
.
Отримаємо:
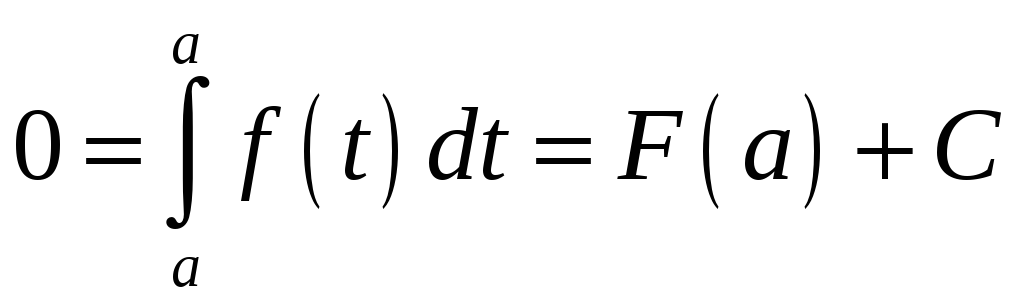 .
Звідки маємо:
.
Звідки маємо:
![]() .
Підставимо тепер в рівність (1.8)
.
Підставимо тепер в рівність (1.8)
![]() замість
замість
![]() і замінимо зміну інтегрування
і замінимо зміну інтегрування
![]() на
на
![]() ,
одержимо:
,
одержимо:
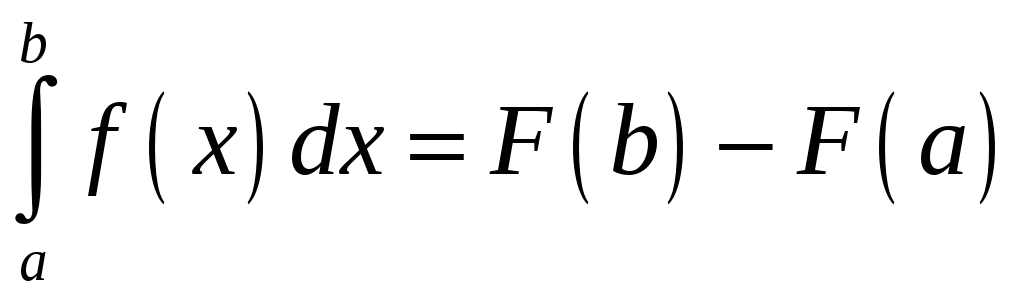
![]()
Формула
(1.9) називається формулою Ньютона –
Лейбніца. Якщо ввести позначення
![]() ,
то ця формула може бути записана так:
,
то ця формула може бути записана так:
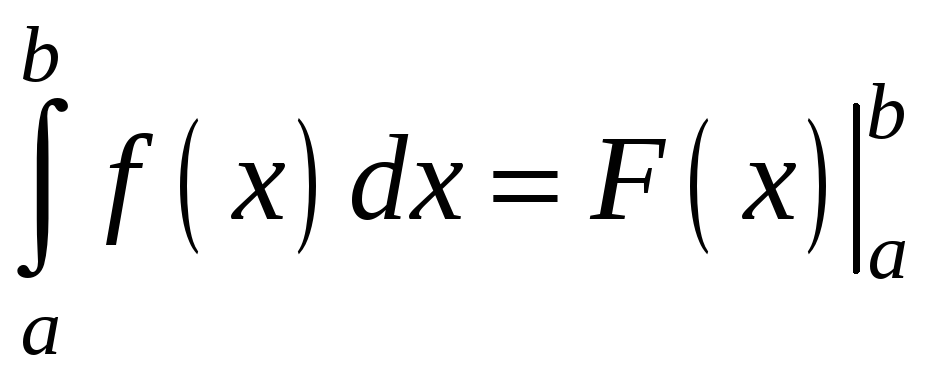 .
.
Приклад.
 .
.
