
- •Г.В. Соколовська с.Ю. Соколовський вища математика
- •Розділ 1. Інтегральне числення
- •§1. Первісна. Невизначений інтеграл та його властивості
- •Властивості невизначеного інтеграла
- •Основні формули інтегрування
- •§2. Метод заміни змінної (підстановки) у невизначеному інтегралі
- •§3. Інтегрування частинами у невизначеному інтегралі
- •§4. Інтегрування деяких виразів, що містять квадратний тричлен
- •§5. Інтегрування деяких ірраціональних і тригонометричних виразів
- •§6. Про функції, інтеграли від яких не виражаються через елементарні функції
- •§7. Визначений інтеграл та його властивості
- •Геометричний зміст визначеного інтеграла
- •Властивості визначеного інтеграла
- •§8. Інтеграл зі змінною верхньою межею
- •§9. Формула Ньютона - Лейбніца
- •§10. Заміна змінної у визначеному інтегралі
- •§11. Інтегрування частинами у визначеному інтегралі
- •§12. Невластиві інтеграли
- •1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
- •2. Інтеграли від розривної функції (невластиві інтеграли роду).
- •§12. Застосування визначеного інтеграла
- •1. Обчислення площі плоскої фігури.
- •2. Обчислення довжини дуги.
- •2. Обчислення об’єму за площею поперечного перерізу.
- •Розділ 2. Звичайні диференціальні рівняння
- •§1. Поняття про диференціальні рівняння
- •§2. Диференціальні рівняння першого порядку
- •§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
- •§4. Лінійні диференціальні рівняння другого порядку.
- •Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
- •Лінійні неоднорідні диференціальні рівняння.
- •Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
- •§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
- •Розділ 3. Ряди
- •§1. Властивості числового ряду.
- •Основні властивості рядів
- •§2. Ряди з додатними членами.
- •§3. Ряди з довільними членами.
- •§4. Ряди з чергуванням знаків.
- •§5. Функціональні ряди.
- •§6. Степеневий ряд.
- •§6. Розвинення функції в степеневий ряд.
Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
Розглянемо лінійне однорідне рівняння виду
![]() .
.
![]()
Його
називають рівнянням зі сталими
коефіцієнтами
![]() і
і
![]() .
Будемо шукати розв’язок рівняння (2.13)
у вигляді
.
Будемо шукати розв’язок рівняння (2.13)
у вигляді
![]() .
Тоді
.
Тоді
![]() .
Підставивши ці вирази у (2.13) маємо:
.
Підставивши ці вирази у (2.13) маємо:
![]() .
Оскільки
.
Оскільки![]() ,
то
,
то
![]() є розв’язком рівняння:
є розв’язком рівняння:
![]() .
.
![]()
Його називають характеристичним рівнянням. Розв’язавши квадратне рівняння (2.14) отримаємо три випадки.
1. Якщо
корені характеристичного рівняння
![]() і
і
![]() дійсні
і
дійсні
і
![]() ,
то частинні розв’язки рівняння (2.13)
,
то частинні розв’язки рівняння (2.13)
![]() і
і
![]() є
лінійно незалежними. Дійсно,
є
лінійно незалежними. Дійсно,
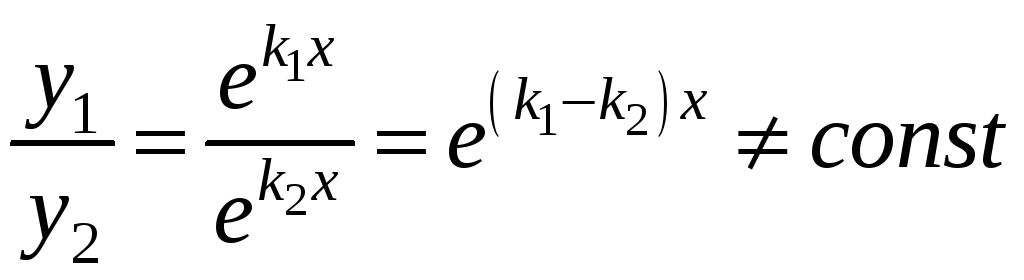 .
Тоді загальний розв’язок рівняння має
вигляд
.
Тоді загальний розв’язок рівняння має
вигляд
![]() ,
,
![]() і
і
![]() -
довільні сталі.
-
довільні сталі.
2. Нехай
корені характеристичного рівняння
![]() і
і
![]() дійсні і співпадають
дійсні і співпадають
![]() .
Тоді маємо частинний розв’язок
.
Тоді маємо частинний розв’язок
![]() .
Доведемо, що функція
.
Доведемо, що функція
![]() також
є частинним розв’язком рівняння (2.13).
Знайдемо похідні
також
є частинним розв’язком рівняння (2.13).
Знайдемо похідні
![]() ,
,
![]() і підставимо в рівняння. Маємо:
і підставимо в рівняння. Маємо:
![]() .
В останньому виразі перший доданок
дорівнює нулю через те, що
.
В останньому виразі перший доданок
дорівнює нулю через те, що
![]() -
корінь характеристичного рівняння.
Другий доданок також дорівнює нулю,
оскільки в цьому випадку дискримінант
рівняння (2.14)
-
корінь характеристичного рівняння.
Другий доданок також дорівнює нулю,
оскільки в цьому випадку дискримінант
рівняння (2.14)
![]() і
і
![]() .
Отже, маємо два розв’язки рівняння
(2.13)
.
Отже, маємо два розв’язки рівняння
(2.13)
![]() і
і
![]() .
При цьому
.
При цьому
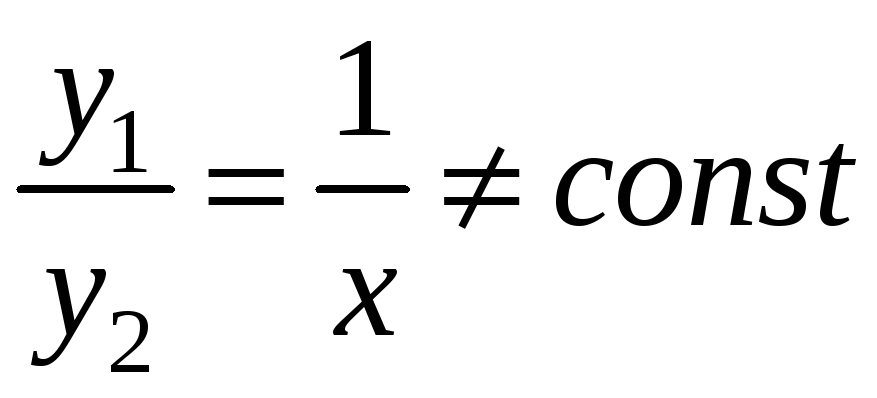 ,
тобто вони лінійно незалежні. Тоді
загальний розв’язок рівняння має вигляд
,
тобто вони лінійно незалежні. Тоді
загальний розв’язок рівняння має вигляд
![]() ,
,
![]() і
і
![]() -
довільні сталі.
-
довільні сталі.
3. Якщо
дискримінант характеристичного рівняння
від’ємний, тобто його корені комплексні
![]() ,
,
![]() ,
то лінійно незалежними розв’язками
рівняння (2.13) є
,
то лінійно незалежними розв’язками
рівняння (2.13) є
![]() і
і
![]() .
Пропонуємо студентам самостійно в цьому
переконатися, враховуючи, що
.
Пропонуємо студентам самостійно в цьому
переконатися, враховуючи, що
![]() ,
,
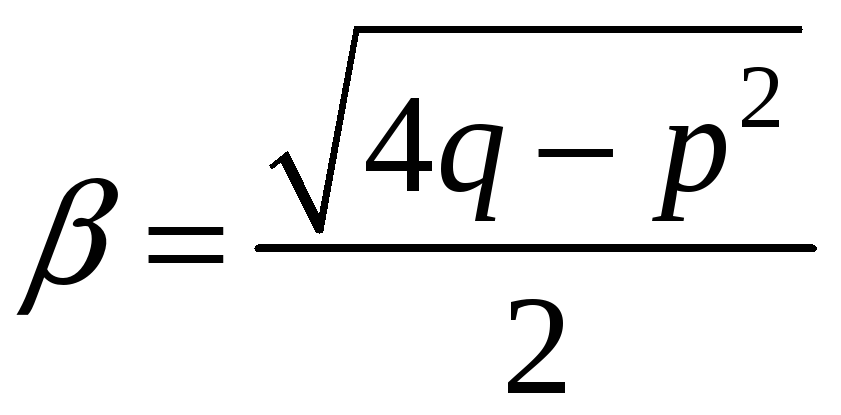 .
Отже, загальний розв’язок рівняння
(2.13) запишемо у вигляді
.
Отже, загальний розв’язок рівняння
(2.13) запишемо у вигляді
![]() ,
,
![]() і
і
![]() -
довільні сталі.
-
довільні сталі.
Приклади.
1)![]() .
.
Розв’язання.
Запишемо характеристичне рівняння
![]() .
Його корені дійсні і різні
.
Його корені дійсні і різні
![]() ,
,
![]() .
Загальний розв’язок рівняння:
.
Загальний розв’язок рівняння:
![]() .
.
2)
![]() .
.
Розв’язання.
Характеристичне рівняння
![]() має нульовий дискримінант. Його корені
співпадають
має нульовий дискримінант. Його корені
співпадають![]() .
Загальний розв’язок диференціального
рівняння:
.
Загальний розв’язок диференціального
рівняння:
![]() .
.
3)
![]() .
.
Розв’язання.
Характеристичне
рівняння
![]() має від’ємний дискримінант
має від’ємний дискримінант
![]() ,
,
![]() .
Знайдемо комплексні корені
.
Знайдемо комплексні корені
![]() ,
,
![]() .
Тобто
.
Тобто
![]() .
Загальний розв’язок диференціального
рівняння має вигляд:
.
Загальний розв’язок диференціального
рівняння має вигляд:
![]() .
.
Лінійні неоднорідні диференціальні рівняння.
Розглянемо лінійне неоднорідне рівняння виду
![]() .
.
![]()
Теорема
2.4
(про загальний розв’язок лінійного
неоднорідного диференціального
рівняння). Загальний розв’язок рівняння
(2.15) має вигляд
![]() ,
де
,
де
![]() -
загальний розв’язок лінійного однорідного
рівняння
-
загальний розв’язок лінійного однорідного
рівняння
![]() ,
,
![]() -
будь-який частинний розв’язок самого
рівняння (2.15).
-
будь-який частинний розв’язок самого
рівняння (2.15).
Теорема
2.5
(принцип суперпозиції розв’язків).Якщо
![]() - частинний розв’язок рівняння
- частинний розв’язок рівняння
![]() ,
,
![]() - частинний розв’язок рівняння
- частинний розв’язок рівняння
![]() ,
то функція
,
то функція
![]() є частинним розв’язком рівняння
є частинним розв’язком рівняння
![]() .
.
Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
1. Розглянемо лінійне неоднорідне рівняння виду
![]()
![]()
де
![]() ,
,
![]() -
многочлен степеня
-
многочлен степеня
![]() .
Його загальний розв’язок знайдемо за
теоремою 2.4. Загальний розв’язок
.
Його загальний розв’язок знайдемо за
теоремою 2.4. Загальний розв’язок
![]() рівняння
рівняння
![]() ми вже вміємо знаходити. Можна довести,
що існує частинний розв’язок рівняння
(2.16), який має вигляд
ми вже вміємо знаходити. Можна довести,
що існує частинний розв’язок рівняння
(2.16), який має вигляд
![]() .
Тут
.
Тут
![]() -
многочлен того ж степеня, що і в правій
частині рівняння,
-
многочлен того ж степеня, що і в правій
частині рівняння,
![]() -
кількість коренів характеристичного
рівняння
-
кількість коренів характеристичного
рівняння
![]() ,
які співпадають з числом
,
які співпадають з числом
![]() .
Отже
.
Отже
![]() ,
якщо
,
якщо
![]() ;
;
![]() ,
якщо один з коренів характеристичного
рівняння дорівнює
,
якщо один з коренів характеристичного
рівняння дорівнює![]() ;
;
![]() ,
якщо
,
якщо
![]() .
.
Приклади.
1)
![]() .
.
Розв’язання.
Шукаємо загальний розв’язок у вигляді
![]() .
Для знаходження
.
Для знаходження
![]() ,
загального розв’язку рівняння
,
загального розв’язку рівняння
![]() ,
розв’яжемо характеристичне рівняння
,
розв’яжемо характеристичне рівняння
![]() .
Маємо:
.
Маємо:
![]() .
Тоді
.
Тоді
![]() .
Зауважимо, що права частина лінійного
неоднорідного рівняння має вигляд
.
Зауважимо, що права частина лінійного
неоднорідного рівняння має вигляд
![]() де
де
![]() ,
,
![]() -
многочлен нульового степеня
-
многочлен нульового степеня
![]() .
Тому його частинний розв’язок слід
шукати у вигляді
.
Тому його частинний розв’язок слід
шукати у вигляді
![]() ,
де
,
де
![]() -
поки що невизначений коефіцієнт. Знайдемо
-
поки що невизначений коефіцієнт. Знайдемо
![]() підставивши
підставивши
![]() в
лінійне неоднорідне рівняння. Оскільки
в
лінійне неоднорідне рівняння. Оскільки
![]() ,
то
,
то
![]() .
Звідки маємо:
.
Звідки маємо:
![]() .
Тоді
.
Тоді
![]() ,
загальний розв’язок:
,
загальний розв’язок:
![]() .
.
2)
![]() .
.
Розв’язання.
Спочатку розв’яжемо лінійне однорідне
рівняння
![]() за допомогою характеристичного рівняння
за допомогою характеристичного рівняння
![]() .
Його корені
.
Його корені
![]() ,
,
![]() .
Тому
.
Тому
![]() .
Праву частину лінійного неоднорідного
рівняння можна розглядати як добуток
многочлена першого степеня
.
Праву частину лінійного неоднорідного
рівняння можна розглядати як добуток
многочлена першого степеня
![]() і
і
![]() ( тобто
( тобто
![]() ).
Тому частинний розв’язок
).
Тому частинний розв’язок
![]() слід шукати у вигляді
слід шукати у вигляді
![]() або
або
![]() .
Тоді
.
Тоді
![]() .
Підставивши ці вирази в рівняння маємо:
.
Підставивши ці вирази в рівняння маємо:
![]() або
або
![]() .
.
Прирівняємо
коефіцієнти при однакових степенях
![]() в лівій і правій частинах останньої
рівності.
в лівій і правій частинах останньої
рівності.
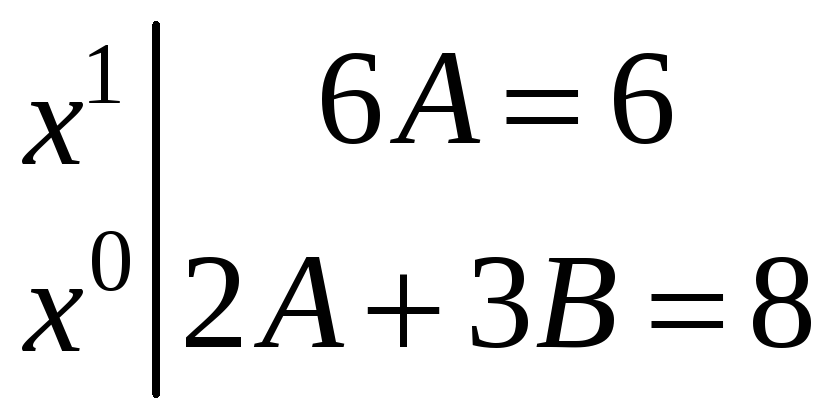 .
Розв’язавши отриману систему лінійних
алгебраїчних рівнянь, одержимо
.
Розв’язавши отриману систему лінійних
алгебраїчних рівнянь, одержимо
![]() .Тоді
.Тоді
![]() ,
загальний розв’язок рівняння має
вигляд:
,
загальний розв’язок рівняння має
вигляд:
![]() .
.
3)
![]() .
.
Розв’язання.
Знайдемо
![]() -
загальний розв’язок лінійного
однорідного рівняння
-
загальний розв’язок лінійного
однорідного рівняння
![]() .
Запишемо його характеристичне рівняння
.
Запишемо його характеристичне рівняння
![]() .
Його корені співпадають
.
Його корені співпадають
![]() .
Тому
.
Тому
![]() .
Частинний розв’язок лінійного
неоднорідного рівняння шукаємо у вигляді
.
Частинний розв’язок лінійного
неоднорідного рівняння шукаємо у вигляді
![]() (оскільки обидва корені характеристичного
рівняння співпадають з
(оскільки обидва корені характеристичного
рівняння співпадають з
![]() ,
тобто
,
тобто
![]() ).
Знайдемо
).
Знайдемо
![]() ,
,
![]() .
Підставивши ці вирази в лінійне
неоднорідне рівняння маємо:
.
Підставивши ці вирази в лінійне
неоднорідне рівняння маємо:
![]() або
або
![]() .
Звідки
.
Звідки
![]() .
Таким чином,
.
Таким чином,
![]() .
Загальний розв’язок рівняння:
.
Загальний розв’язок рівняння:
![]() .
.
2. Нехай лінійне неоднорідне рівняння має вигляд
![]() ,
,
![]()
![]() .
Можна довести, що існує частинний
розв’язок рівняння (2.17) виду
.
Можна довести, що існує частинний
розв’язок рівняння (2.17) виду
![]() .
Тут
.
Тут
![]() ,
,
![]() - кількість коренів характеристичного
рівняння, які співпадають з комплексним
числом
- кількість коренів характеристичного
рівняння, які співпадають з комплексним
числом
![]() .
.
Приклад.
![]() .
.
Розв’язання.
Знайдемо загальний розв’язок рівняння
![]() .
Його характеристичне рівняння
.
Його характеристичне рівняння
![]() ;
;
![]() .
Тоді
.
Тоді
![]() .
Частинний розв’язок лінійного
неоднорідного рівняння шукаємо у вигляді
.
Частинний розв’язок лінійного
неоднорідного рівняння шукаємо у вигляді
![]() .
Тоді
.
Тоді
![]() ,
,
![]() .
Підставимо ці вирази в рівняння і
прирівняємо коефіцієнти в лівій і правій
частині при
.
Підставимо ці вирази в рівняння і
прирівняємо коефіцієнти в лівій і правій
частині при
![]() і
і
![]() .
Маємо:
.
Маємо:
![]()
![]() ;
;
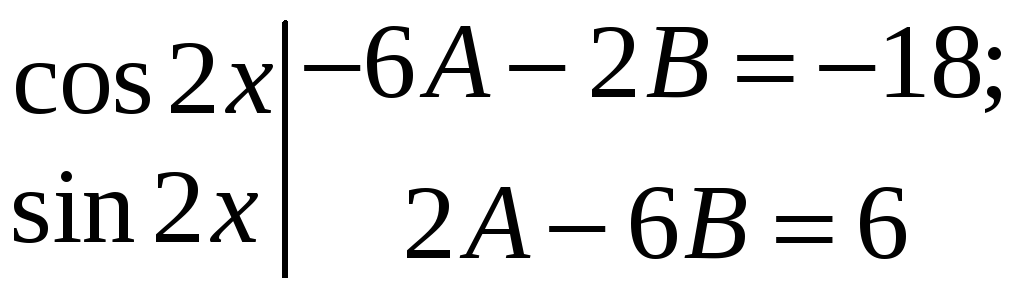 .
Розв’язавши систему одержимо
.
Розв’язавши систему одержимо
![]() ,
,
![]() .
Отже
.
Отже
![]() .
Тоді загальний розв’язок рівняння має
вигляд:
.
Тоді загальний розв’язок рівняння має
вигляд:
![]() .
.
3. Нехай лінійне неоднорідне рівняння має вигляд
![]() -
многочлени степенів
-
многочлени степенів
![]() та
та
![]() відповідно. Частинний розв’язок такого
рівняння слід шукати у вигляді
відповідно. Частинний розв’язок такого
рівняння слід шукати у вигляді
![]() ,
де
,
де
![]() ;
;
![]() - многочлени степенів
- многочлени степенів
![]() ,
,
![]() - кількість коренів характеристичного
рівняння, які співпадають з комплексним
числом
- кількість коренів характеристичного
рівняння, які співпадають з комплексним
числом
![]() .
Рівняння, розглянуті в пунктах 1 і 2,
також є рівняннями цього вигляду. Дійсно,
у випадку 1 маємо:
.
Рівняння, розглянуті в пунктах 1 і 2,
також є рівняннями цього вигляду. Дійсно,
у випадку 1 маємо:
![]() ,
у випадку 2:
,
у випадку 2:
![]() .
.
Зауваження.
Нехай права частина лінійного неоднорідного
рівняння є сумою декількох функцій,
розглянутих у пункті 3. Тоді для знаходження
частинного розв’язку можна скористатися
принципом суперпозиції розв’язків.
Наприклад, частинний розв’язок рівняння
![]() слід шукати у вигляді
слід шукати у вигляді
![]() ,
де
,
де
![]() -
невизначені коефіцієнти. Якщо права
частина рівняння не відповідає жодному
з розглянутих видів, то для його
розв’язання можна скористатися методом
варіації сталих. З цим методом пропонуємо,
ознайомитися самостійно (дивитися
-
невизначені коефіцієнти. Якщо права
частина рівняння не відповідає жодному
з розглянутих видів, то для його
розв’язання можна скористатися методом
варіації сталих. З цим методом пропонуємо,
ознайомитися самостійно (дивитися
![]() ,
,
![]() ).
).
