
- •Г.В. Соколовська с.Ю. Соколовський вища математика
- •Розділ 1. Інтегральне числення
- •§1. Первісна. Невизначений інтеграл та його властивості
- •Властивості невизначеного інтеграла
- •Основні формули інтегрування
- •§2. Метод заміни змінної (підстановки) у невизначеному інтегралі
- •§3. Інтегрування частинами у невизначеному інтегралі
- •§4. Інтегрування деяких виразів, що містять квадратний тричлен
- •§5. Інтегрування деяких ірраціональних і тригонометричних виразів
- •§6. Про функції, інтеграли від яких не виражаються через елементарні функції
- •§7. Визначений інтеграл та його властивості
- •Геометричний зміст визначеного інтеграла
- •Властивості визначеного інтеграла
- •§8. Інтеграл зі змінною верхньою межею
- •§9. Формула Ньютона - Лейбніца
- •§10. Заміна змінної у визначеному інтегралі
- •§11. Інтегрування частинами у визначеному інтегралі
- •§12. Невластиві інтеграли
- •1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
- •2. Інтеграли від розривної функції (невластиві інтеграли роду).
- •§12. Застосування визначеного інтеграла
- •1. Обчислення площі плоскої фігури.
- •2. Обчислення довжини дуги.
- •2. Обчислення об’єму за площею поперечного перерізу.
- •Розділ 2. Звичайні диференціальні рівняння
- •§1. Поняття про диференціальні рівняння
- •§2. Диференціальні рівняння першого порядку
- •§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
- •§4. Лінійні диференціальні рівняння другого порядку.
- •Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
- •Лінійні неоднорідні диференціальні рівняння.
- •Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
- •§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
- •Розділ 3. Ряди
- •§1. Властивості числового ряду.
- •Основні властивості рядів
- •§2. Ряди з додатними членами.
- •§3. Ряди з довільними членами.
- •§4. Ряди з чергуванням знаків.
- •§5. Функціональні ряди.
- •§6. Степеневий ряд.
- •§6. Розвинення функції в степеневий ряд.
§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
Означення. Диференціальне рівняння другого порядку, розв’язане відносно старшої похідної, має вигляд:
![]() .
.
![]()
Якщо до диференціального рівняння (2.10) приєднані початкові умови
![]() ,
,
![]()
то кажуть , що задано задачу Коші (2.10), (2.11).
Теорема
2.2 Якщо
функція
![]() і її частинні похідні по
і її частинні похідні по
![]() та по
та по
![]() неперервні у деякій області
неперервні у деякій області
![]() ,
що містить точку
,
що містить точку
![]() ,
то існує єдиний розв’язок задачі Коші
(2.10), (2.11), визначений у деякому околі
точки
,
то існує єдиний розв’язок задачі Коші
(2.10), (2.11), визначений у деякому околі
точки
![]() .
.
Означення.
Загальним
розв’язком диференціального рівняння
другого порядку називається двопараметричне
сімейство функцій
![]() ,
що має такі властивості:
,
що має такі властивості:
1) будь-яка функція цього сімейства є розв’язком рівняння (2.10);
2) для
будь-яких початкових умов (2.11) (точка
![]() належить області, в якій виконано умови
теореми 2.2), можна так підібрати
належить області, в якій виконано умови
теореми 2.2), можна так підібрати
![]() і
і
![]() ,
що функція
,
що функція
![]() буде їх задовольняти.
буде їх задовольняти.
Якщо
надати сталим
![]() і
і
![]() конкретних
значень, то отримаємо частинний розв’язок.
Розглянемо декілька видів рівнянь
(2.10) які зводяться до рівнянь першого
порядку, тобто допускають зниження
порядку.
конкретних
значень, то отримаємо частинний розв’язок.
Розглянемо декілька видів рівнянь
(2.10) які зводяться до рівнянь першого
порядку, тобто допускають зниження
порядку.
1. Нехай
рівняння має вигляд
![]() .
Його можна розв’язати проінтегрувавши
двічі обидві його частини.
.
Його можна розв’язати проінтегрувавши
двічі обидві його частини.
Приклад.
![]() .
.
Розв’язання.
![]() .
Тоді
.
Тоді
![]() .
.
2.
Розглянемо рівняння
![]() ,
яке не містить невідомої функції
,
яке не містить невідомої функції
![]() в явному вигляді, тоді роль невідомої
функції може виконати її похідна
в явному вигляді, тоді роль невідомої
функції може виконати її похідна
![]() .
За допомогою заміни
.
За допомогою заміни
![]() таке рівняння зводиться до рівняння
першого порядку
таке рівняння зводиться до рівняння
першого порядку
![]() .
Розв’язавши його знайдемо
.
Розв’язавши його знайдемо
![]() ,
а потім з рівняння
,
а потім з рівняння
![]() знайдемо
знайдемо
![]() .
.
Приклад.
![]() .
.
Розв’язання.
Застосуємо заміну
![]() .
Отримаємо рівняння першого порядку
.
Отримаємо рівняння першого порядку
![]() ,
яке є однорідним. Виконаємо у ньому
заміну
,
яке є однорідним. Виконаємо у ньому
заміну
![]() .
Одержимо
.
Одержимо
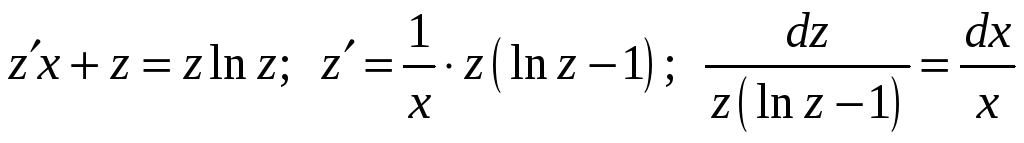 ;
;
![]() .
Замінивши
.
Замінивши
![]() на
на
![]() отримаємо
отримаємо
![]() .
Застосувавши метод інтегрування
частинами, одержимо загальний розв’язок
.
Застосувавши метод інтегрування
частинами, одержимо загальний розв’язок
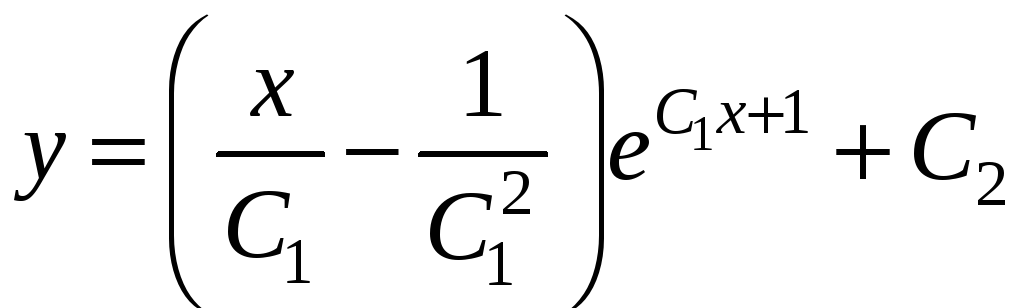 .
.
3.
Розглянемо рівняння
![]() ,
яке не містить незалежної змінної.
Знизити порядок такого рівняння можна
за допомогою заміни
,
яке не містить незалежної змінної.
Знизити порядок такого рівняння можна
за допомогою заміни
![]() (
(![]() вважаємо незалежною змінною). Тоді
вважаємо незалежною змінною). Тоді
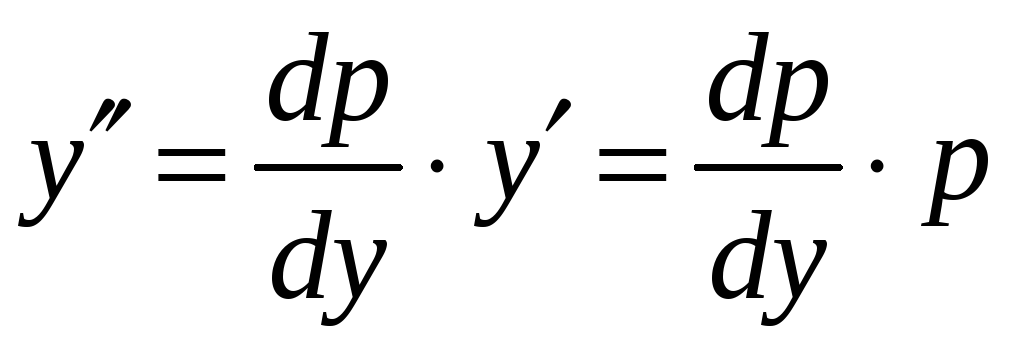 і рівняння набуває вигляду
і рівняння набуває вигляду
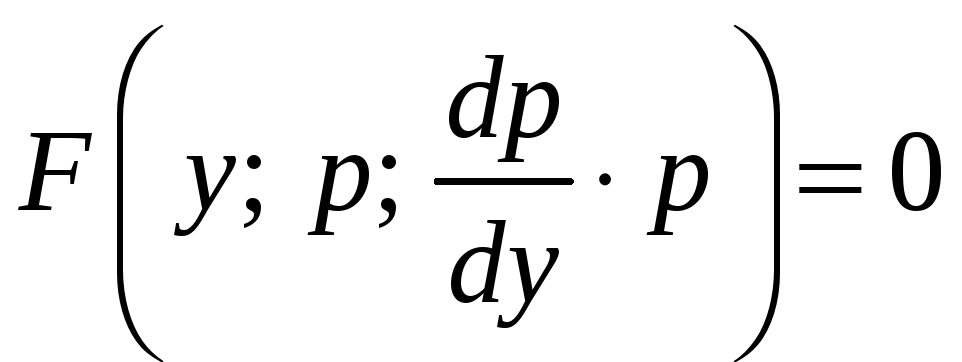 .
Нехай
.
Нехай
![]() -
загальний розв’язок цього рівняння,
тоді
-
загальний розв’язок цього рівняння,
тоді
![]() .
Останнє рівняння є рівнянням з
відокремлюваними змінними. Розв’язавши
його, отримаємо шукану функцію
.
Останнє рівняння є рівнянням з
відокремлюваними змінними. Розв’язавши
його, отримаємо шукану функцію
![]() .
.
Приклад.
Розв’язати задачу Коші
![]() .
.
Розв’язання.
Рівняння не містить
![]() ,
тому виконаємо заміну
,
тому виконаємо заміну
![]() ,
,
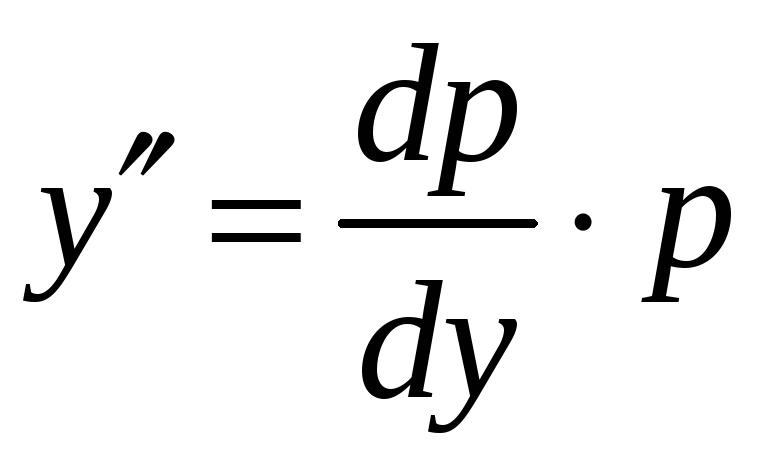 .
Отримаємо рівняння першого порядку з
відокремлюваними змінними
.
Отримаємо рівняння першого порядку з
відокремлюваними змінними
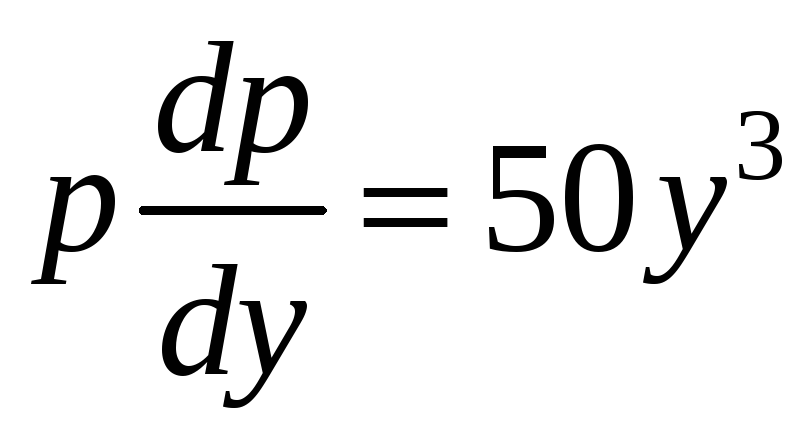 .
Тоді
.
Тоді
![]() ;
;
![]() .
В останню рівність підставимо обидві
початкові умови (обравши перед квадратним
коренем знак «+», щоб вони виконувались),
одержимо:
.
В останню рівність підставимо обидві
початкові умови (обравши перед квадратним
коренем знак «+», щоб вони виконувались),
одержимо:
![]() ,
звідки
,
звідки
![]() .
Тоді
.
Тоді
![]() або
або
![]() .
Розв’яжемо останнє рівняння:
.
Розв’яжемо останнє рівняння:
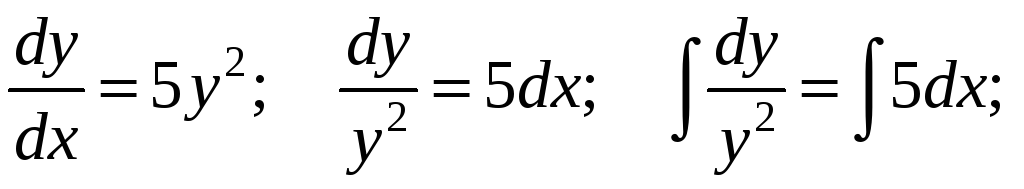
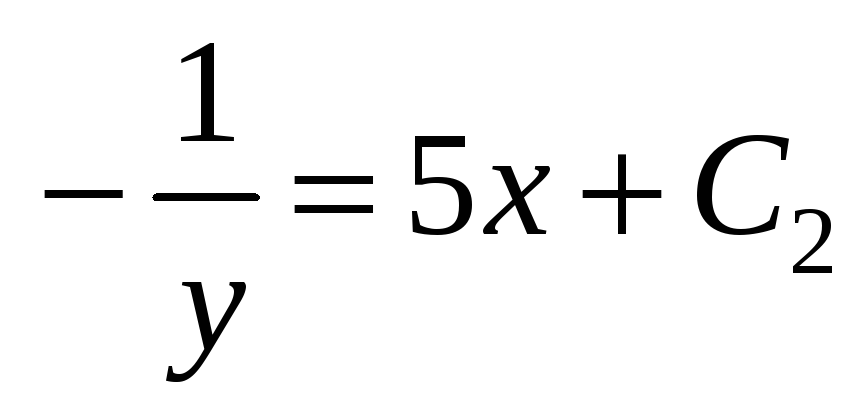 ;
;
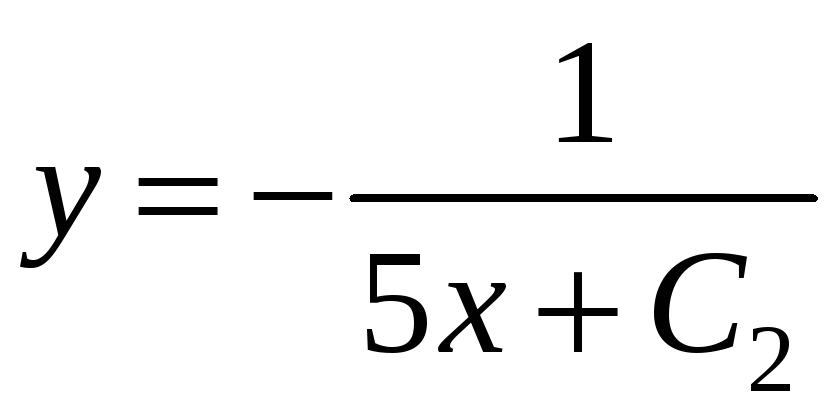 .
З початкової умови
.
З початкової умови
![]() ,
маємо:
,
маємо:
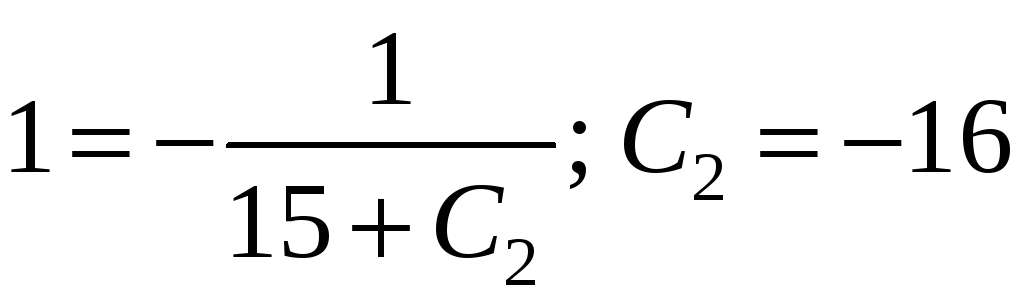 .
Отримали загальний розв’язок
.
Отримали загальний розв’язок
![]() .
.
§4. Лінійні диференціальні рівняння другого порядку.
Означення.
Лінійним
диференціальним рівнянням другого
порядку називається рівняння виду
![]() ,
де
,
де
![]() - задані функції. Якщо
- задані функції. Якщо
![]() ,
то рівняння називається лінійним
однорідним, у протилежному випадку -
лінійним неоднорідним.
,
то рівняння називається лінійним
однорідним, у протилежному випадку -
лінійним неоднорідним.
Лінійні однорідні рівняння.
Розглянемо основні властивості розв’язків лінійних однорідних диференціальних рівнянь
![]() .
.
![]()
1.
Диференціальне рівняння (2.12) має
тривіальний розв’язок
![]() .
.
2. Якщо
функції
![]() та
та
![]() - частинні розв’язки рівняння (2.12), то
їх лінійна комбінація
- частинні розв’язки рівняння (2.12), то
їх лінійна комбінація
![]() ,
також є розв’язком цього рівняння.
Дійсно,
,
також є розв’язком цього рівняння.
Дійсно,
![]()
![]()
![]() .
.
Отже,
лінійна комбінація
![]() також задовольняє рівняння (2.12).
також задовольняє рівняння (2.12).
Означення.
Функції
![]() і
і
![]() називаються лінійно незалежними, на
відрізку
називаються лінійно незалежними, на
відрізку
![]() ,
якщо функція
,
якщо функція
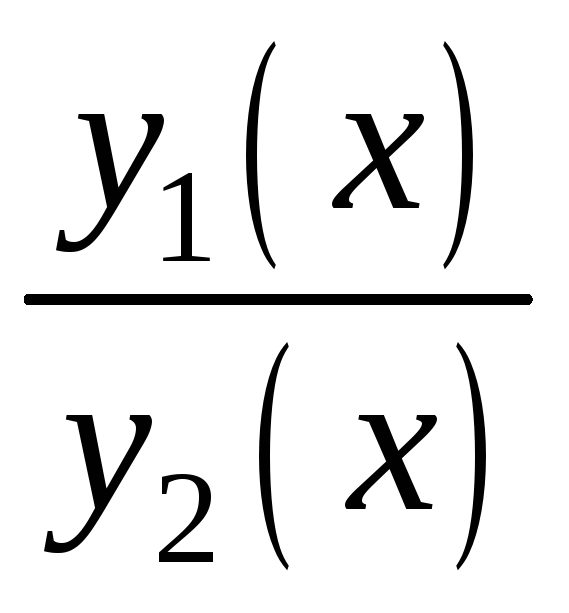 не є сталою на цьому відрізку.
не є сталою на цьому відрізку.
Теорема
2.3 (про
загальний розв’язок лінійного однорідного
диференціального рівняння). Якщо функції
![]() і
і
![]() - лінійно незалежні частинні розв’язки
рівняння (2.12), то його загальний розв’язок
має вигляд
- лінійно незалежні частинні розв’язки
рівняння (2.12), то його загальний розв’язок
має вигляд
![]() ,
де
,
де
![]() і
і
![]() - довільні сталі.
- довільні сталі.
Із
доведенням можна ознайомитись у
підручниках
![]() і
і
![]() .
.
