§2. Диференціальні рівняння першого порядку

Диференціальне рівняння першого порядку, має вигляд . Надалі будемо розглядати тільки рівняння, розв’язані відносно похідної невідомої функції, тобто такі диференціальні рівняння першого порядку, які можна записати у вигляді

.

Означення. Будь-яка функція , що задовольняє рівняння (2.3) називається його розв’язком. Графік цієї функції називають інтегральною кривою рівняння (2.3).

Приклад. Довести, що функція є розв’язком рівняння . Дійсно, .

Зауважимо, що будь-яка функція виду, , також є розв’язком цього рівняння. Тобто рівняння має безліч розв’язків.

Означення. Задачею Коші для диференціального рівняння першого порядку називається сукупність диференціального рівняння (2.3) і початкової умови

,

де - деякі числа.

Розв’язати задачу Коші означає знайти такий розв’язок рівняння (2.3), який задовольняє початкову умову (2.4), тобто знайти інтегральну криву рівняння, що проходить через точку .

Теорема 2.1 (достатня умова існування єдиного розв’язку задачі Коші). Якщо в деякій області , що містить початкову точку функція і її частинна похідна неперервні, то задача Коші (2.3), (2.4) має розв’язок, причому лише один, визначений в деякому околі точки .

Означення. Загальним розв’язком диференціального рівняння першого порядку називається однопараметричне сімейство функцій , що задовольняє такі умови:

1) будь-яка функція цього сімейства є розв’язком рівняння (2.3);

2) для будь-якої початкової умови (2.4) в цьому сімействі знайдеться функція, що її задовольняє ( початкова точка належить області, в якій виконано умови теореми 2.1).

Частинним розв’язком диференціального рівняння називається розв’язок, який отримаємо із загального при деякому конкретному значенні сталої .

Отже, загальний розв’язок рівняння (2.3) – це сімейство інтегральних кривих. Якщо в околі точки виконано умови теореми 2.1, то через цю точку проходить тільки одна інтегральна крива вказаного сімейства.

Наведемо методи розв’язування декількох типів диференціальних рівнянь першого порядку.

1. Рівняння з відокремлюваними змінними мають вигляд

.

Як бачимо, права частина цього рівняння є добутком функції лише від і функції тільки від . Це дає можливість "відокремити змінні", тобто за допомогою множення обох частин рівняння (2.5) на вираз 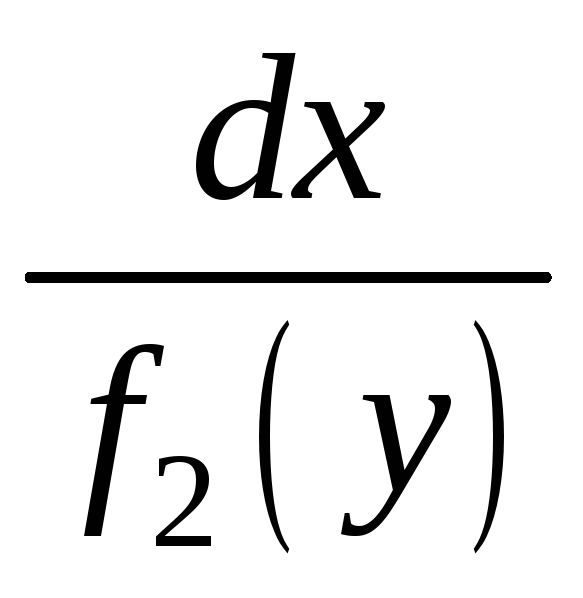перетворити його на таке рівняння:

.

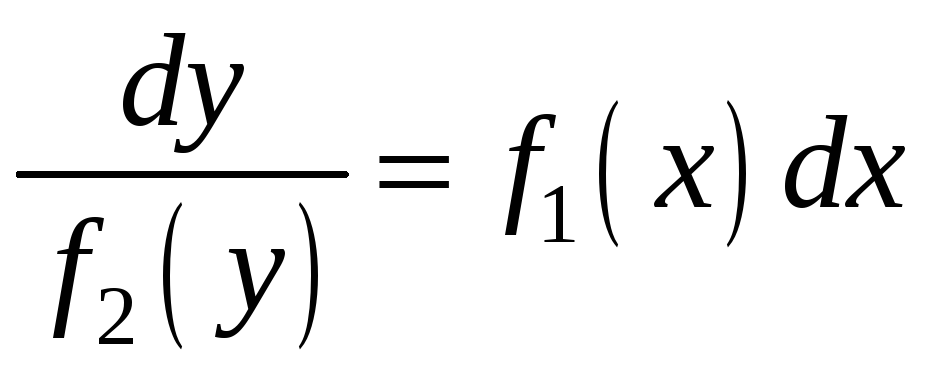Нехай нам відома функція , яка задовольняє рівняння (2.5), тоді в обох частинах рівняння (2.6) стоять диференціали, що є тотожно рівними. Якщо диференціали рівні, то невизначені інтеграли від них можуть відрізнятись лише на сталий доданок. Інтегруючи обидві частини (ліву по , праву по ), одержимо: 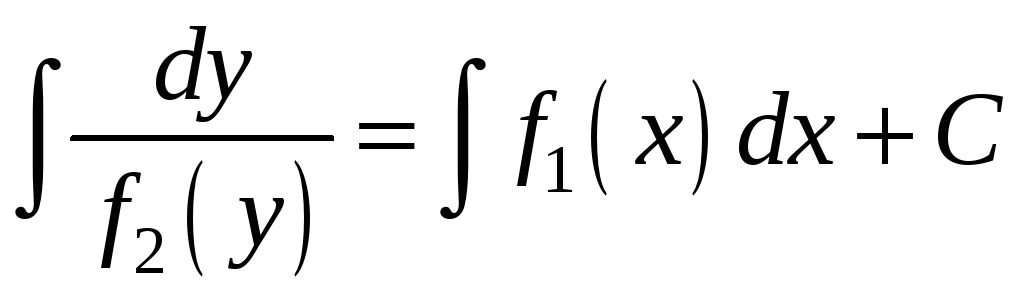. Ця рівність неявно задає загальний розв’язок . Її називають загальним інтегралом рівняння (2.6) . Зауважимо, що розділивши обидві частини рівності (2.5) на , ми виключили з розгляду ті значення , при яких . Нехай - таке число, що . Тоді функція також є розв’язком рівняння (2.5). Його називають особливим розв’язком.

Приклад. Розв’язати диференціальне рівняння .

Розв’язання. Запишемо рівняння у вигляді . Помножимо обидві частини на 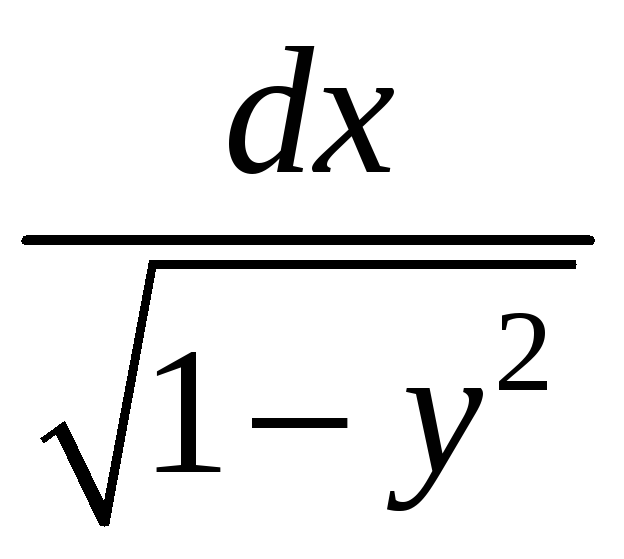, маємо: 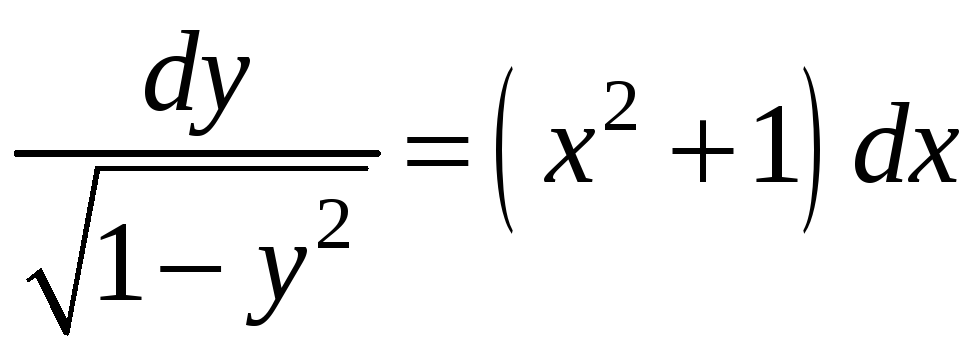. Проінтегруємо і отримаємо загальний інтеграл: 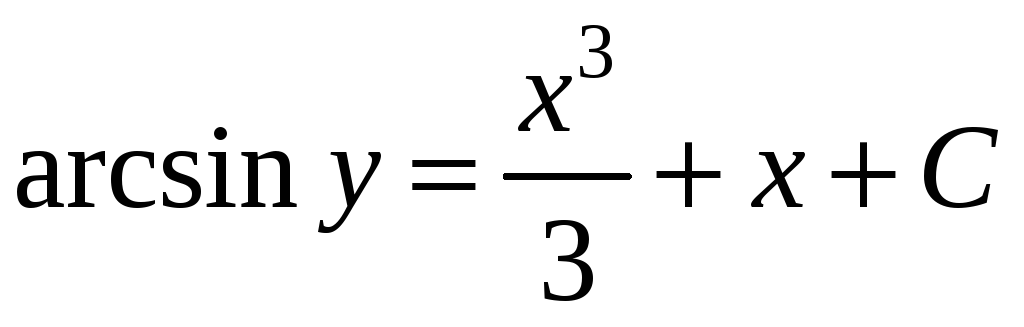або загальний розв’язок:.

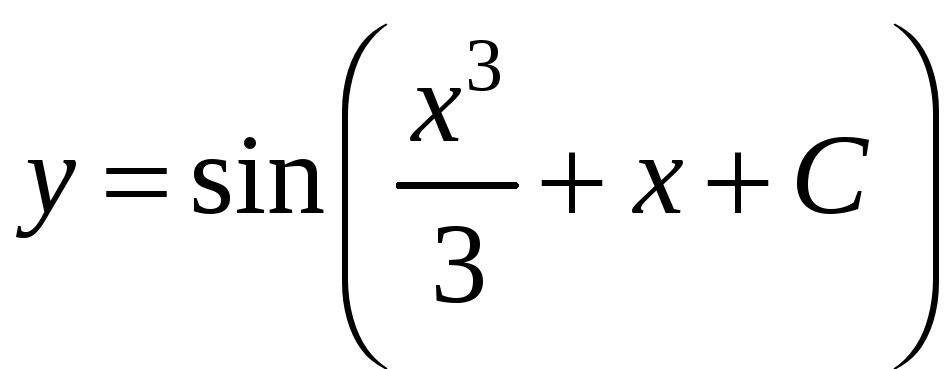Знайдемо особливі розв’язки: .

Приклад. Розв’язати задачу Коші .

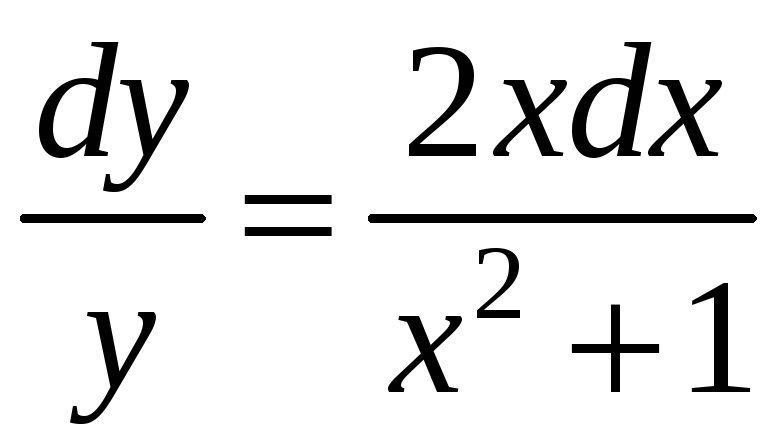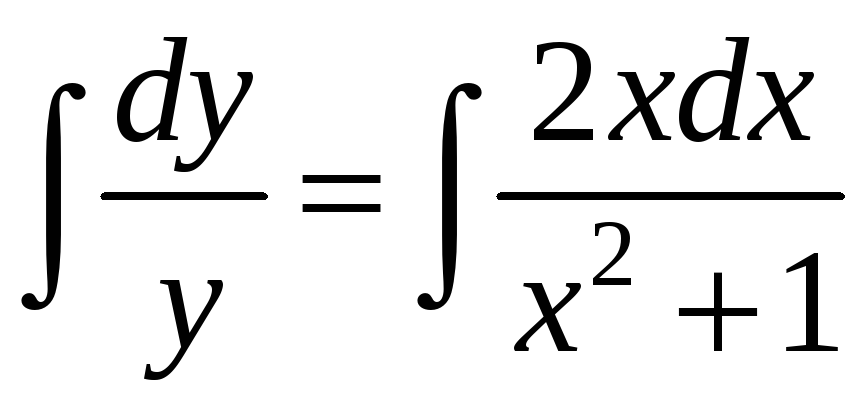Розв’язання. Запишемо рівняння у вигляді і "відокремимо змінні". Отримаємо: ; ; або .

Особливий розв’язок можна приєднати до загального, якщо у сімействі довільна стала зможе також набувати значення . Таким чином, - всі розв’язки диференціального рівняння. Виберемо з цього сімейства частинний розв’язок, що задовольняє початкову умову . У цьому розв’язку стала має бути такою, щоб , тобто . Розв’язок задачі Коші: .

2. Однорідні диференціальні рівняння – це рівняння виду

.

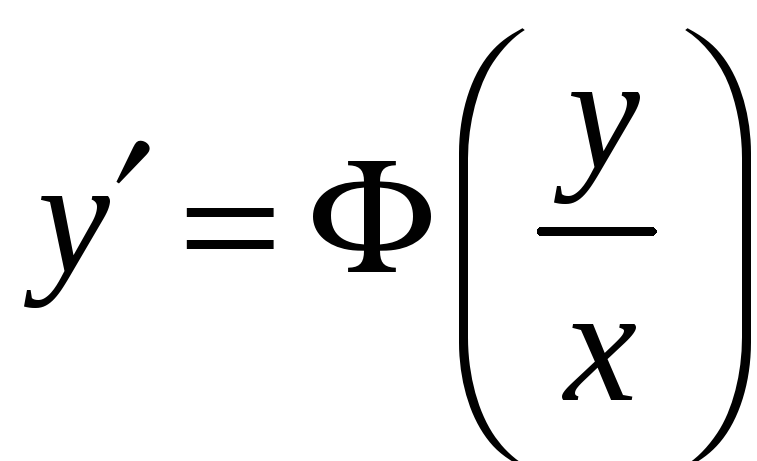Права частина такого рівняння може розглядатися як функція лише одного аргументу . Вважаємо новою невідомою функцією. При цьому , а . Рівняння (2.7) набуває вигляду або 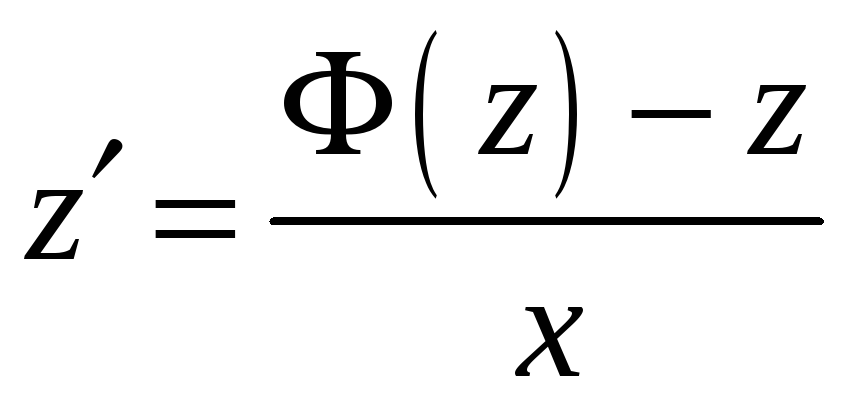, тобто стає рівнянням з відокремлюваними змінними відносно невідомої функції . Після того, як останнє рівняння буде розв’язане, слід повернутись до невідомої функції, замінивши на .

Приклад. Розв’язати диференціальне рівняння .

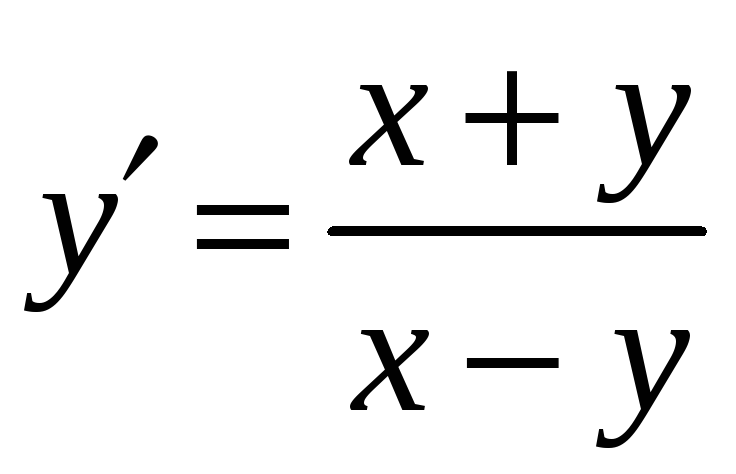Розв’язання. Це однорідне рівняння тому, що розділивши чисельник і знаменник на ми приводимо його до виду 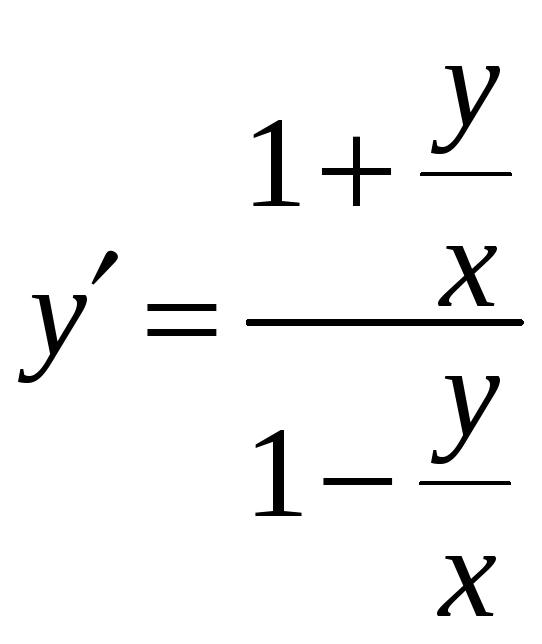. Виконаємо заміну за формулою 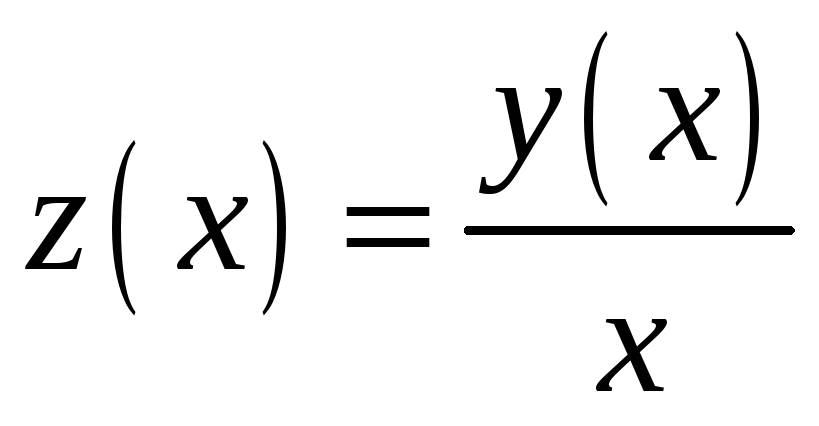. Одержимо рівняння або 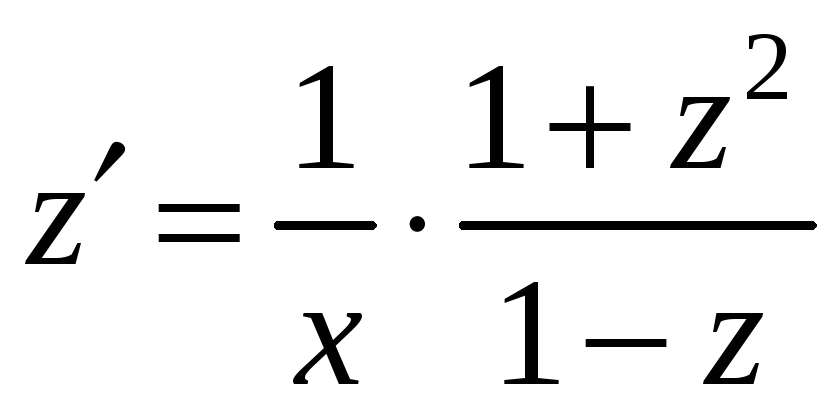. Останнє рівняння з відокремлюваними змінними розв’яжемо за схемою, наведеною в пункті 1.

.

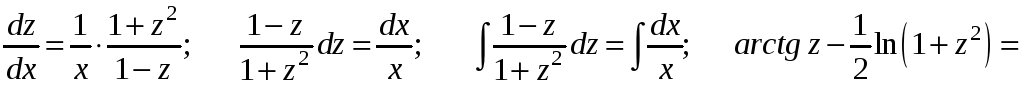
Замінивши на одержимо загальний інтеграл .

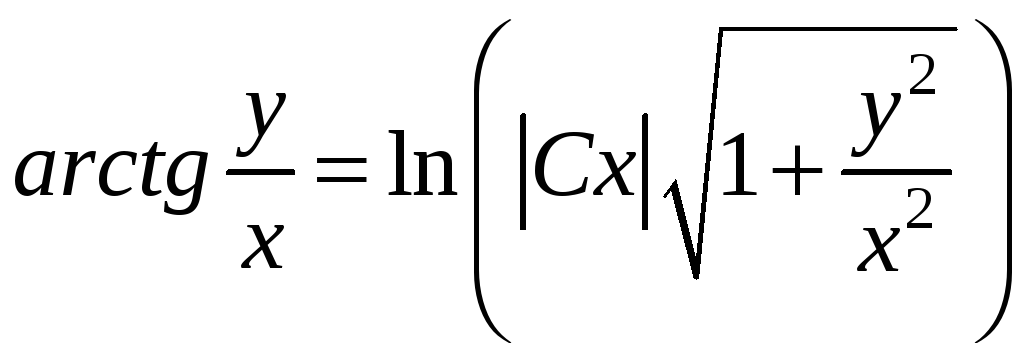3. Лінійне диференціальне рівняння має вигляд

,

де і - задані функції. Будемо шукати розв’язок лінійного рівняння у вигляді , тоді . Підставивши ці вирази в рівняння (2.8) одержимо: або

.

Підберемо функцію так, щоб вираз в дужках дорівнював нулю. Тобто знайдемо функцію як частинний розв’язок диференціального рівняння з відокремлюваними змінними .Після цього знайдену функцію підставимо в рівняння (2.9), яке тоді матиме вигляд . Знайдемо загальний розв’язок останнього рівняння. Запишемо відповідь у вигляді .

Приклад. Розв’язати диференціальне рівняння .

Розв’язання. Це лінійне рівняння, оскільки воно має вигляд (2.8), де - . Виконаємо заміну отримаємо: або . Функцію знайдемо як розв’язок рівняння . Маємо: .

Тоді . Таким чином, одержимо загальний розв’язок .