1. Обчислення площі плоскої фігури.

Ми вже знаємо, як обчислити площу криволінійної трапеції. Застосуємо метод диференціалу для обчислення площі плоскої фігури обмеженої лініями , де при (рис.4).

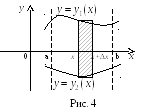
Обчислимо диференціал , замінивши його площею прямокутника, який на рисунку 4 заштриховано.

. Тоді .

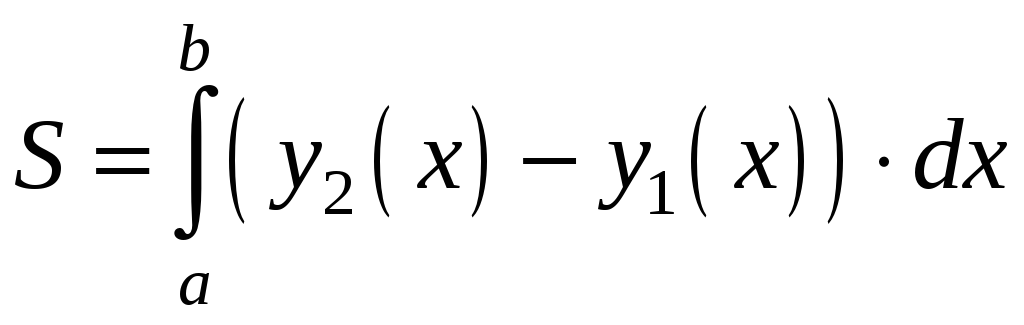Приклад. Обчислити площу фігури, обмеженої лініями , .

Розв’язання. Побудуємо параболу і пряму (рис.5). Точки їх перетину знайдемо як розв’язок системи рівнянь.

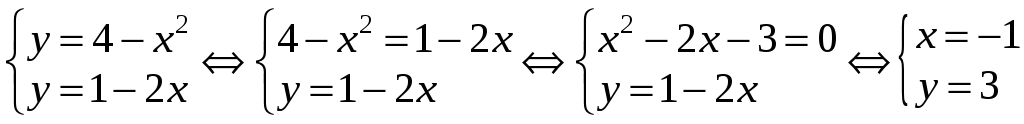або .

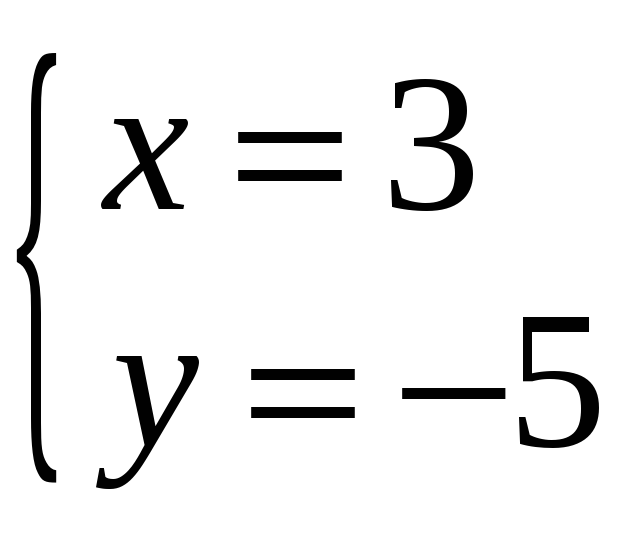Тоді

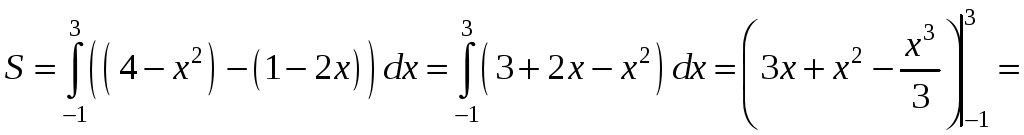
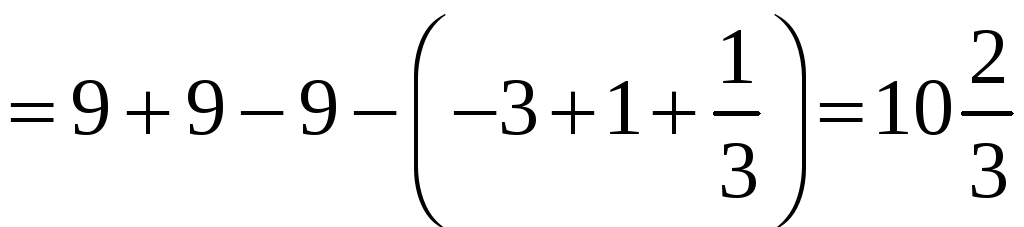квадратних одиниць.

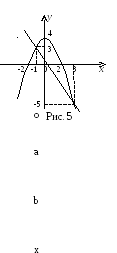
2. Обчислення довжини дуги.

Н ехай рівняння задають лінію, довжину дуги якої між точками і (рис.6) треба знайти. Вважаємо, що точці відповідає значення параметра , а точці - .

Обчислимо диференціал довжини дуги , що дорівнює довжині дуги , де . Замінимо довжину дуги довжиною відрізка : . Таким чином, довжина дуги кривої обчислюється за формулою:

Якщо лінія задана в прямокутній декартовій системі координат рівнянням , то замінивши в рівності (1.14) параметр на , одержимо: .

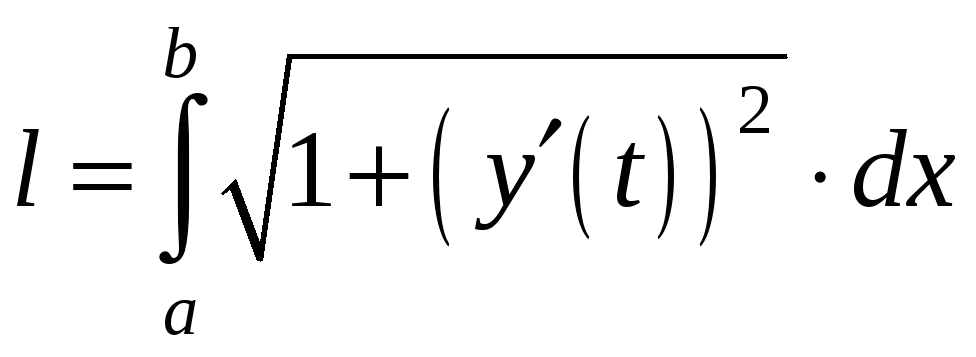Приклад. Знайти довжину першої арки циклоїди: , .

Розв’язання. Знайдемо . Тоді

,

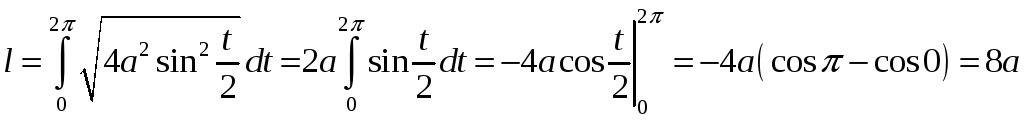одиниць довжини.

2. Обчислення об’єму за площею поперечного перерізу.

Нехай треба обчислити об’єм тіла зображеного на рис.7. Вважаємо, що відома площа перерізу цього тіла будь-якою площиною, перпендикулярною до осі . Ця площа залежить від положення такої площини, тобто вона є функцією .

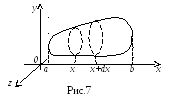
Знайдемо диференціал об’єму , замінивши його на об’єм циліндра, основою якого служить вказаний переріз, а висота дорівнює . Маємо: . Тоді

.

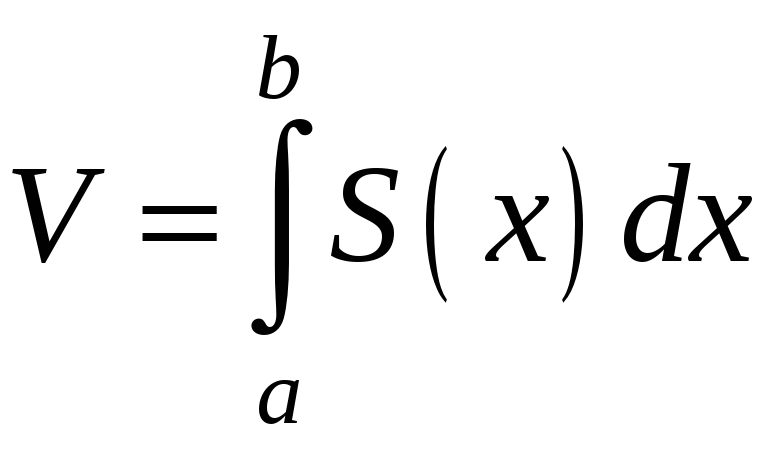Розглянемо фігуру, яка утворена обертанням навколо осі криволінійної трапеції, що обмежена лініями (рис.8). поперечним перерізом такої фігури є круг, радіус якого при заданому дорівнює . Тоді , тому формула (1.15) набуває вигляду .

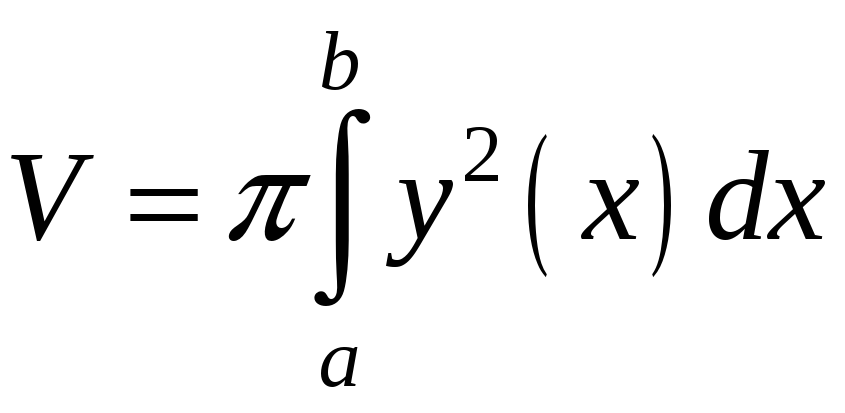Приклад. Знайти об’єм тіла, утвореного обертанням навколо осі фігури, що обмежена лініями .

Розв’язання. 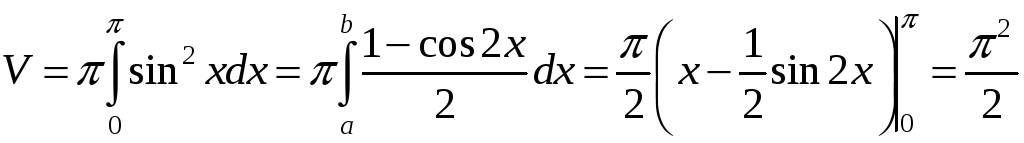кубічних одиниць.

Для більш детального вивчення інтегрального числення рекомендуємо звернутись до навчальних посібників .

Розділ 2. Звичайні диференціальні рівняння

§1. Поняття про диференціальні рівняння

Розглянемо спочатку фізичну задачу, яка приводить до диференціального рівняння. Нехай треба знайти закон, за яким змінюється швидкість тіла ( - час), що рухається по інерції. Цим тілом може бути, наприклад, судно, яке ще рухається після вимикання двигуна. При цьому тіло зазнає опору оточуючого середовища, який є пропорційним до швидкості, тобто дорівнює . Нехай - маса тіла, - прискорення, причому 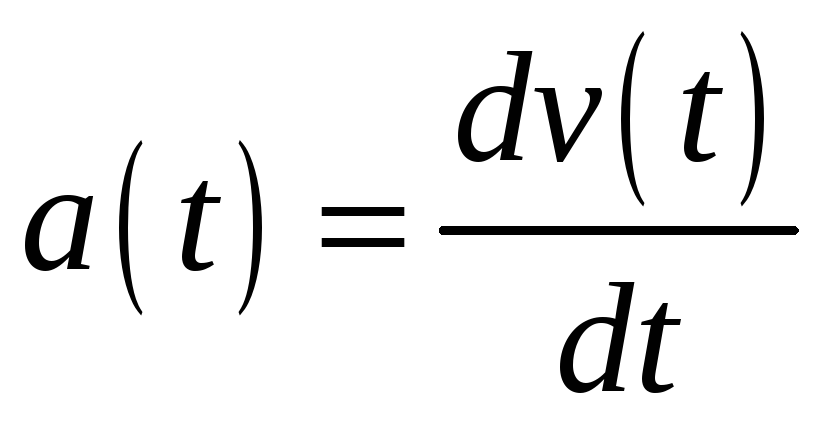. Тоді сила, що діє на тіло у напрямі його руху дорівнює 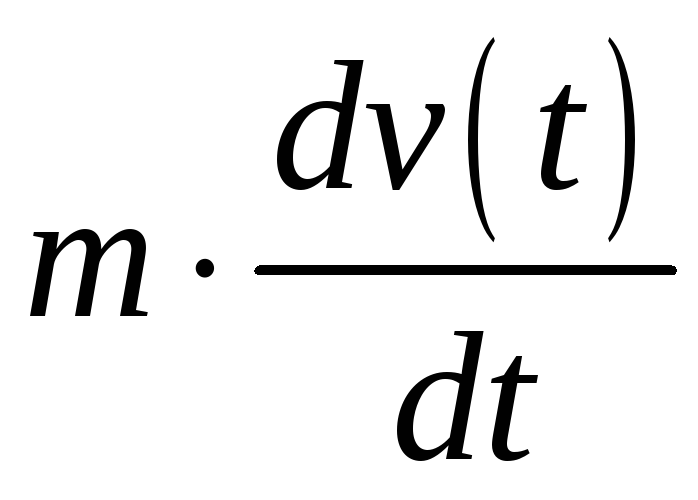. Оскільки ж ця сила за абсолютною величиною дорівнює силі опору середовища, а за напрямом їй протилежна, то отримаємо рівняння

.

Отже шукана функція є розв’язком рівняння (2.1), яке крім самої функції містить також її похідну.

Означення. Звичайним диференціальнім рівнянням називається рівняння, що пов’язує між собою незалежну змінну , невідому функцію та її похідні:

.

Порядком диференціального рівняння називають найвищий з порядків похідних невідомої функції, які воно містить. Рівняння (2.2) - диференціальне рівняння - го порядку.