
- •Г.В. Соколовська с.Ю. Соколовський вища математика
- •Розділ 1. Інтегральне числення
- •§1. Первісна. Невизначений інтеграл та його властивості
- •Властивості невизначеного інтеграла
- •Основні формули інтегрування
- •§2. Метод заміни змінної (підстановки) у невизначеному інтегралі
- •§3. Інтегрування частинами у невизначеному інтегралі
- •§4. Інтегрування деяких виразів, що містять квадратний тричлен
- •§5. Інтегрування деяких ірраціональних і тригонометричних виразів
- •§6. Про функції, інтеграли від яких не виражаються через елементарні функції
- •§7. Визначений інтеграл та його властивості
- •Геометричний зміст визначеного інтеграла
- •Властивості визначеного інтеграла
- •§8. Інтеграл зі змінною верхньою межею
- •§9. Формула Ньютона - Лейбніца
- •§10. Заміна змінної у визначеному інтегралі
- •§11. Інтегрування частинами у визначеному інтегралі
- •§12. Невластиві інтеграли
- •1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
- •2. Інтеграли від розривної функції (невластиві інтеграли роду).
- •§12. Застосування визначеного інтеграла
- •1. Обчислення площі плоскої фігури.
- •2. Обчислення довжини дуги.
- •2. Обчислення об’єму за площею поперечного перерізу.
- •Розділ 2. Звичайні диференціальні рівняння
- •§1. Поняття про диференціальні рівняння
- •§2. Диференціальні рівняння першого порядку
- •§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
- •§4. Лінійні диференціальні рівняння другого порядку.
- •Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
- •Лінійні неоднорідні диференціальні рівняння.
- •Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
- •§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
- •Розділ 3. Ряди
- •§1. Властивості числового ряду.
- •Основні властивості рядів
- •§2. Ряди з додатними членами.
- •§3. Ряди з довільними членами.
- •§4. Ряди з чергуванням знаків.
- •§5. Функціональні ряди.
- •§6. Степеневий ряд.
- •§6. Розвинення функції в степеневий ряд.
§3. Ряди з довільними членами.
Якщо
всі члени числового ряду
![]() від’ємні, то (за теоремою 3.2) питання
про його збіжність вирішується за
допомогою ряду з додатними членами
від’ємні, то (за теоремою 3.2) питання
про його збіжність вирішується за
допомогою ряду з додатними членами
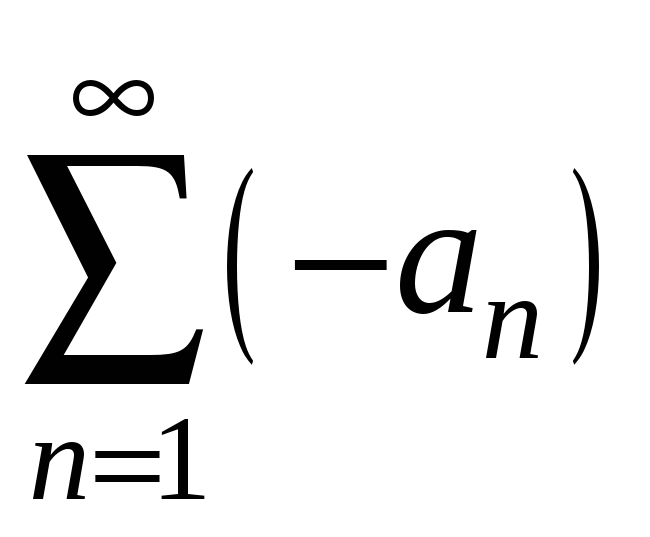 ,
адже
,
адже
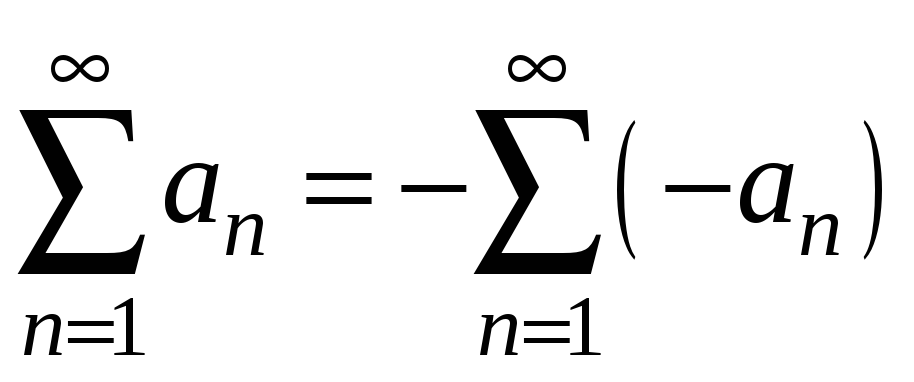 .
Нехай серед членів ряду
.
Нехай серед членів ряду
![]() є і додатні і від’ємні. Якщо від’ємних
членів скінченна кількість, то відкинемо
стільки перших членів ряду, щоб у залишку
були тільки додатні. Дослідимо на
збіжність цей залишок. Аналогічно
досліджується ряд, у якому скінченна
кількість додатних членів. Отже,
досліджуючи ряди з довільними членами,
має сенс розглядати тільки такі ряди
які мають нескінченну кількість як
додатних, так і від’ємних членів. Саме
такі ряди надалі і розглядатимуться.
є і додатні і від’ємні. Якщо від’ємних
членів скінченна кількість, то відкинемо
стільки перших членів ряду, щоб у залишку
були тільки додатні. Дослідимо на
збіжність цей залишок. Аналогічно
досліджується ряд, у якому скінченна
кількість додатних членів. Отже,
досліджуючи ряди з довільними членами,
має сенс розглядати тільки такі ряди
які мають нескінченну кількість як
додатних, так і від’ємних членів. Саме
такі ряди надалі і розглядатимуться.
Теорема
3.14 Нехай
числовий ряд
![]() такий, що ряд складений з модулів його
членів
такий, що ряд складений з модулів його
членів
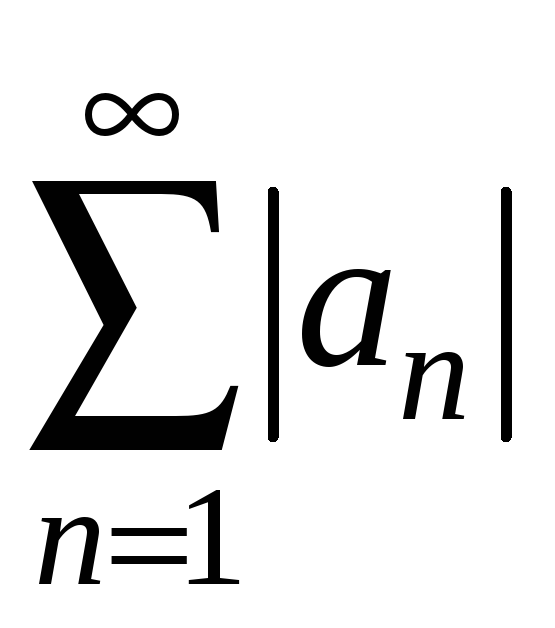 є збіжним. Тоді збігається і ряд
є збіжним. Тоді збігається і ряд
![]() .
.
Доведення.
Нехай
![]() -
-
![]() - на часткова сума ряду
- на часткова сума ряду
![]() ,
а
,
а
![]() -
-
![]() - на часткова сума ряду
- на часткова сума ряду
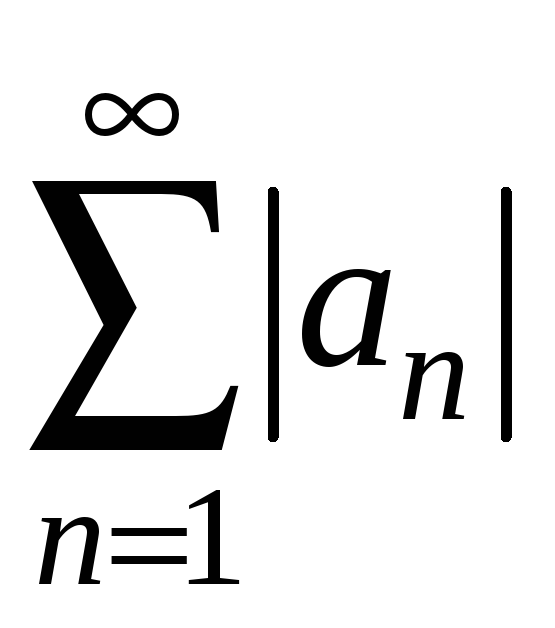 .
Позначимо через
.
Позначимо через
![]() суму додатних членів серед
суму додатних членів серед
![]() перших членів ряду
перших членів ряду
![]() ,
а через
,
а через
![]() - суму модулів від’ємних членів. Тоді
- суму модулів від’ємних членів. Тоді
![]() ,
,
![]() .
Оскільки ряд
.
Оскільки ряд
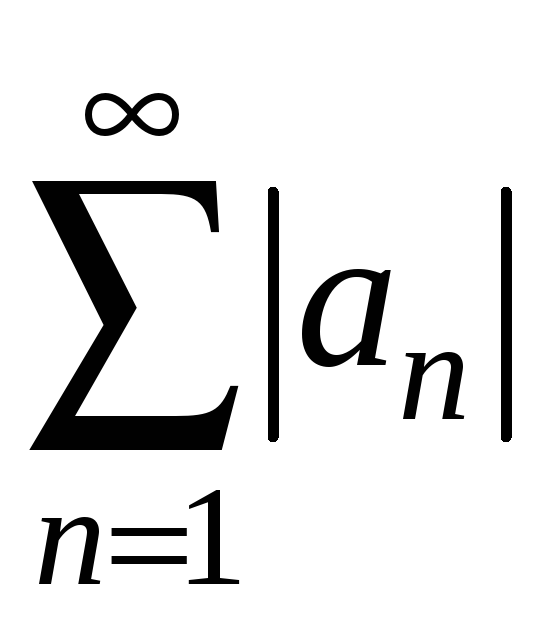 має суму (позначимо її через
має суму (позначимо її через
![]() ),
то
),
то
![]() ,
,
![]() .
Таким чином, послідовності
.
Таким чином, послідовності
![]() і
і
![]() монотонні і обмеженні. Отже кожна з них
має границю. Позначимо ці границі через
монотонні і обмеженні. Отже кожна з них
має границю. Позначимо ці границі через
![]() і
і
![]() відповідно. Тоді існує границя
відповідно. Тоді існує границя
![]() послідовності часткових сум ряду
послідовності часткових сум ряду
![]() :
:
![]() .
Тобто цей ряд збігається.
.
Тобто цей ряд збігається.
Зауваження. Ряд може збігатися і в тому випадку, коли складений з модулів його членів ряд розбігається.
Означення.
Якщо
ряд, складений з модулів членів ряду
![]() збігається, сам ряд
збігається, сам ряд
![]() називається абсолютно збіжним. Якщо
сам ряд
називається абсолютно збіжним. Якщо
сам ряд
![]() збігається, а ряд
збігається, а ряд
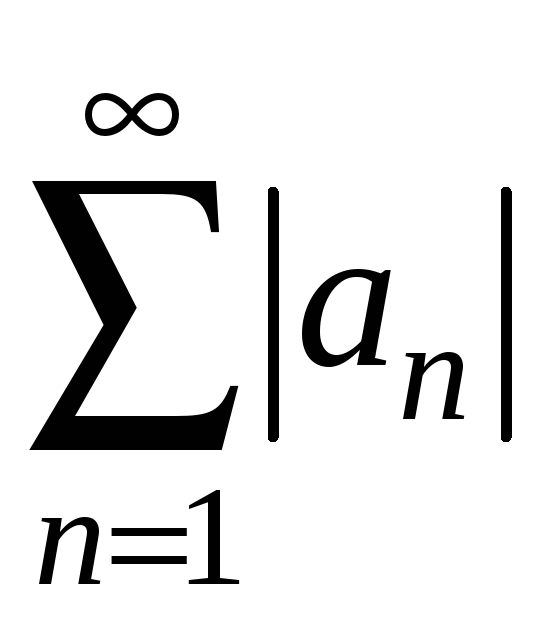 розбігається, то ряд
розбігається, то ряд
![]() називають умовно збіжним.
називають умовно збіжним.
§4. Ряди з чергуванням знаків.
Розглянемо
ряд, члени якого по черзі то додатні, то
від’ємні. Тобто з числової послідовності
додатних чисел
![]()
![]() складаємо ряд виду
складаємо ряд виду
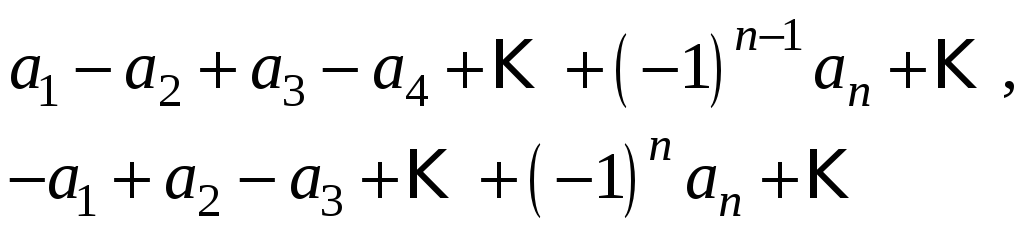 або
або
![]()
Назвемо його рядом з чергуванням знаків.
Теорема 3.15 (ознака Лейбніца). Якщо ряд (3.6) такий, що
1) модулі
його членів спадають при зростанні
номеру, тобто
![]() ,
,
2)
![]()
то ряд збігається.
Доведення.
Розглянемо ряд
![]()
![]() з чергуванням знаків. Запишемо його
часткову суму з парним номером
з чергуванням знаків. Запишемо його
часткову суму з парним номером
![]() :
:
![]() .
З першої умови теореми випливає, що
.
З першої умови теореми випливає, що
![]() .
Тоді
.
Тоді
![]() ,
і ця часткова сума зростає зі збільшенням
,
і ця часткова сума зростає зі збільшенням
![]() .
З іншого боку
.
З іншого боку
![]()
![]() .
Отже, послідовність
.
Отже, послідовність
![]() монотонна і обмежена
монотонна і обмежена
![]() .
Тоді вона має границю
.
Тоді вона має границю
![]() ,
,
![]() .
Розглянемо тепер часткову суму з непарним
номером:
.
Розглянемо тепер часткову суму з непарним
номером:
![]() .
Тоді, враховуючи другу умову теореми,
маємо
.
Тоді, враховуючи другу умову теореми,
маємо
![]()
![]() .
Отже ряд
.
Отже ряд
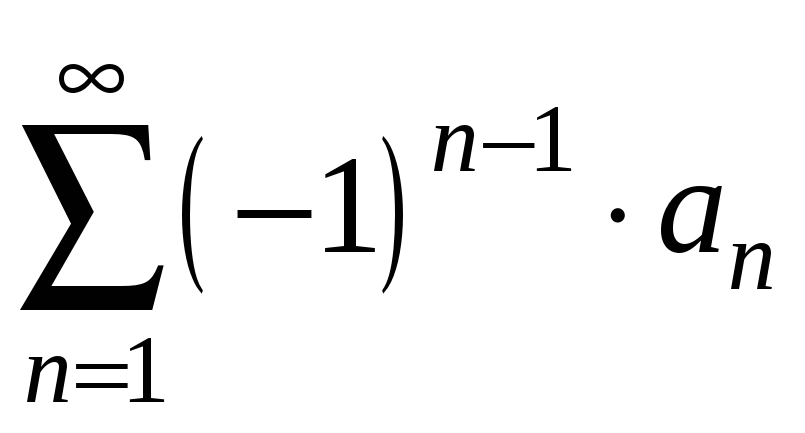 збігається і його сума не перевищує
першого члена
збігається і його сума не перевищує
першого члена
![]() .
.
Зауваження.
1. Ознака Лейбніца залишається справедливою
і в тому випадку, якщо нерівність
![]() виконується починаючи з деякого номера.
виконується починаючи з деякого номера.
2. Не так
часто зустрічаються ряди, суму яких
можна точно обчислити. Найчастіше при
розв’язуванні практичних задач діють
так: з’ясувавши, що ряд збігається,
замінюють його суму
![]() - ною частковою сумою
- ною частковою сумою
![]() .
Адже при достатньо великих
.
Адже при достатньо великих
![]() справедлива наближена рівність
справедлива наближена рівність
![]() .
Похибка цього наближення дорівнює сумі
залишку ряду
.
Похибка цього наближення дорівнює сумі
залишку ряду
![]() .
Тому постає питання про оцінку цього
залишку. Для ряду, що збігається за
ознакою Лейбніца, це питання вирішується
досить просто. Адже для залишку
.
Тому постає питання про оцінку цього
залишку. Для ряду, що збігається за
ознакою Лейбніца, це питання вирішується
досить просто. Адже для залишку
![]()
![]() також виконані умови теореми
також виконані умови теореми
![]() .
Тоді його сума
.
Тоді його сума
![]() задовольняє нерівність
задовольняє нерівність
![]() .
Таким чином, похибка має знак першого
відкинутого члена ряду і не перевищує
його за абсолютною величиною.
.
Таким чином, похибка має знак першого
відкинутого члена ряду і не перевищує
його за абсолютною величиною.
Приклади. Дослідити збіжність рядів:
1.
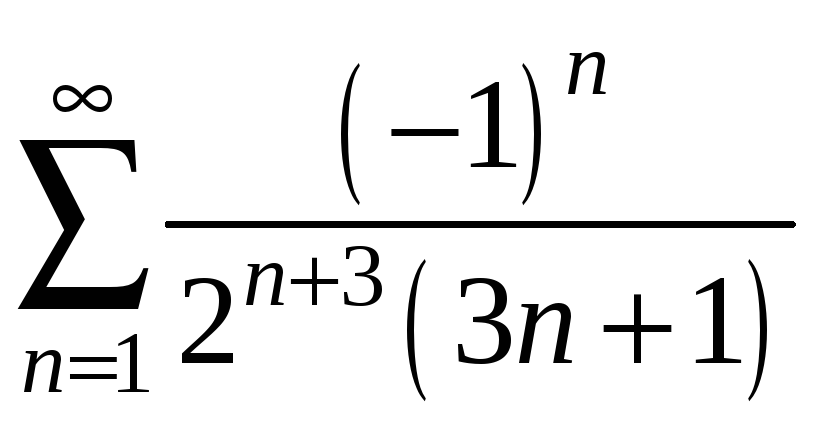 .
.
Розглянемо
ряд з модулів
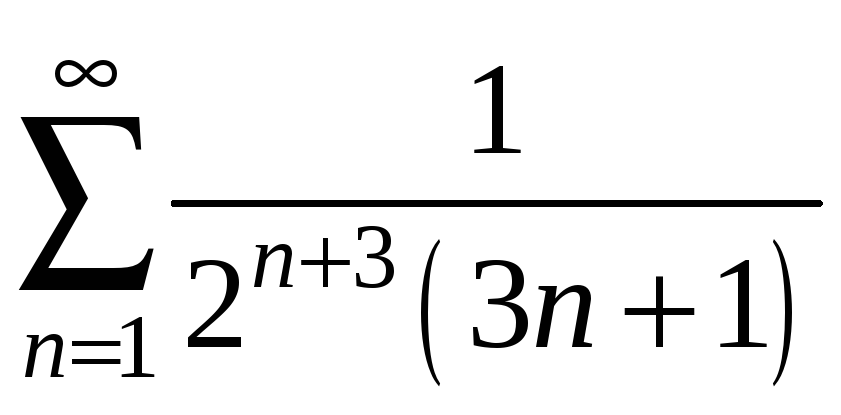 .
Дослідимо його збіжність за ознакою
Даламбера. Запишемо загальний член ряду
.
Дослідимо його збіжність за ознакою
Даламбера. Запишемо загальний член ряду
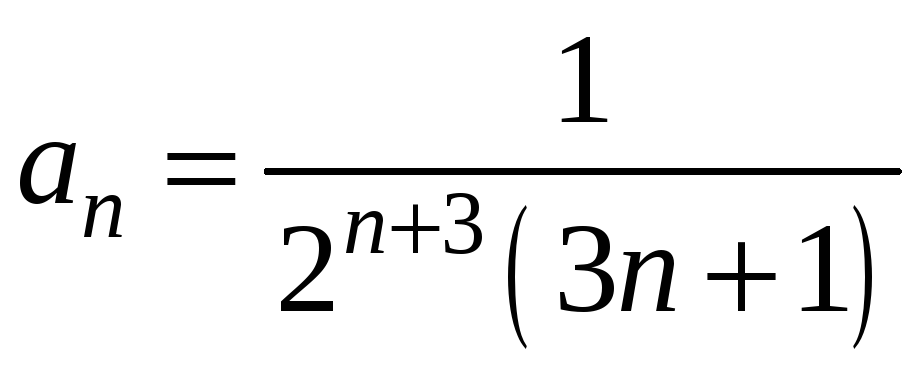 і наступний
і наступний
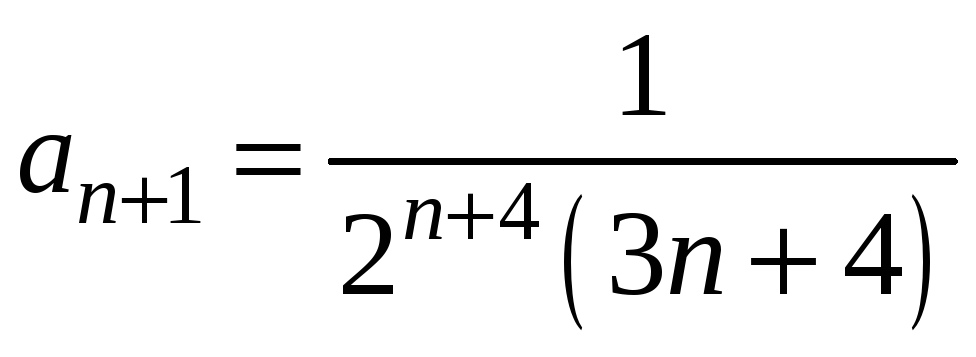 .
Знайдемо
.
Знайдемо
 .
Отже, ряд з модулів збігається. Тоді
досліджуваний ряд з чергуванням знаків
збігається абсолютно.
.
Отже, ряд з модулів збігається. Тоді
досліджуваний ряд з чергуванням знаків
збігається абсолютно.
2.
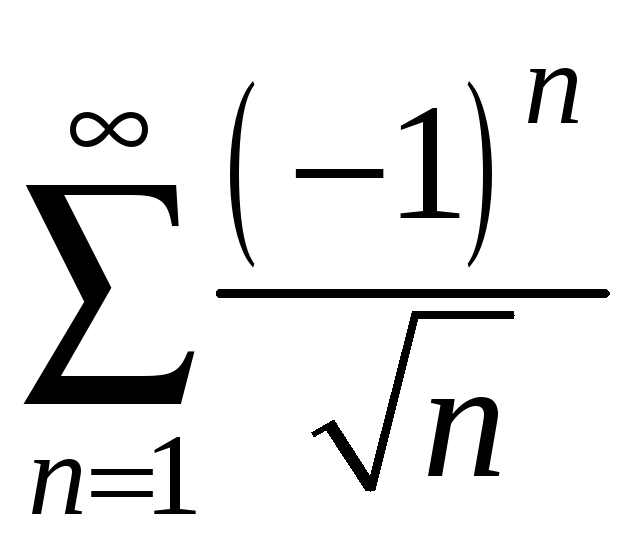 .
.
Ряд з
модулів
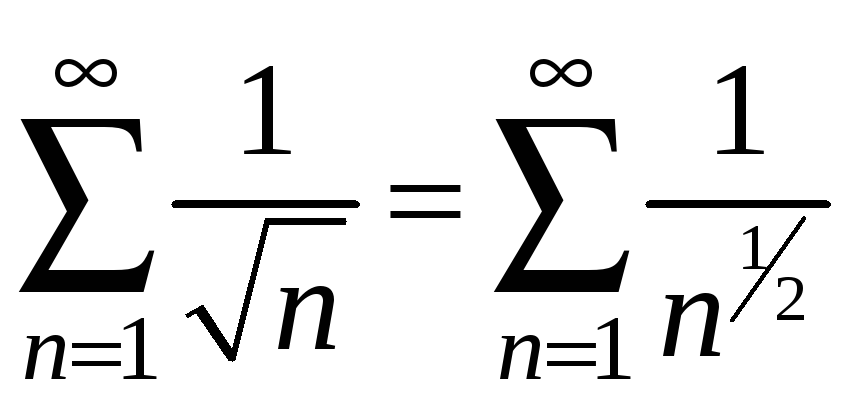 розбігається
розбігається
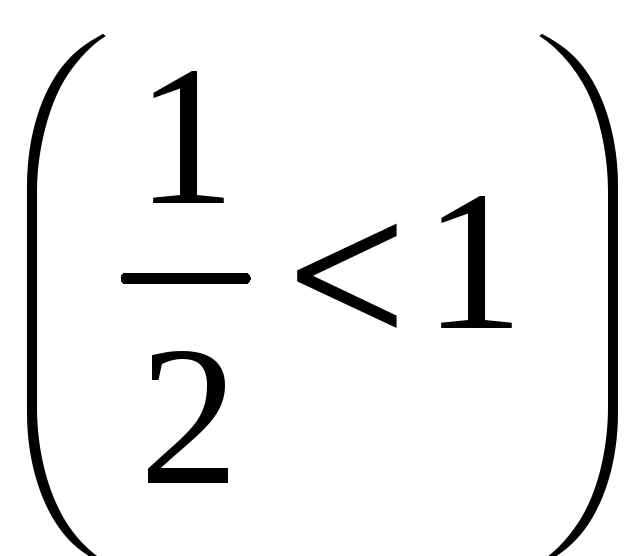 .
Це означає, що досліджуваний ряд з
чергуванням знаків не є абсолютно
збіжним. Але він може збігатися умовно.
Застосуємо ознаку Лейбніца:
.
Це означає, що досліджуваний ряд з
чергуванням знаків не є абсолютно
збіжним. Але він може збігатися умовно.
Застосуємо ознаку Лейбніца:
1)
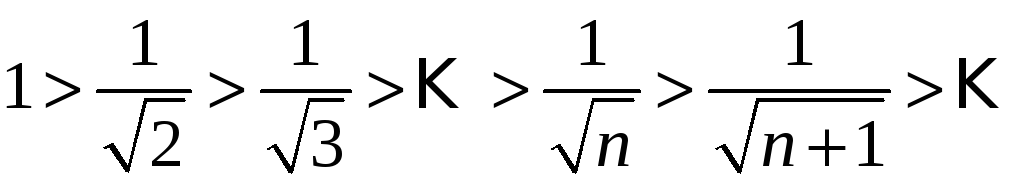 ,
,
2)
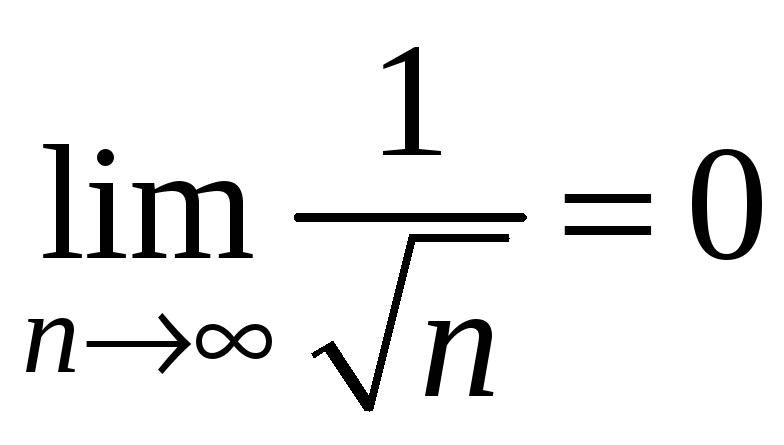 .
.
Отже
ряд
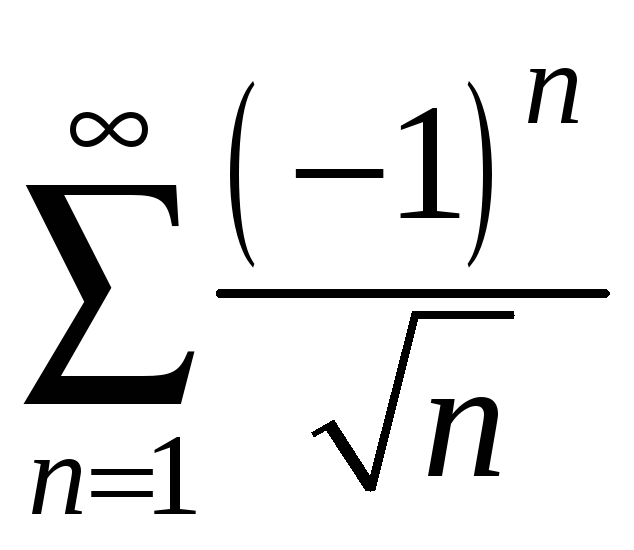 збігається умовно.
збігається умовно.
