
- •Г.В. Соколовська с.Ю. Соколовський вища математика
- •Розділ 1. Інтегральне числення
- •§1. Первісна. Невизначений інтеграл та його властивості
- •Властивості невизначеного інтеграла
- •Основні формули інтегрування
- •§2. Метод заміни змінної (підстановки) у невизначеному інтегралі
- •§3. Інтегрування частинами у невизначеному інтегралі
- •§4. Інтегрування деяких виразів, що містять квадратний тричлен
- •§5. Інтегрування деяких ірраціональних і тригонометричних виразів
- •§6. Про функції, інтеграли від яких не виражаються через елементарні функції
- •§7. Визначений інтеграл та його властивості
- •Геометричний зміст визначеного інтеграла
- •Властивості визначеного інтеграла
- •§8. Інтеграл зі змінною верхньою межею
- •§9. Формула Ньютона - Лейбніца
- •§10. Заміна змінної у визначеному інтегралі
- •§11. Інтегрування частинами у визначеному інтегралі
- •§12. Невластиві інтеграли
- •1. Інтеграли з нескінченними межами інтегрування (невластиві інтеграли і роду).
- •2. Інтеграли від розривної функції (невластиві інтеграли роду).
- •§12. Застосування визначеного інтеграла
- •1. Обчислення площі плоскої фігури.
- •2. Обчислення довжини дуги.
- •2. Обчислення об’єму за площею поперечного перерізу.
- •Розділ 2. Звичайні диференціальні рівняння
- •§1. Поняття про диференціальні рівняння
- •§2. Диференціальні рівняння першого порядку
- •§2. Диференціальні рівняння другого порядку. Рівняння, що допускають зниження порядку.
- •§4. Лінійні диференціальні рівняння другого порядку.
- •Лінійні однорідні диференціальні рівняння зі сталими коефіцієнтами.
- •Лінійні неоднорідні диференціальні рівняння.
- •Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами і спеціальним виглядом правої частини.
- •§5. Системи диференціальних рівнянь першого порядку. Системи лінійних рівнянь зі сталими коефіцієнтами.
- •Розділ 3. Ряди
- •§1. Властивості числового ряду.
- •Основні властивості рядів
- •§2. Ряди з додатними членами.
- •§3. Ряди з довільними членами.
- •§4. Ряди з чергуванням знаків.
- •§5. Функціональні ряди.
- •§6. Степеневий ряд.
- •§6. Розвинення функції в степеневий ряд.
Основні властивості рядів
Теорема
3.2
Якщо всі члени збіжного ряду з сумою
![]() помножити на одне й теж число
помножити на одне й теж число
![]() ,
то одержимо збіжний ряд, сума якого
дорівнює
,
то одержимо збіжний ряд, сума якого
дорівнює
![]() .
.
Доведення.
Нехай ряд
![]() збігається,
збігається,
![]() - його сума,
- його сума,
![]() -
-
![]() -
на часткова сума. Знайдемо границю
-
на часткова сума. Знайдемо границю
![]() - ної часткової суми ряду, який отримаємо
після множення кожного члена на
- ної часткової суми ряду, який отримаємо
після множення кожного члена на
![]() :
:
![]() .
.
Теорему доведено.
Теорема
3.3
Якщо ряди
![]() і
і
![]() збігаються і їх суми відповідно дорівнюють
збігаються і їх суми відповідно дорівнюють
![]() і
і
![]() ,
то збігаються ряди, отримані їх по
членним додаванням і відніманням. При
цьому
,
то збігаються ряди, отримані їх по
членним додаванням і відніманням. При
цьому
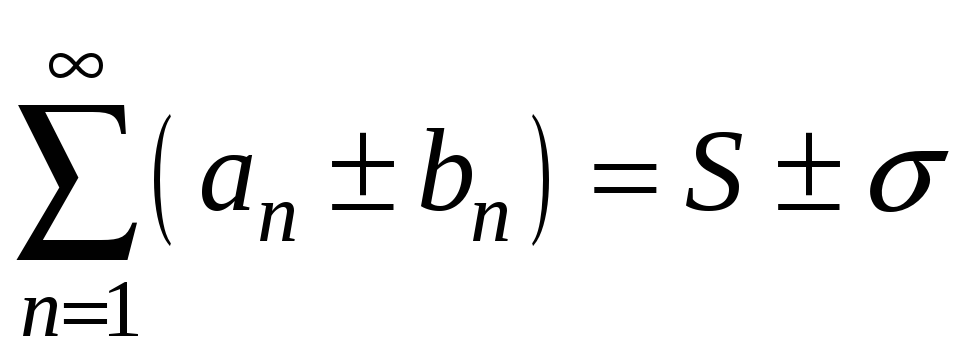 .
.
Доведення.
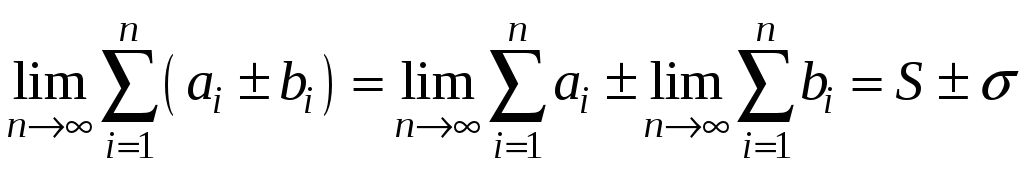 ,
що і треба довести.
,
що і треба довести.
Означення.
В числовому ряді (3.1) відкинемо перші
![]() членів. Ряд, що залишиться:
членів. Ряд, що залишиться:
![]() назвемо залишком ряду (3.1) після
назвемо залишком ряду (3.1) після
![]() -го члена.
-го члена.
Теорема 3.4 Ряд (3.1) і його залишок збігаються або розбігаються одночасно.
Доведення.
Зафіксуємо номер
![]() .
.
![]() -
-
![]() - на часткова сума ряду (3.1),
- на часткова сума ряду (3.1),
![]() - часткова сума його залишку. Тоді
- часткова сума його залишку. Тоді
![]() .
Нехай ряд (3.1) збігається, і його сума
дорівнює
.
Нехай ряд (3.1) збігається, і його сума
дорівнює
![]() ,
тоді існує скінченна границя
,
тоді існує скінченна границя
![]() .
Тобто залишок також збігається. Нехай
тепер збігається залишок ряду (3.1) після
.
Тобто залишок також збігається. Нехай
тепер збігається залишок ряду (3.1) після
![]() -
го члена. Позначимо його суму через
-
го члена. Позначимо його суму через
![]() .
Тоді
.
Тоді
![]() -
скінченне число. Остання рівність
означає, що ряд (3.1) збігається, його суму
позначимо через
-
скінченне число. Остання рівність
означає, що ряд (3.1) збігається, його суму
позначимо через
![]() .
Отже
.
Отже
![]() .
Нехай тепер ряд (3.1) розбігається. Тоді
розбігається і його залишок. Адже у
випадку збіжності залишку збігався б
і ряд (3.1). По аналогії отримаємо: із
розбіжності залишку випливає розбіжність
ряду. Теорему доведено.
.
Нехай тепер ряд (3.1) розбігається. Тоді
розбігається і його залишок. Адже у
випадку збіжності залишку збігався б
і ряд (3.1). По аналогії отримаємо: із
розбіжності залишку випливає розбіжність
ряду. Теорему доведено.
Наслідки. 1.Теорему 3.4 можна розуміти ще і таким чином: відкидання декількох перших членів ряду або додавання на початку ряду скінченної кількості нових членів не впливає на його збіжність, а може змінити лише його суму.
2. Числовий
ряд збігається тоді і тільки тоді, коли
сума його залишку
![]() прямує до нуля коли
прямує до нуля коли
![]() .
Адже з рівності
.
Адже з рівності
![]() випливає:
випливає:
![]() ;
;
![]() .
.
Теорема
3.5
(необхідна умова збіжності ряду) Якщо
ряд
![]() збігається, то його загальний член
прямує до 0 при
збігається, то його загальний член
прямує до 0 при
![]() .
.
Доведення.
Нехай
![]() - сума ряду. Оскільки
- сума ряду. Оскільки
![]() ,
то
,
то
![]() .
.
Зауваження.
Доводити збіжність рядів за допомогою
цієї теореми неможливо, можна лише
стверджувати, що ряд розбігається, якщо
![]() .
Адже у будь-якого збіжного ряду
.
Адже у будь-якого збіжного ряду
![]() .
.
Приклади.
Дослідити збіжність ряду
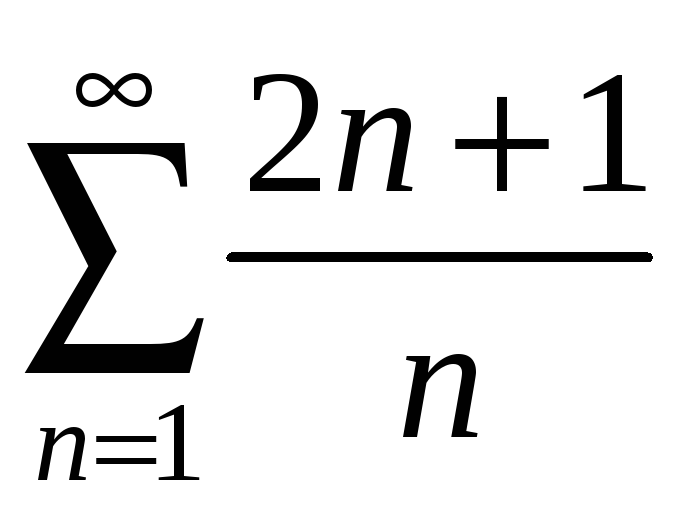 .
.
Розв’язання.
![]() .
Ряд розбігається.
.
Ряд розбігається.
Теорема
3.6
Якщо ряд
![]() збігається, то можна (не переставляючи
його члени) об’єднувати їх у групи зі
скінченною кількістю членів за допомогою
дужок. Ця операція не порушує збіжності
ряду і не змінює його суму.
збігається, то можна (не переставляючи
його члени) об’єднувати їх у групи зі
скінченною кількістю членів за допомогою
дужок. Ця операція не порушує збіжності
ряду і не змінює його суму.
§2. Ряди з додатними членами.
Розглянемо ряд, всі члени якого додатні
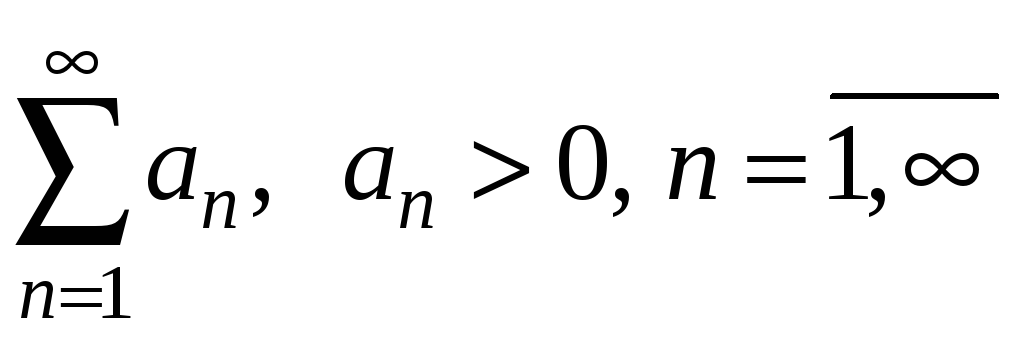 .
.
![]()
Теорема
3.7
(необхідна і достатня умова збіжності
ряду з додатними членами). Для того, щоб
ряд (3.2) збігався необхідно і достатньо,
щоб послідовність його часткових сум
![]() була обмежена зверху, тобто існувало
таке число
була обмежена зверху, тобто існувало
таке число
![]() ,
що
,
що
![]() .
.
Доведення.
Необхідність.
Нехай
ряд (3.2) збігається. Тоді послідовність
його часткових сум має скінченну границю.
Ця послідовність монотонно зростає,
адже
![]() .
Тоді вона має бути обмежена зверху, адже
у протилежному випадку
.
Тоді вона має бути обмежена зверху, адже
у протилежному випадку
![]() .
.
Достатність.
Якщо послідовність
![]() обмежена зверху, то враховуючи, що вона
монотонно зростає, одержимо: ця
послідовність має скінченну границю
за теоремою Вейерштраса. Отже, ряд
збігається.
обмежена зверху, то враховуючи, що вона
монотонно зростає, одержимо: ця
послідовність має скінченну границю
за теоремою Вейерштраса. Отже, ряд
збігається.
Теорема
3.8
(інтегральна ознака збіжності). Нехай
члени ряду (3.2) співпадають зі значенням
неперервної, незростаючої, невід’ємної
при
![]() функції
функції
![]() ,
якщо
,
якщо
![]() ,
тобто
,
тобто
![]() .
Тоді ряд (3.2) збігається або розбігається
одночасно з невластивим інтегралом
.
Тоді ряд (3.2) збігається або розбігається
одночасно з невластивим інтегралом
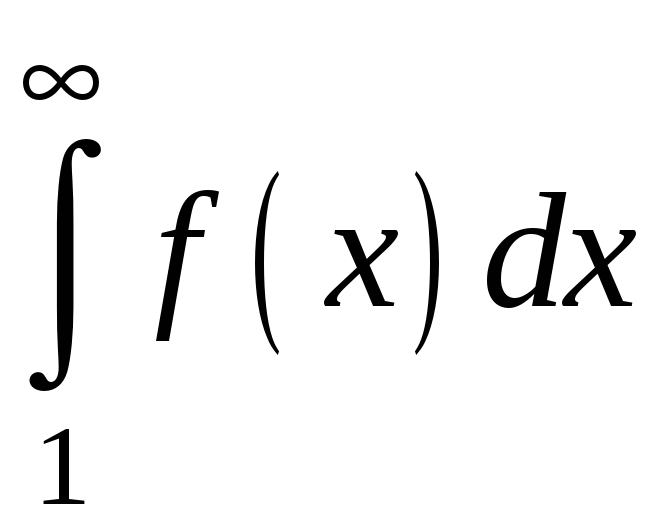 .
.
Д оведення.
Нехай
оведення.
Нехай
![]() - деяке натуральне число. Розглянемо
криволінійну трапецію, обмежену лініями
- деяке натуральне число. Розглянемо
криволінійну трапецію, обмежену лініями
![]() .
Її площа дорівнює визначеному інтегралу
.
Її площа дорівнює визначеному інтегралу
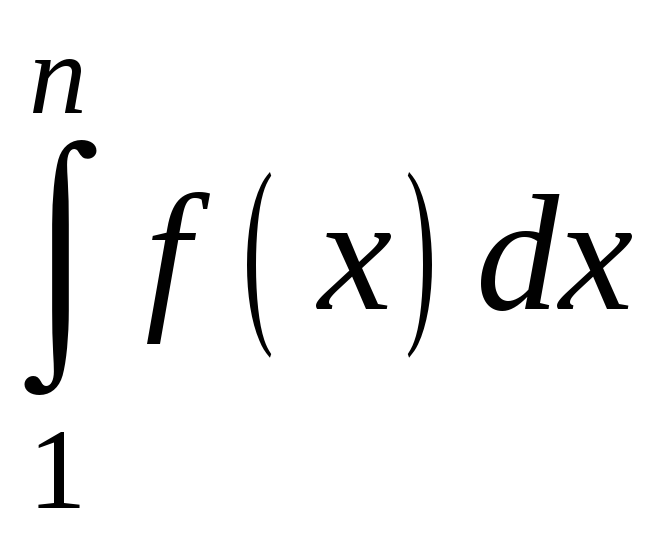 .
.
Заключимо
цю криволінійну трапецію в ступінчасту
фігуру (див. рис. 3.1 для
![]() ),
що складається з прямокутників, одна
зі сторін яких дорівнює
),
що складається з прямокутників, одна
зі сторін яких дорівнює
![]() ,
а друга
,
а друга
![]() .
Тоді площа цієї фігури дорівнює
.
Тоді площа цієї фігури дорівнює
![]() .
Розглянемо також вписану у криволінійну
трапецію ступінчасту фігуру, зображену
на рисунку 3.2. Її площа:
.
Розглянемо також вписану у криволінійну
трапецію ступінчасту фігуру, зображену
на рисунку 3.2. Її площа:
![]() .
Оскільки
.
Оскільки
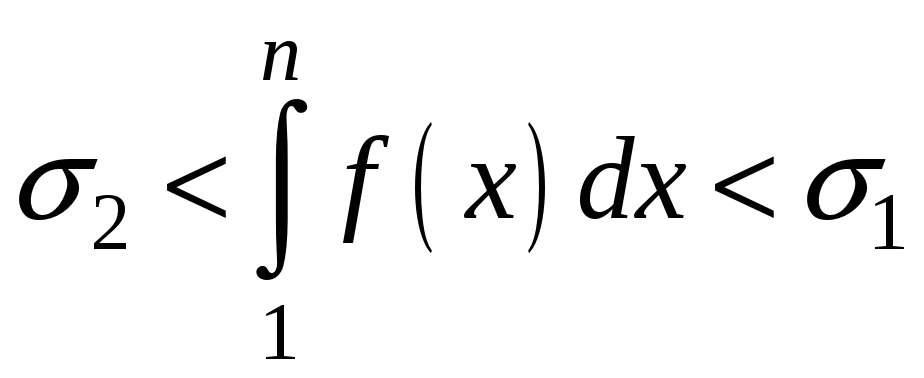 ,
то
,
то
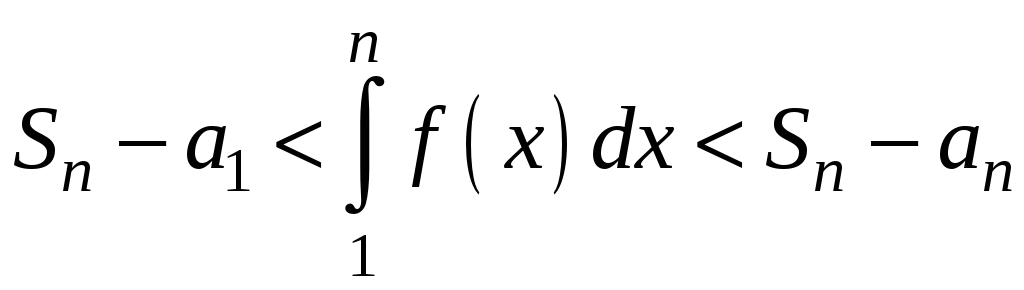 ,
де
,
де
![]() -
на часткова сума ряду (3.2). З останньої
нерівності маємо:
-
на часткова сума ряду (3.2). З останньої
нерівності маємо:
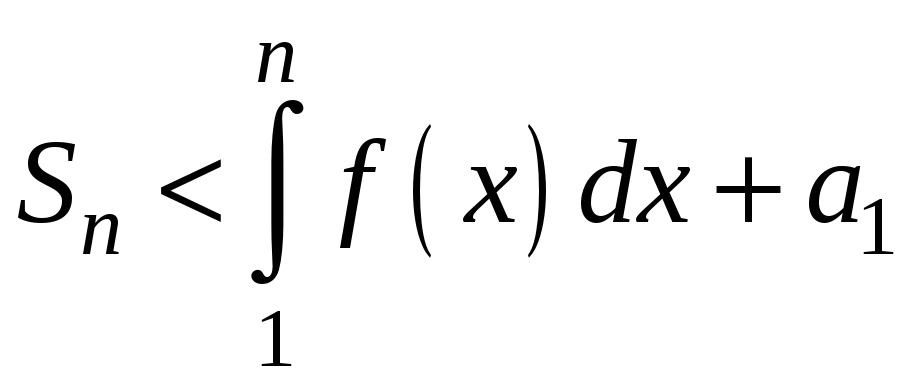 ;
;
![]()
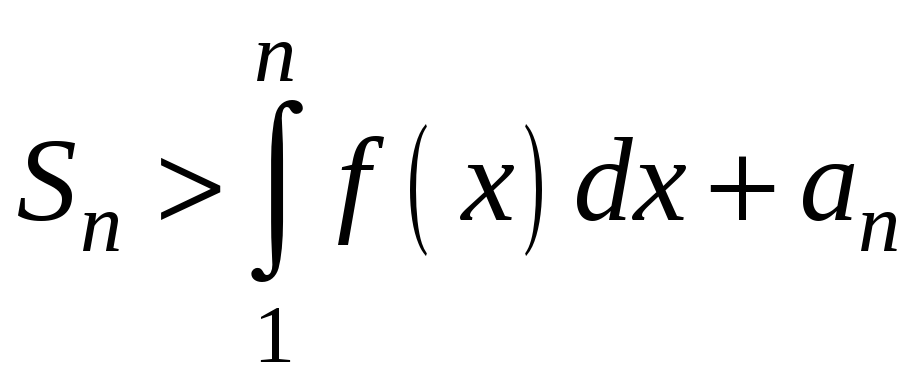 .
.
![]()
Нехай
невластивий інтеграл
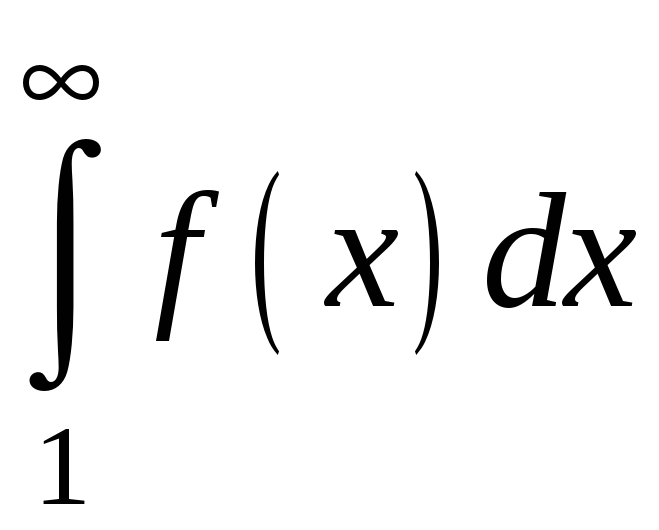 збігається, тоді нескінченна криволінійна
трапеція, побудована на проміжку
збігається, тоді нескінченна криволінійна
трапеція, побудована на проміжку
![]() ,
має скінченну площу
,
має скінченну площу
![]() .
Отже
.
Отже
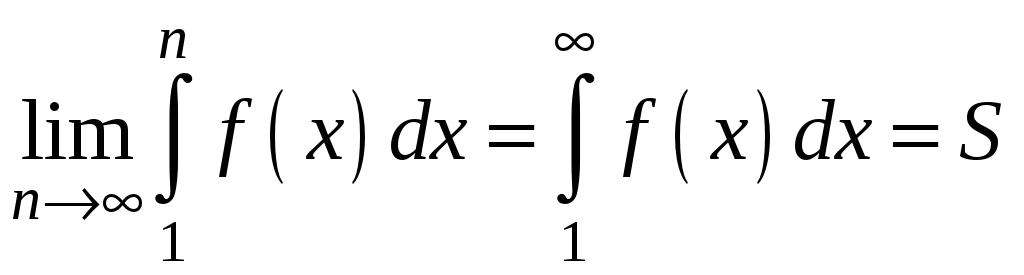 ,
,
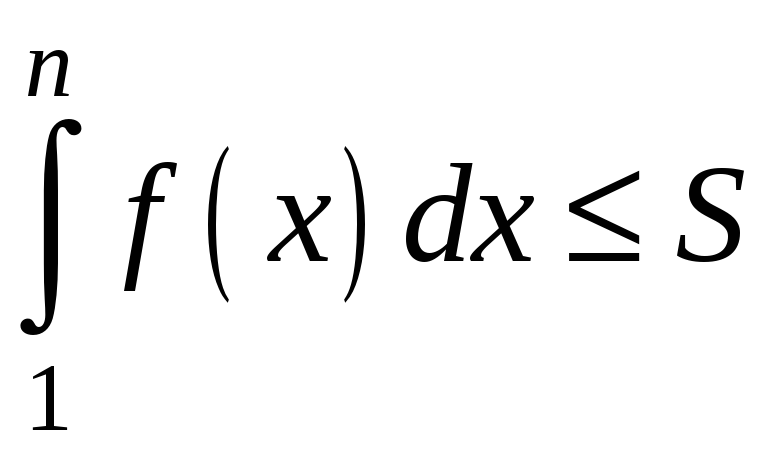 .
Тоді з нерівності (3.3) маємо:
.
Тоді з нерівності (3.3) маємо:
![]() ,
тобто часткові суми ряду (3.2) обмежені
зверху. Таким чином, ряд збігається.
Якщо невластивий інтеграл
,
тобто часткові суми ряду (3.2) обмежені
зверху. Таким чином, ряд збігається.
Якщо невластивий інтеграл
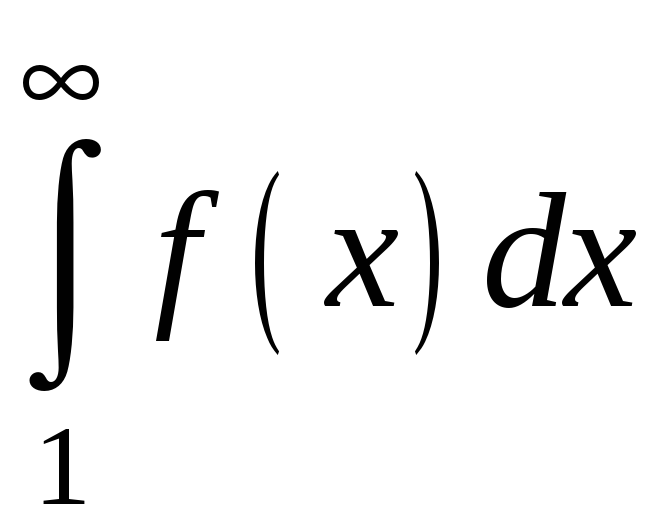 розбігається , тобто
розбігається , тобто
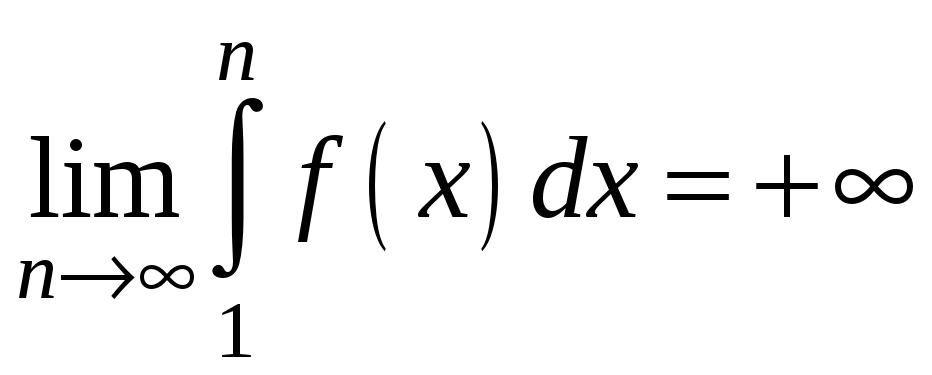 ,
то з нерівності (3.4) випливає, що
,
то з нерівності (3.4) випливає, що
![]() необмежена. Отже ряд розбігається. Нехай
тепер збігається ряд (3.2), тоді збігається
і невластивий інтеграл. Адже у протилежному
випадку розбігався б і ряд. По аналогії
доводиться той факт, що із розбіжності
ряду випливає розбіжність інтегралу.
необмежена. Отже ряд розбігається. Нехай
тепер збігається ряд (3.2), тоді збігається
і невластивий інтеграл. Адже у протилежному
випадку розбігався б і ряд. По аналогії
доводиться той факт, що із розбіжності
ряду випливає розбіжність інтегралу.
Приклад.
Дослідити збіжність ряду
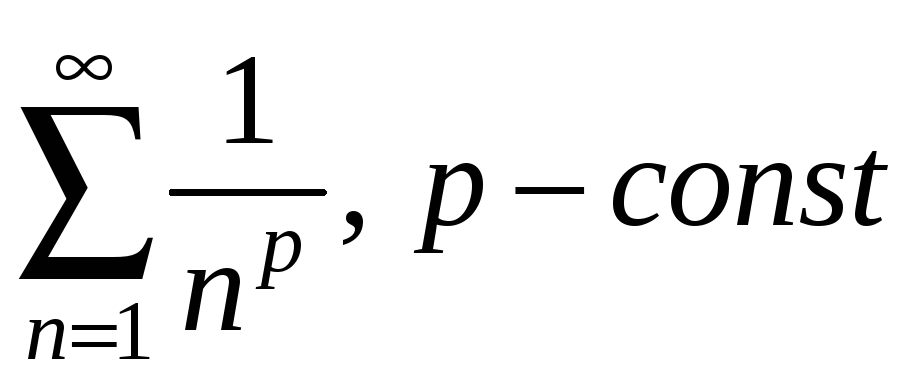 .
.
Розв’язання.
Цей ряд називають узагальненим гармонічним
рядом, а у випадку
![]() - просто гармонічним рядом.
- просто гармонічним рядом.
За
інтегральною ознакою, питання про його
збіжність вирішується за допомогою
невластивого інтеграла
![]() .
Який було розглянуто в §12 розділу
.
Який було розглянуто в §12 розділу
![]() .
Оскільки цей інтеграл збігається при
.
Оскільки цей інтеграл збігається при
![]() і розбігається при
і розбігається при
![]() ,
то і ряд
,
то і ряд
![]() збігається у випадку
збігається у випадку
![]() і розбігається при
і розбігається при
![]() .
.
Теорема
3.9
(перша ознака порівняння). Нехай для
рядів
![]() і
і
![]() виконано нерівність
виконано нерівність
![]() .
Тоді із збіжності ряду
.
Тоді із збіжності ряду
![]() випливає збіжність ряду
випливає збіжність ряду
![]() .
Якщо ряд
.
Якщо ряд
![]() розбігається, то і ряд
розбігається, то і ряд
![]() також
розбігається.
також
розбігається.
Доведення.
Введемо позначення
![]() ,
,
![]() .
Очевидно,
.
Очевидно,
![]() .
Якщо ряд
.
Якщо ряд
![]() збігається, то послідовність
збігається, то послідовність
![]() обмежена зверху, тоді послідовність
обмежена зверху, тоді послідовність
![]() також обмежена зверху. Отже, ряд
також обмежена зверху. Отже, ряд
![]() також збігається. Нехай ряд
також збігається. Нехай ряд
![]() розбігається, тоді ряд
розбігається, тоді ряд
![]() збігається не може. Адже у цьому випадку
(за доведеним вище) збігався б і ряд
збігається не може. Адже у цьому випадку
(за доведеним вище) збігався б і ряд
![]() .
.
Приклади. Дослідити збіжність рядів:
1)
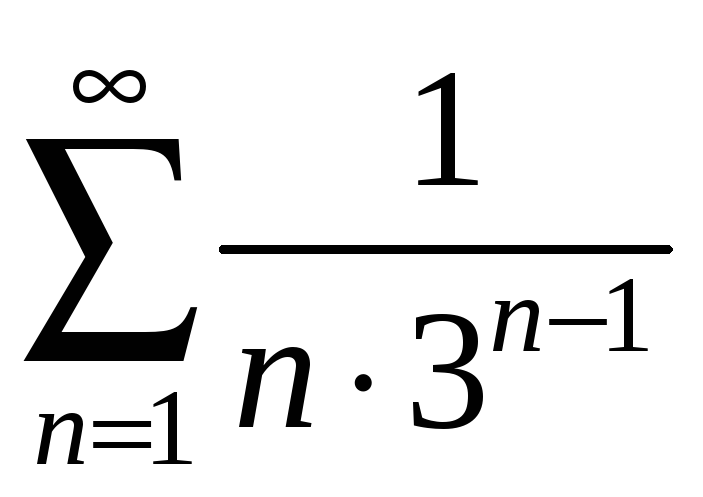 .
.
Розв’язання.
Оскільки
![]() ,
а геометричний ряд
,
а геометричний ряд
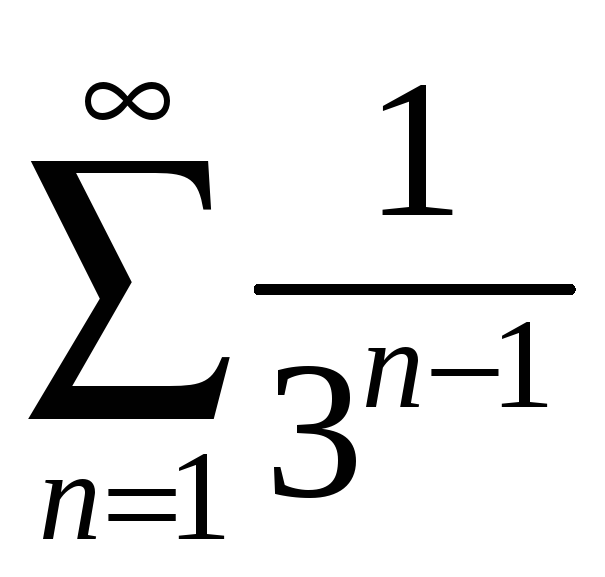
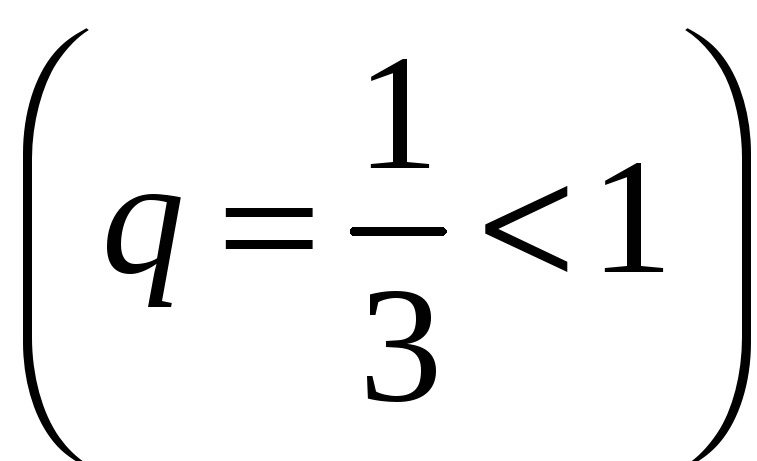 збігається, то збігається і ряд
збігається, то збігається і ряд
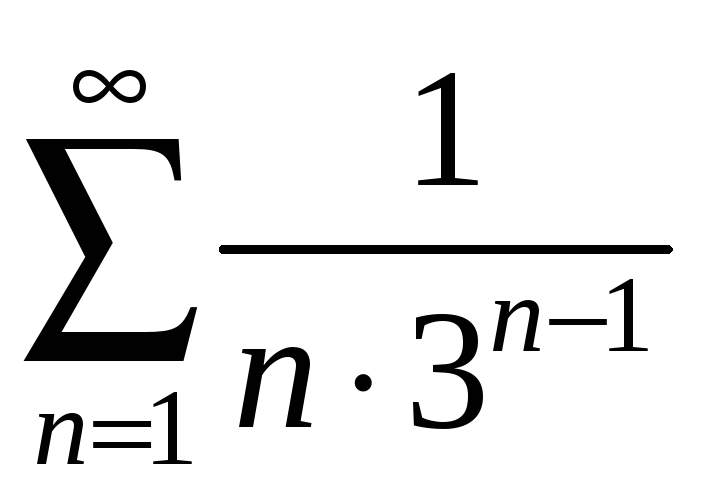 .
.
2)
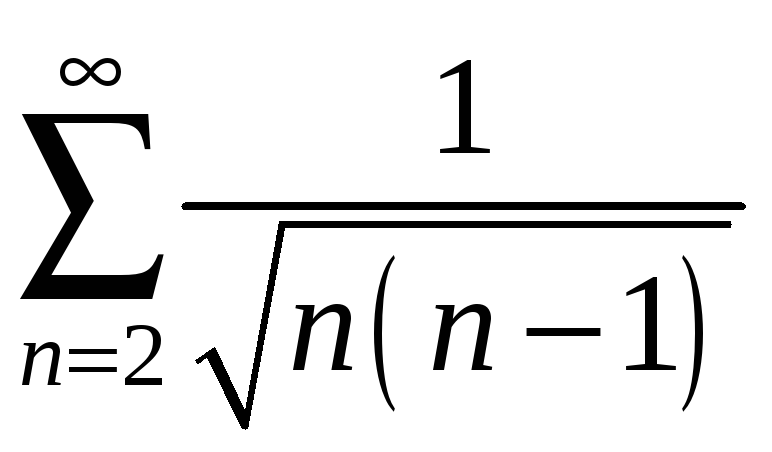 .
.
Розв’язання.
Очевидно, що
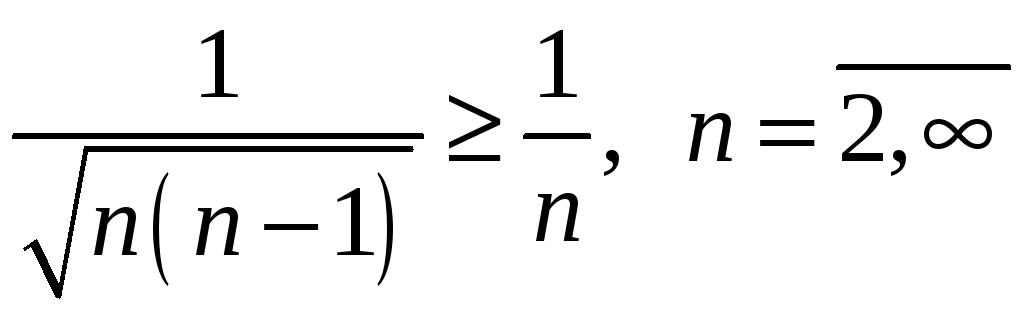 .
Гармонічний ряд
.
Гармонічний ряд
![]() розбігається, тому розбігається і ряд
розбігається, тому розбігається і ряд
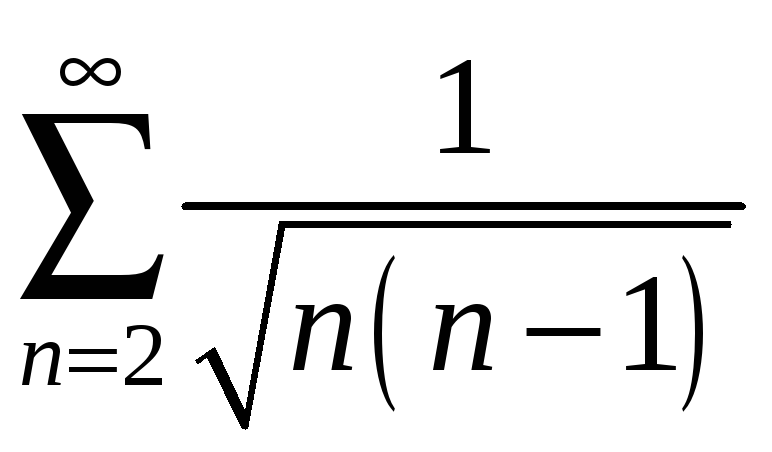 .
.
Зауваження.
Теорема 3.9 справедлива і в тому випадку,
коли нерівність
![]() виконується не для всіх
виконується не для всіх
![]() ,
а починаючи з деякого номера
,
а починаючи з деякого номера
![]() ,
тобто
,
тобто
![]() .
Адже відкидання декількох перших членів
ряду не впливає на його збіжність.
.
Адже відкидання декількох перших членів
ряду не впливає на його збіжність.
Теорема
3.10
(друга ознака порівняння) Якщо ряди з
додатними членами
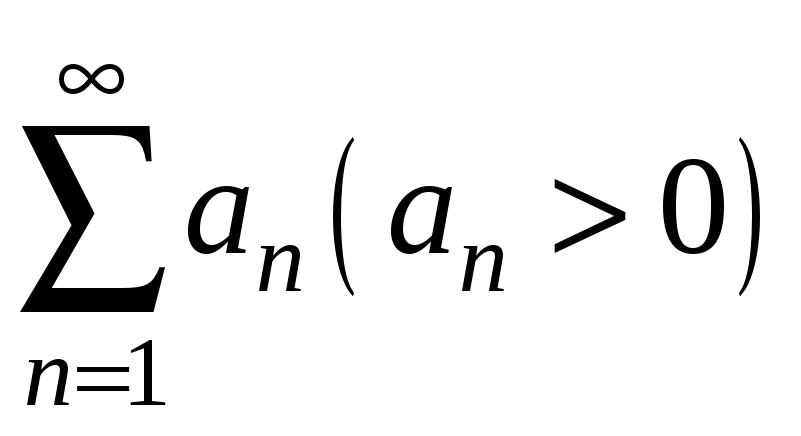 і
і
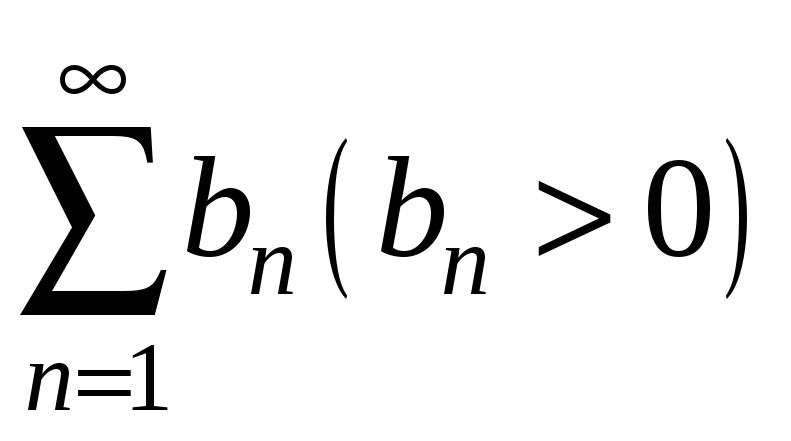 такі, що існує скінченна границя
такі, що існує скінченна границя
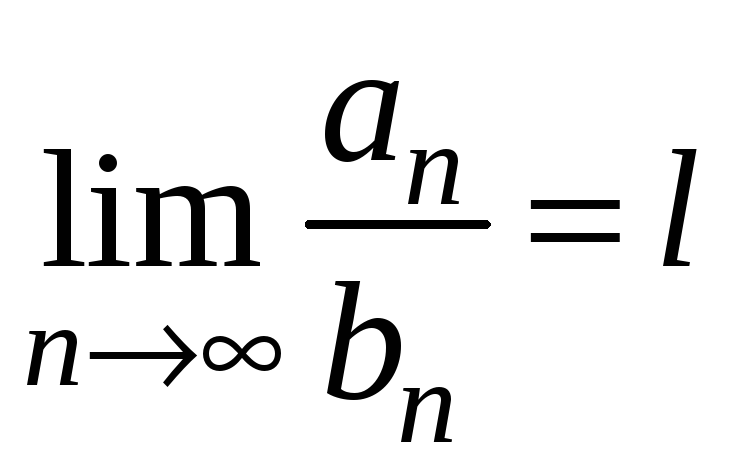
![]() ,
то ряди збігаються або розбігаються
одночасно.
,
то ряди збігаються або розбігаються
одночасно.
Доведення.
Те, що
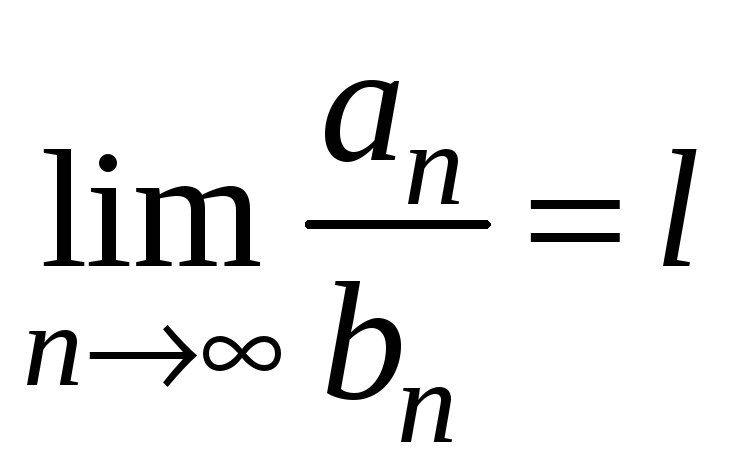 означає, що для будь-якого числа
означає, що для будь-якого числа
![]()
![]() знайдеться такий номер
знайдеться такий номер
![]() ,
що для всіх
,
що для всіх
![]() виконано нерівність
виконано нерівність
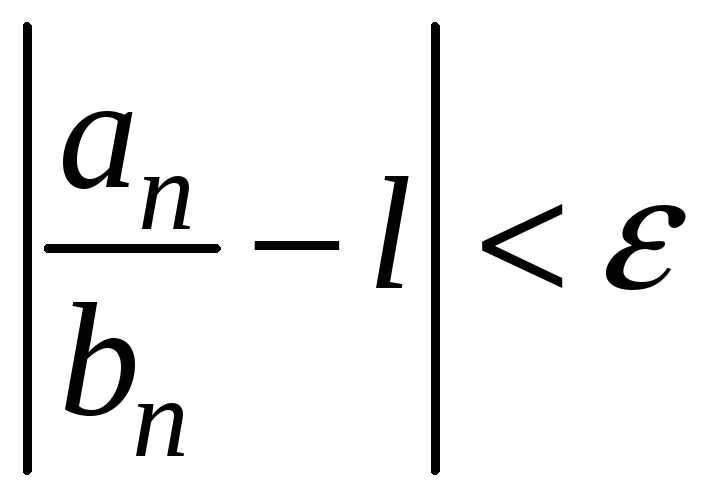 .
Тоді
.
Тоді
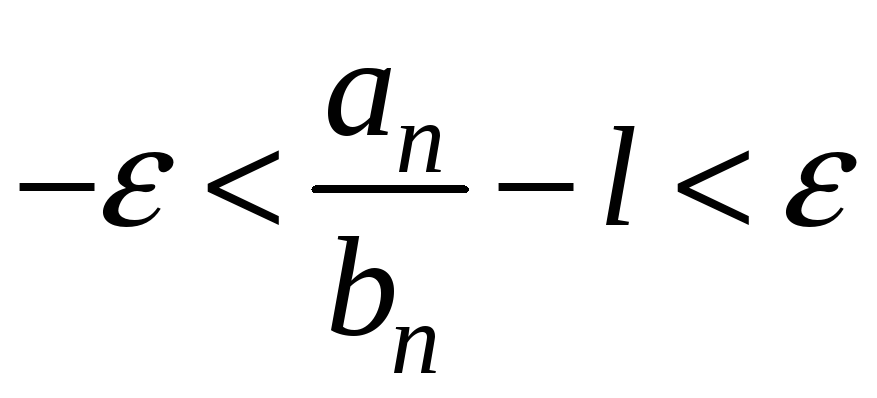 ;
;
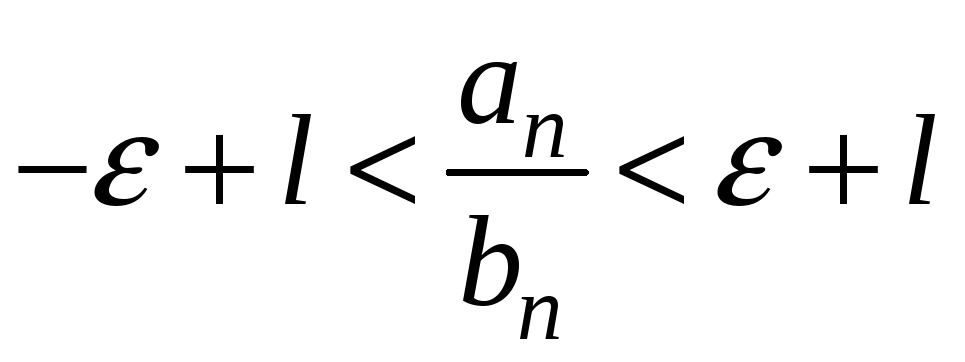 ;
;
![]() .
Якщо ряд
.
Якщо ряд
![]() збігається, то за теоремою 3.2 збігається
і ряд
збігається, то за теоремою 3.2 збігається
і ряд
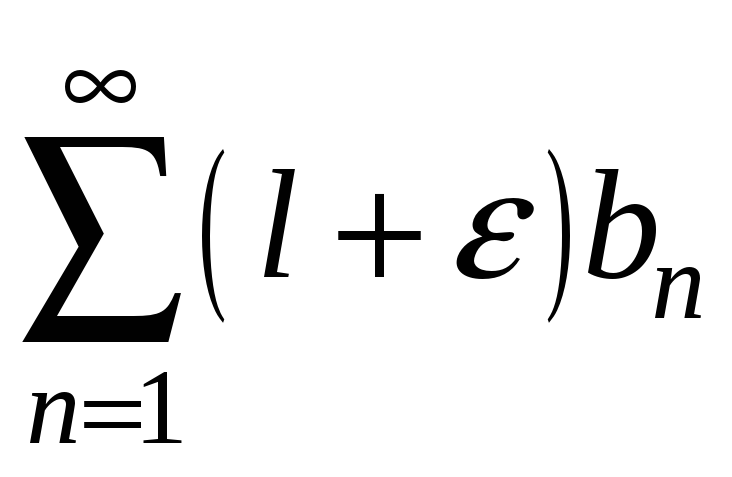 .
Тоді за теоремою 3.9 збігається і ряд
.
Тоді за теоремою 3.9 збігається і ряд![]() .
Нехай збігається ряд
.
Нехай збігається ряд
![]() ,
тоді з нерівності
,
тоді з нерівності
![]() (
(![]() вважаємо настільки малим, що
вважаємо настільки малим, що
![]() )
випливає, що ряд
)
випливає, що ряд
![]() збігається.
збігається.
Нехай
будь-який з рядів
![]() і
і
![]() розбігається, тоді за доведеним вище
другий ряд збігатись не може, адже в
цьому випадку збігався б і перший.
розбігається, тоді за доведеним вище
другий ряд збігатись не може, адже в
цьому випадку збігався б і перший.
Приклад.
Дослідити
збіжність ряду
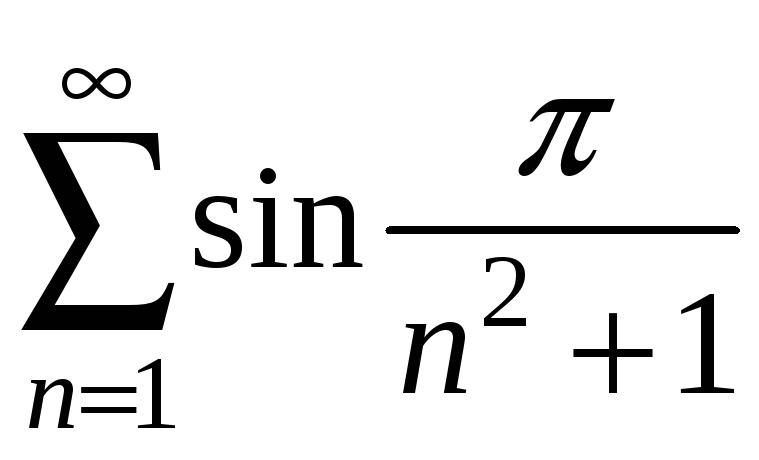 .
.
Розв’язання.
Розглянемо
збіжний ряд
![]() (
див. узагальнений гармонічний ряд,
(
див. узагальнений гармонічний ряд,
![]() ).
Обчислимо границю
).
Обчислимо границю
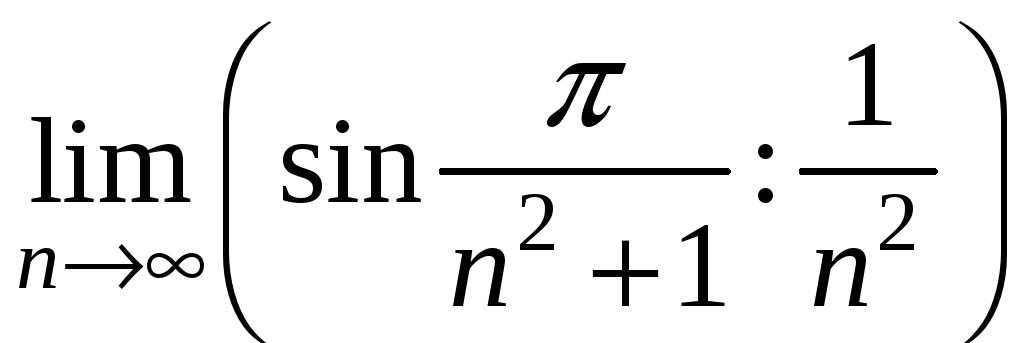 ,
замінивши нескінченно малу величину
,
замінивши нескінченно малу величину
![]() на еквівалентну їй
на еквівалентну їй
![]() .
Тоді
.
Тоді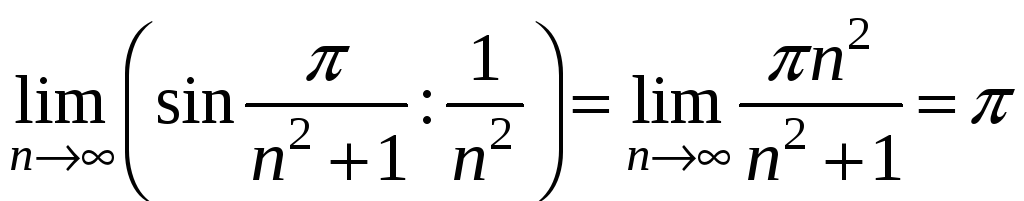 .
За теоремою 3.10 досліджуваний ряд поводить
себе так само, як і ряд
.
За теоремою 3.10 досліджуваний ряд поводить
себе так само, як і ряд
![]() ,
тобто збігається.
,
тобто збігається.
Теорема
3.11 (ознака
Даламбера) Нехай ряд з додатними членами
(3.2) такий, що існує (скінченна або
нескінченна границя)
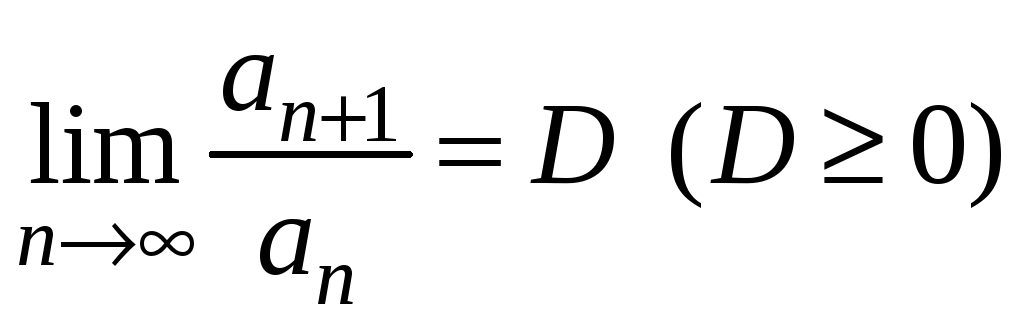 .
Тоді при
.
Тоді при
![]() ряд збігається, при
ряд збігається, при
![]() -
розбігається.
-
розбігається.
Доведення.
З означення границі маємо: для будь-якого
числа
![]() знайдеться такий номер
знайдеться такий номер
![]() ,
що
,
що
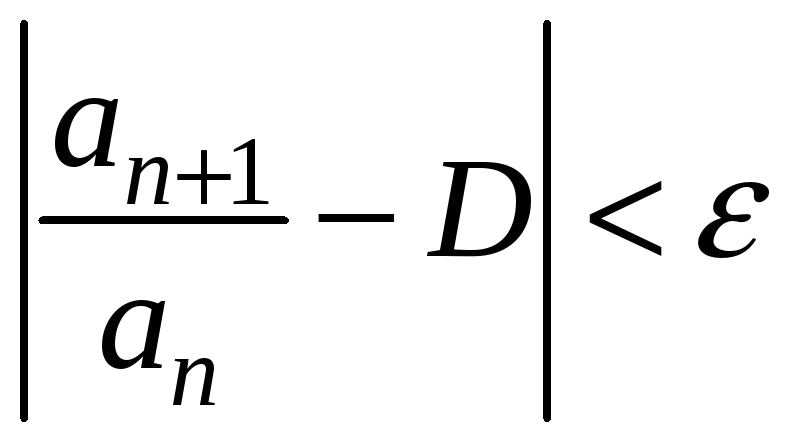 при
при
![]() .
Тоді
.
Тоді
![]() .
.
![]()
Позначимо
через
![]() .
Нехай
.
Нехай
![]() ,
,
![]() будемо вважати таким малим, що
будемо вважати таким малим, що
![]() .
Тоді
.
Тоді
![]() ,
тобто
,
тобто
![]() ;
;
![]() ;
;
![]() .
.
Це
означає, що члени ряду
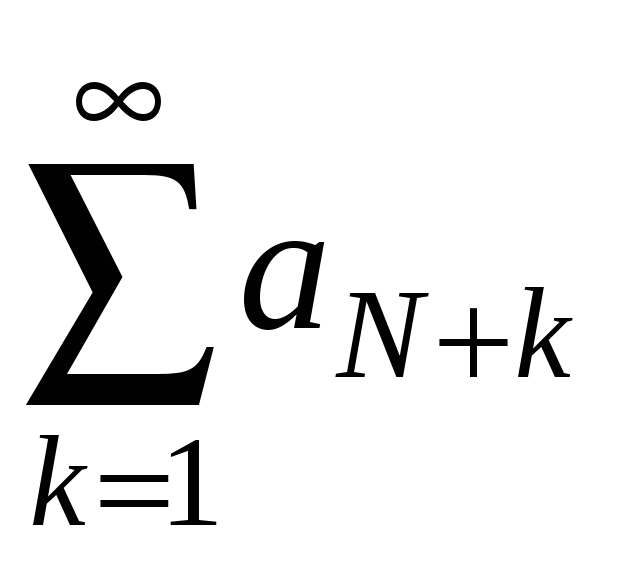 (залишку ряду
(залишку ряду
![]() )
менші за відповідні члени геометричного
ряду
)
менші за відповідні члени геометричного
ряду
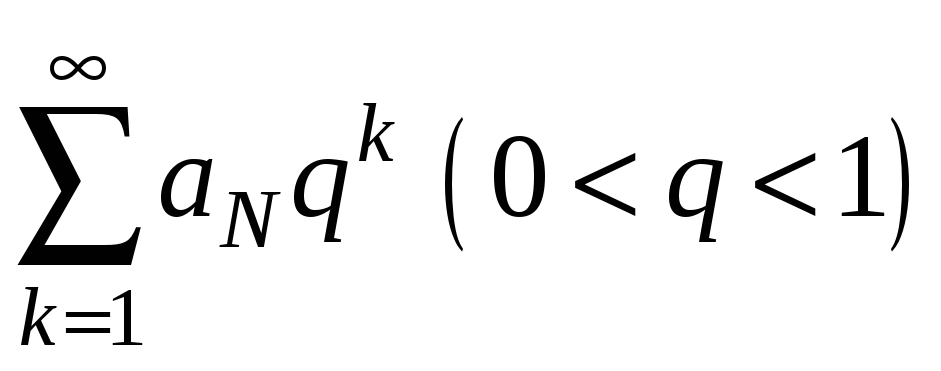 ,
який збігається. За теоремою порівняння
збігається і ряд
,
який збігається. За теоремою порівняння
збігається і ряд
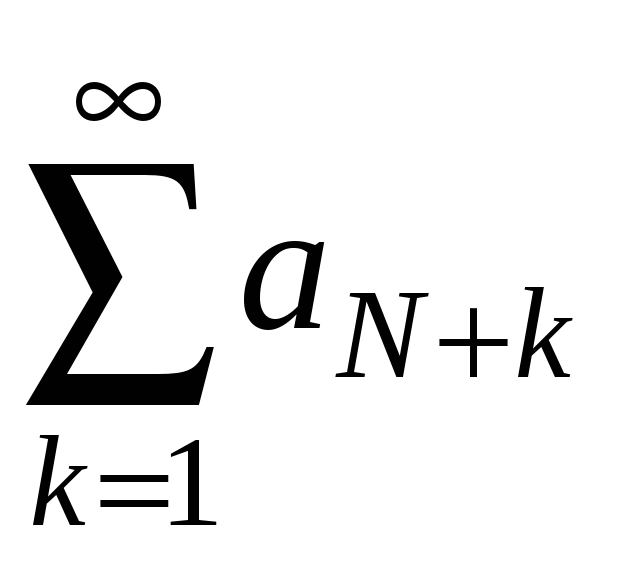 .
Тоді і ряд
.
Тоді і ряд
![]() також збігається.
також збігається.
Нехай
![]() ,
,
![]() візьмемо настільки мале, що
візьмемо настільки мале, що
![]() .
Тоді з нерівності (3.5) маємо:
.
Тоді з нерівності (3.5) маємо:
![]() .
Таким чином, члени ряду
.
Таким чином, члени ряду
![]() після
після
![]() - ного члену зростають при зростанні
номеру
- ного члену зростають при зростанні
номеру
![]() .
Це означає, що
.
Це означає, що
![]() .
Отже ряд розбігається.
.
Отже ряд розбігається.
Приклад.
Дослідити
збіжність ряду
![]() .
.
Розв’язання.
Загальний
член ряду
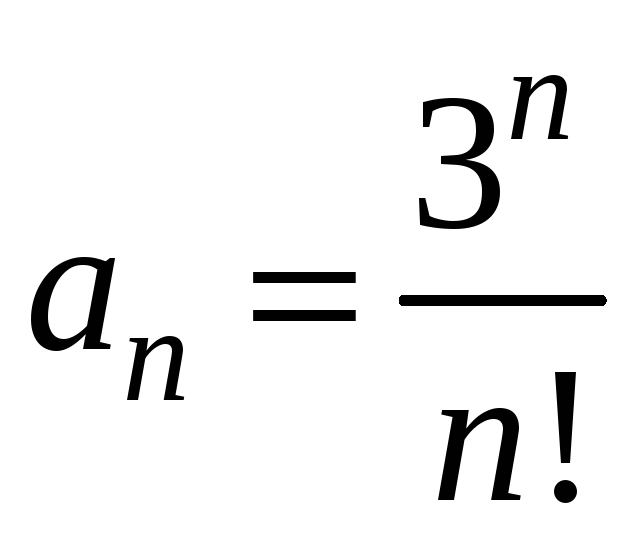 ,
тоді наступний член
,
тоді наступний член
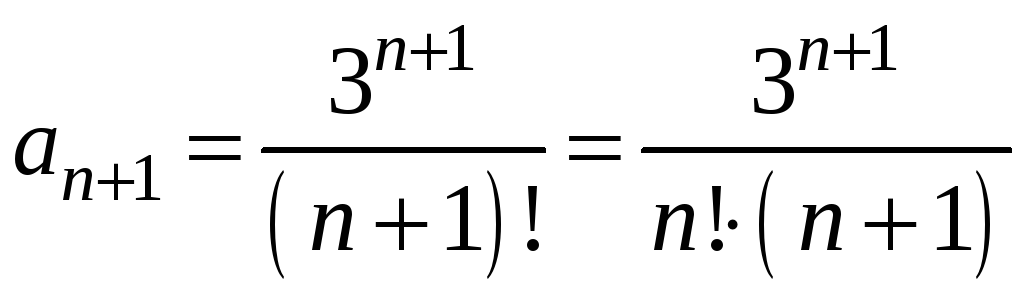 .
Тоді
.
Тоді
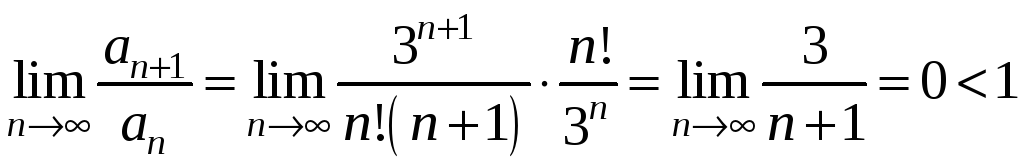 .
Отже ряд збігається.
.
Отже ряд збігається.
Теорема
3.12 (ознака
Коші коренева). Нехай ряд з додатними
членами
![]()
![]() такий, що існує границя
такий, що існує границя
![]() (скінченна або нескінченна). Тоді при
(скінченна або нескінченна). Тоді при
![]() ряд збігається, а при
ряд збігається, а при
![]() - розбігається. Пропонуємо довести цю
теорему самостійно по аналогії з
доведенням ознаки Даламбера.
- розбігається. Пропонуємо довести цю
теорему самостійно по аналогії з
доведенням ознаки Даламбера.
Теорема
3.13 Якщо
ряд
![]()
![]() ,
збігається, і його сума дорівнює
,
збігається, і його сума дорівнює
![]() ,
то ту ж саму суму має ряд отриманий
будь-якою перестановкою його членів.
,
то ту ж саму суму має ряд отриманий
будь-якою перестановкою його членів.
Доведення.
Нехай
![]() -
-
![]() - на часткова сума ряду
- на часткова сума ряду
![]() .
Переставимо якимось чином його члени
і знайдемо суму перших
.
Переставимо якимось чином його члени
і знайдемо суму перших
![]() членів отриманого ряду:
членів отриманого ряду:
![]() .
Позначимо через
.
Позначимо через
![]() найбільший з номерів
найбільший з номерів
![]() .
Тоді
.
Тоді
![]() .
Тобто послідовність часткових сум
отриманого ряду
.
Тобто послідовність часткових сум
отриманого ряду
![]() обмежена зверху. Отже ряд збігається,
і його сума
обмежена зверху. Отже ряд збігається,
і його сума
![]() задовольняє нерівність
задовольняє нерівність
![]() .
Таким чином, сума
.
Таким чином, сума
![]() ряду, отриманого перестановкою членів
ряду
ряду, отриманого перестановкою членів
ряду
![]()
![]() не може бути більшою за
не може бути більшою за
![]() .
Але ж вона не може буди і меншою. Адже
після зворотної перестановки ми отримаємо
ряд
.
Але ж вона не може буди і меншою. Адже
після зворотної перестановки ми отримаємо
ряд
![]() ,
сума якого
,
сума якого
![]() має задовольняти нерівність
має задовольняти нерівність
![]() .
Таким чином
.
Таким чином
![]() .
Теорему доведено.
.
Теорему доведено.
