Теорема умножения вероятностей зависимых событий

Вероятность совместного появления двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

№37

Событие В называют независимым от события А,если появление события

А не изменяет вероятности событияВ, т. е. если условная вероятность событияВ равна его безусловной вероятности:

РА(В) =Р (В).

Для независимых событий теорема умножения

Р (АВ) =Р (А)РА (В)

имеет вид

Р (АВ) =Р(А)Р (В),

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Два события называют независимыми,если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.

№38

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны.

Теорема. Вероятность появления хотя бы одного из событийА1,А2, …,Аnнезависимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событийA1 ,A2 , …,An :

P(A)=1-q1q2 …qп .

Замечание. Если событияА1,А2, …,Аn имеют одинаковую вероятность, равнуюр, то вероятность появления хотя бы одного из этих событий

P(A)=1-qп .

№39

Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:Р(А+В) =Р(А)+Р(В)-Р(АВ).

№40

Теорема. Вероятность событияА, которое может ступить лишь при условии появления одного из несовместных событийB1, В2, ...,Вп, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:Р(А)=Р(В1)PB,

A +Р(В2)PB A +…+Р(Вп)PBn AЭту формулу называют «формулой полной вероятности».

Если событие А уже произошло, для нахождения так называемой переоценённой вероятности гипотез применяется формула Байеса:

№41

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p(0<p<1),событие наступит ровно r раз (безразлично, в какой последовательности), равна

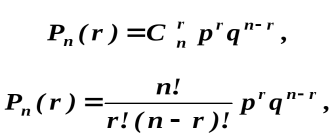
где q=1-p.

Вероятность того, что событие наступит: а) менее r раз; б) более r раз; в) не менее r раз; г) не более r раз – находят соответственно по формулам:

а) P_n(0)+P_n(1)+…+P_n(r-1);

б) P_n(r+1)+P_n(r+2)+…+P_n(n);

в) P_n(r)+P_n(r+1)+…+P_n(n);

г) P_n(0)+P_n(1)+…+P_n(r).

Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то пользуются приближенной формулой,

где k – число появления события в n независимых испытаниях, =np (среднее число появления события в n испытаниях) и говорят, что случайная величина распределена по закону Пуассона.

Пример 29. Вероятность рождения мальчика 0.515. В семье 6 детей. Найти вероятность того, что из них:

а) ровно три девочки,б) не более трех девочек,в) не менее двух, но не более четырех девочек.

№42

Локальная теорема Лапласа

Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится виспытаниях ровнораз приближённо определяется по формуле

при .

Интегральная теорема Лапласа

Если вероятность р наступления события А в каждом испытании постоянна, отлична от нуля и единицы, то вероятность  того, что событие А появится в испытаниях отдораз, приближённо равна определённому интегралу

,где  

№43

Определение. Дискретной называется случайная величина , множество возможных значений которой конечнолибо счетно, то есть перенумерованное бесконечное.

Определение. Законом распределения дискретной случайной величины называется соответствие между возможными значениями случайной величины и соответствующими вероятностями.

Простейшей формой задания закона распределения дискретной случайной величины является таблица, в первой строке которой находятся все возможные значения случайной величины, а во второй – соответствующие им вероятности:

X	xl	х2	. . . хп
Р	р1	р2	рп

Определение. Табличное представление закона распределения дискретной случайной величины называется рядом распределения.

Для наглядности прибегают к графическому изображению ряда распределения: по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат – соответствующие вероятности. Полученные точки соединяют отрезками прямых. Такая фигура называется многоугольником распределения.

№44

Необходимо найти закон распределения величины X. Для этого требуется определить возможные значенияX и их вероятности. Очевидно, событиеА вп испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, . .

. , либо п раз. Таким образом, возможные значенияX таковы:х1 = 0,x 2 = l ,x3 = 2,. . . ,хп+1 = п. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли (1.4). Она и является аналитическим выражением искомого закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли.

Напишем биномиальный закон в виде таблицы:

X n	n-1	. . .	k	. . . 0
Ррп	прп-1q . . .Ckn рkqn-k . . .			qn.

Отклонением называют разность между случайной величиной и ее математическим ожиданиям.

Приведем важное свойство отклонения.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина X может принимать только значенияxl, х2, . . .,хп, вероятности которых соответственно равныр1,р2,. . .,рп.. Тогда математическое ожиданиеМ (X) случайной величиныX определяется равенством

М (X) =х1 р1 +х2 р2 + . . . +хп рп.

Теорема. Математическое ожидание отклонения равно нулю:

М [X - М(Х)]=0.

Дисперсией (рассеянием) дискретной случайной величины называют ма-

тематическое ожидание квадрата отклонения случайной величины отее мате-

25

матического ожидания:

D(X)=M[Х-M(X)]2.

Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величиныХ и квадратом ее математического ожидания:

D(X)=M(X2)-[M(X)]2.

Средним квадратическим отклонением случайной величины Хназыва-

ют квадратный корень из дисперсии:

X D X.

Размерность X совпадает с размерностьюХ, поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют средне квадратическое отклонение, а не дисперсию.

№45

1. Математическое ожидание постоянной величины равно самой постоянной, т.е. М(С)=С.

Доказательство. Постоянную величину можно рассматривать как дискретную с одним значением х₁=С и вероятностью этого значения р₁=1. По формуле (6.1) получим М(С)=С∙1=С.

Свойство доказано.

2. Математическое ожидание алгебраической суммы двух случайных величин равно алгебраической сумме их математических ожиданий, т.е. М(Х±Y) = М(Х) ± М (Y).

Доказательство. Доказательство проведем только для дискретных случайных величин. Пусть случайные величины Х и Y заданы своими рядами распределения:

Х	x1	x2	…	xn	и	Y	y1	y2	…	ym
P	p1	p2	…	pn	Q	q1	q2	…	qm

 

Возможными значениями суммы Х±Y являются числа х_i ± у_j. Обозначим через p_ij вероятность того, что величина X примет значение х_i, а величина Y примет значение у_j. По определению математического ожидания имеем .

Нетрудно понять, что по теореме о полной вероятности имеют место равенства  . Следовательно, .

Свойство доказано.