№1

Числовые ряды – рассмотрим числовую последовательность: u_n – числа.

Составим суммы: ;

;

;

Выражение:  – называется числовым рядом (1)

Числа  - называются членами ряда. Если они положительны, то ряд называется знакоположительным.

Ряд геометрической прогрессии – Исследуем на сходимость ряд: Этот ряд называется рядом (2) геометрической прогрессии.

№2

Простейшие свойства числовых рядов:

1)Если ряд сходиться к сумме S, то сходиться и ряд к сумме aS, где a-число.

2)Если сходиться, то сходиться aряд составленный из суммы и разности членов этих рядов S=S1+S2

3)Если сходиться U1+U2….Uk+Uk+1+……Un+Un+1…., то сходиться и ряд Uk+1+Uk+2+…….Un+Un+1+…

Необходимый признак сходимости ряда:

Если ряд  сходится, то его общий член стремится к нулю при, т.е. .

№3

Признак сравнения

Пусть и– знакоположительные ряды. Если для всехвыполняется неравенство, то из сходимости рядаследует сходимость ряда, а из расходимости рядаследует расходимость ряда.

Предельный признак сравнения

Пусть и– знакоположительные ряды. Если существуетконечный и не равный нулю предел , то оба рядаи

одновременно сходятся или одновременно расходятся.

Признак Даламбера

Пусть – знакоположительный ряд. Если существует , то при ряд сходится, а при ряд расходится.

Если , то признак Даламбера не дает возможности судить о поведении ряда. В этом случае необходимо дополнительное исследование, например, с помощью признаков сравнения.

Радикальный признак Коши

Пусть – знакоположительный ряд. Если существует ,

то при ряд сходится, а при ряд расходится.

Если ряд может как сходиться, так и расходиться. Выяснить это можно с помощью дополнительного исследования, например, используя признаки сравнения.

Интегральный признак Коши

Пусть члены знакоположительного ряда не возрастают:

. Пусть, кроме того, – непрерывная,

невозрастающая функция, определенная для всех , такая, что

. Тогда ряд и несобст-

венный интеграл сходятся или расходятся одновременно.

№4

Знакопеременные ряды

Знакопеременными называются ряды, члены которых могут иметь любые знаки, например, .

В частности, если положительные и отрицательные члены ряда следуют друг за другом поочередно, то такой знакопеременный ряд называется знакочередующимся.

Знакочередующие ряды

Знакочередующий ряд, члены которого являются положительными, можно представить в виде

,

где 

Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

Признак Лейбница

Для знакочередующихся рядом действует достаточный признак сходимости Лейбница.

Пусть {an} является числовой последовательностью, такой, что

1. an+1 <an для всех n;

2. 

Тогда знакочередующиеся ряды и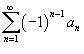сходятся

Абсолютная и условная сходимость

Ряд называется абсолютно сходящимся, если ряд также сходится.

Если ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.

Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

№5

Функциональным рядом называется ряд

,

членами которого являются функции одного и того же аргумента, определенные на одном множестве Е.

Степенным рядом называется функциональный ряд

 (21)

члены которого являются произведениями постоянных C₀ , C₁ , ... , C_n ,... на степенные функции от разности x-x₀ с целыми неотрицательными показателями степеней, точка x₀ называется центром степенного ряда.

Опираясь на теорему Абеля можно доказать, что существует такое положительное число R, что для всех x, удовлетворяющих неравенству |x-x₀|<R, ряд сходится абсолютно и расходится при всех x, для которых |x-x₀|>R.

Число R называется радиусом сходимости ряда , а интервал (x₀-R, x₀-R) – интервалом сходимости.

№6

Первый способ. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда : . Применим признак Даламбера:

.

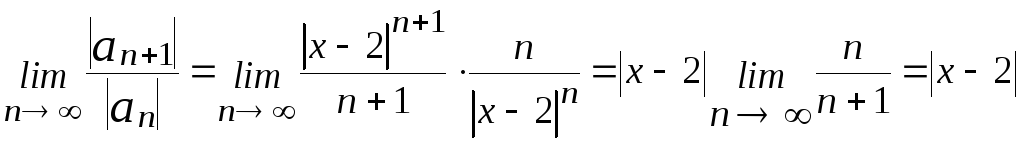Если |x-2|<1, то ряд сходится. Итак, -1<x-2<1, 1<x<3 – интервал сходимости данного ряда. Поведение данного ряда на концах интервала сходимости, т.е. в точках x=1 и x=3, исследуется отдельно.

При x=1 из данного ряда получаем ряд , который условно сходится.

При x=3 получаем гармонический ряд  , который расходится.

Итак, данный ряд сходится абсолютно при 1<x<3 и условно при .x=1.

Второй способ решения. Если для степенного ряда (2) существует , то радиус сходимости степенного ряда можно вычислить по формуле. (22)или

В нашем случае  и , поэтому . Так как x₀=2 – центр степенного ряда, то (x₀-R, x₀+R)=(1;3) – интервал сходимости данного ряда.

Сходимость ряда на концах интервала сходимости исследована выше.

Итак, данный ряд сходится абсолютно при 1<x<3 и условно при х=1.

№7

Свойство 1. Функция является непрерывной на любом отрезке , принадлежащем интервалу сходимости.

Свойство 2. Функция дифференцируема на интервале , и ее производная может быть найдена почленным дифференцированием ряда (1.2), т. е.

,для всех .

Свойство 3. Неопределенный интеграл от функции для всех может быть получен почленным интегрированием ряда (1.2), т. е.

для всех .

Следует отметить, что при почленном дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость на концах интервала может измениться.

№8

№16

Алгебраической формой комплексного числа называется запись комплексного числа  в виде z=x+iy , где  и  – действительные числа,  – мнимая единица, удовлетворяющая соотношению i^2=-1 .

Число x называется действительной частью комплексного числа z и имеет обозначение x=Rez .

Число y называется мнимой частью комплексного числа z и имеет обозначение y=Imz .

Сравнение

Два комплексных числа z1=x1+iy1 и z2=x2+iy2 называются равными, если x1=x2,y1=y2, т.е. равны их действительные и мнимые части.

Сложение

Сложение комплексных чисел z1=x1+iy1 и z2=x2+iy2 выполняется непосредственным суммированием действительных и мнимых частей: z1+z2=(x1+x2)+i(y1+y2)

Вычитание

Вычитание комплексных чисел z1=x1+iy1  и z2=x2+iy2   выполняется непосредственным вычитанием действительных и мнимых частей: z1-z2=(x1-x2)+i(y1-y2)

Умножение

Умножение комплексных чисел z1=x1+iy1   и z2=x2+iy2    выполняется непосредственным произведением чисел в алгебраической форме, учитывая свойство мнимой единицы i^2=-1:

Z1*Z2=(x1*x2-y1*y2)+i(x1*y2+x2*y1)

3) Деление комплексных чисел

Для того чтобы выполнить деление комплексных чисел, надо числитель и знаменатель умножить на комплексное число, сопряженное знаменателю:

Следовательно,

№17

Тригонометрическая форма комплексного числа

r = sqrt(a²+ b²) cosf = a/r        a = r*cosf sinf = b/r        b = r*sinf

a + bi = r*(cosf + isinf) Число r - модуль комплексного числа. f - аргумент комплексного числа (argZ, Z = a + bi) Аргумент Z определяется с точностью до слагаемого равного 2*pi и может быть как положительным так и отрицательным. Обычно главное значение argZ выбирается в промежутке [0, 2*pi]. Запись: Z = a + bi - алгебраическая форма. Запись: Z = r*(cosf + isinf) - тригонаметрическая форма.

Действия над комплексными числами в тригонометрической форме

Z₁ = r₁(cosf₁+ isinf₁) Z₂ = r₂(cosf₂+ isinf₂) Z₁*Z₂ = r₁(cosf₁ + isinf₁) * r₂(cosf₂+ isinf₂) = r₁*r₂[(cosf₁*cosf₂- sinf₁*sinf₂) + (cosf₁*sinf₂+ sinf₁*cosf₂)i] =  = r₁*r₂[cos(f₁+ f₂) + sin(f₁+ f₂)i] Z₁/Z₂ = [r₁(cosf₁+ isinf₁)] / [r₂(cosf₂+ isinf₂)] = (r₁/r₂) * [(cosf₁+ isinf₁) * (cosf₂- isinf₂) / (cos²f₂+ isin²f₂)] =  = (r₁/r₂) * [cos(f₁- f₂) + sin(f₁- f₂)i] Zⁿ = rⁿ(cosfn + isinfn) Z^1/n = r^1/n[cos((f + 2*pi*k)/n) + isin((f + 2*pi*k)/n)], k = 0, 1, ..., n-1

№18

  Действия над комплексными числами в показательной форме выполняются по правилам действий со степенями:

Запись комплексного числа z в виде z=r⋅eiφ называется показательной формой записи, где число r - модуль комплексного числа z, φ - аргумент комплексного числа.

№19

№20

1) Показательная функция (формула Эйлера).

2) Тригонометрические функции,,,.

3) Гиперболические функции,,,.

4) Логарифмическая функция

Главное значение(главная ветвь).

5. Степенная функция

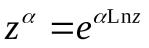
Главная ветвь.

6. Показательная функция

Главная ветвь.

7. Обратные тригонометрические функции Arcsinz,Arccosz,Arctgz…

Например,w=Arcsinz => z =sinw= (e^iw-e^-iw)/2ie^2iw –2ize^2iw-1=0

=Arcsinz

№21

предел отношения  =  , если  любым способом стремится к нулю.

Таким образом, .

Функция, имеющая производную при данном значении  , называется дифференцируемой (или моногенной) при этом значении  . Если функция  однозначна и имеет конечную производную в каждой точке области D, то эта функция называется аналитической в области D.

Если функция  дифференцируема в точке  , то в этой точке существуют частные производные  ,  ,  ,  , причем эти производные связаны условиями

 ,  ,

которые называются условиями Коши-Римана.

Условия Коши-Римана являются необходимыми условиями дифференцируемости функции  в точке  .

Обратно, если частные производные  ,  ,  ,  непрерывны в точке  и условия Коши-Римана  ,  выполнены, то функция  дифференцируема в точке  .

№22

Пусть функция  аналитична в точке  и .

Выясним геометрический смысл аргумента и модуля производной.

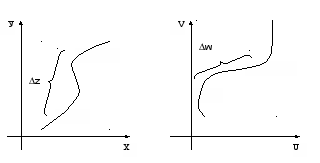
По определению 

т.е. модуль производной — это отношение бесконечно малого приращения (расстояния)  к бесконечно малому приращению аргумента (расстоянию) , кото­рое одинаково по всем направлениям .

№23

Пусть кривая l на плоскости Оху аргумента z при преобразовании переходит в кривую L на плоскости Оuv и при этом точка z0 переходит в точку w0. Тогда

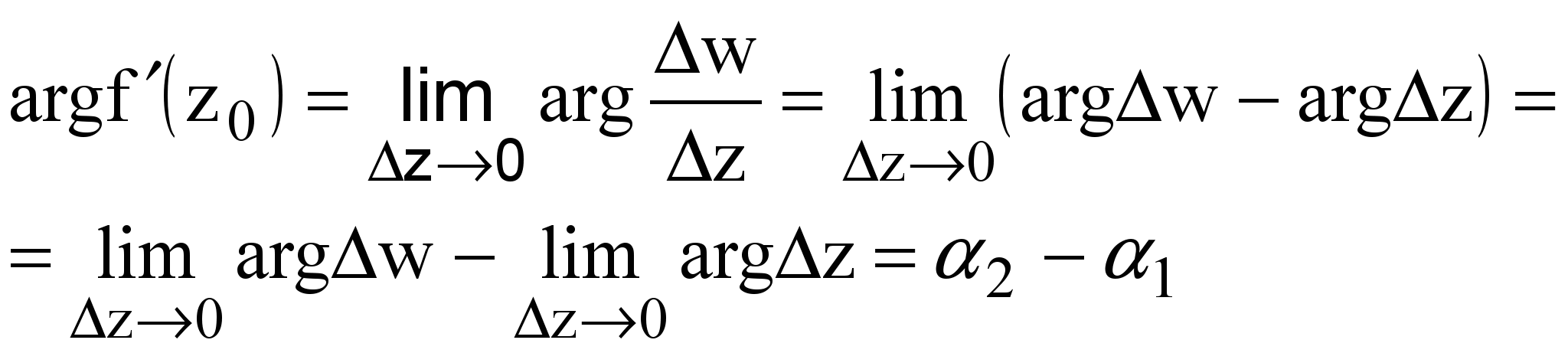
т.е.

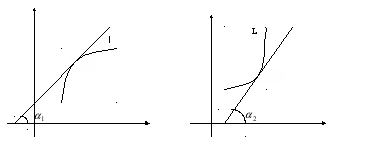
Итак, — это угол, на который надо повернуть касательную к кривой  в точке , чтобы получить направление касательной к кривой  в точке w0.

По определению 

т.е. модуль производной — это отношение бесконечно малого приращения (расстояния)  к бесконечно малому приращению аргумента (расстоянию) , кото­рое одинаково по всем направлениям .

Таким образом, геометрический смысл модуля производной состоит в том, что величина  определяет коэффициент растяжения (подобия) в точке при отображении .

Величину  при называется коэффициентом растяжения, а при — сжатия.

№31

Наблюдаемые нами события можно подразделить на три вида: досто-

верные, невозможные, случайные.

Достоверным называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условийS. Например, если в сосуде содержится вода при нормальном атмосферном давлении и температуре 200 (совокупность условийS), то событие «вода в сосуде находится в жидком состоянии» есть достоверное.

Невозможным называется событие, которое заведомо не произойдет, если будет осуществлена совокупность условийS. Например, событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет, если будет осуществлена совокупность условий предыдущего примера.

Случайным называют событие, которое при осуществлении совокупности условийS может либо произойти, либо не произойти. Например, брошенная монета может упасть либо «орлом», либо «решкой». Поэтому событие «при бросании монеты выпал «орел»» - случайное. 

События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Пример 2. Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» - несовместные.

№32

Вероятностью события а называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу