Занятие № 7 Распад, столкновение и рассеяние частиц

1. Система состоит из одной частицы с массой и частиц с одинаковыми массами . Исключить движение центра инерции и свести задачу к задаче о движении частиц.

2. Частица с массой испытала абсолютно упругое соударение с покоившейся частицей с массой 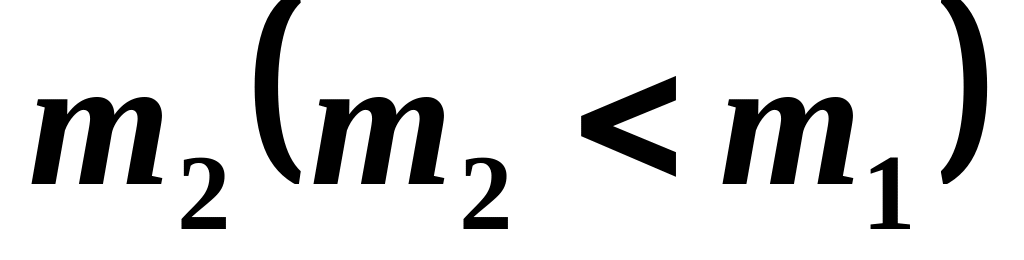. Найти максимальный угол, на который может отклониться в результате удара налетающая частица.

3. Молекула испытала соударение с покоившейся молекулой той же массы. Показать, что угол между направлениями разлета молекул после удара равен 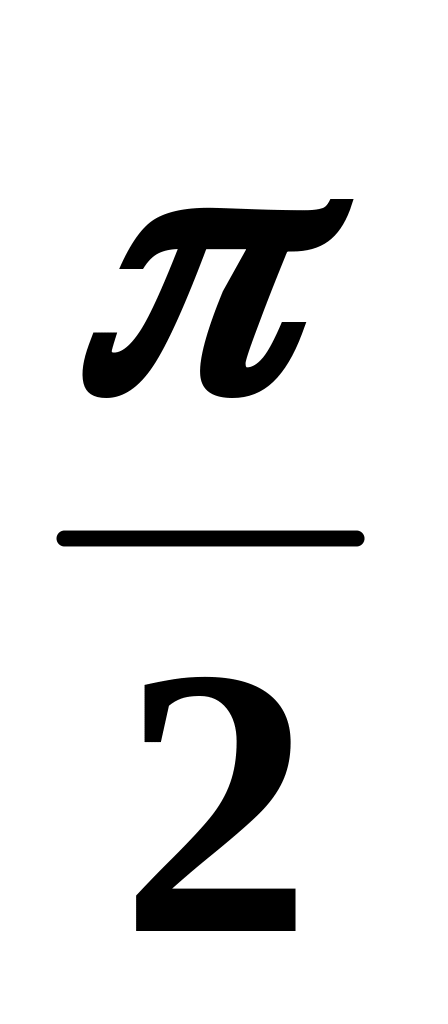, если соударение абсолютно упругое, и отличен от , если соударение неупругое.

4. Найти соотношение между углом рассеяния в системе центра инерции и углом рассеяния в системе координат, связанной с какой-либо из двух рассеивающихся частиц.

5. Найти в пространстве импульсов уравнения поверхностей, на которых лежат концы векторов импульсов рассеянных частиц.

Занятие № 8 Механические колебания

1. Частица массой движется по гладкой горизонтальной направляющей и соединена легкой пружиной жесткостью и длиной в ненапряженном состоянии с неподвижной точкой, находящейся на расстоянии от направляющей. Найти лагранжиан и частоту малых колебаний частицы.

2. Шарик массой может двигаться по гладкой параболе 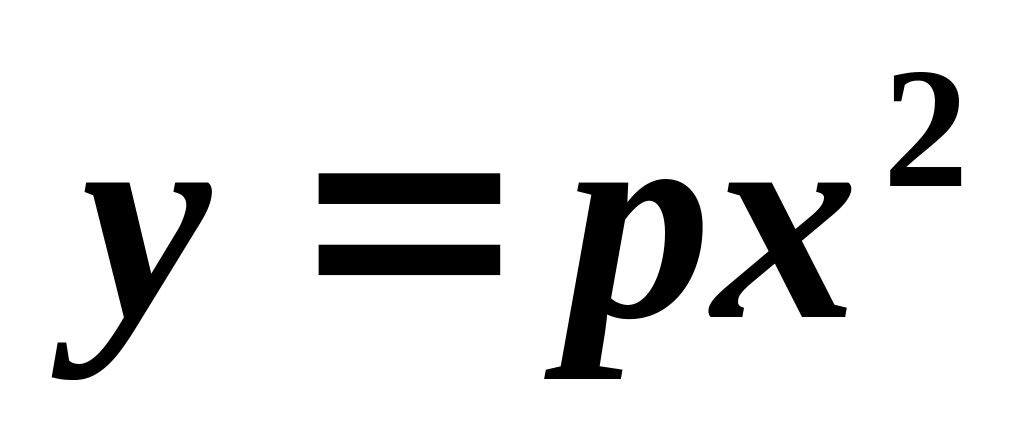с осью , направленной вертикально вверх. Шарик прикреплен к двум одинаковым легким пружинам с жесткостями , навитым на параболу и жестко закрепленным другими концами на одинаковых измеренных вдоль параболы расстояниях от ее вершины. Найти частоту малых колебаний шарика.

3. Составить уравнение движения математического маятника массой и длиной , точка подвеса которого движется по наклоненной под углом к горизонту прямой в плоскости качаний маятника по известному закону .

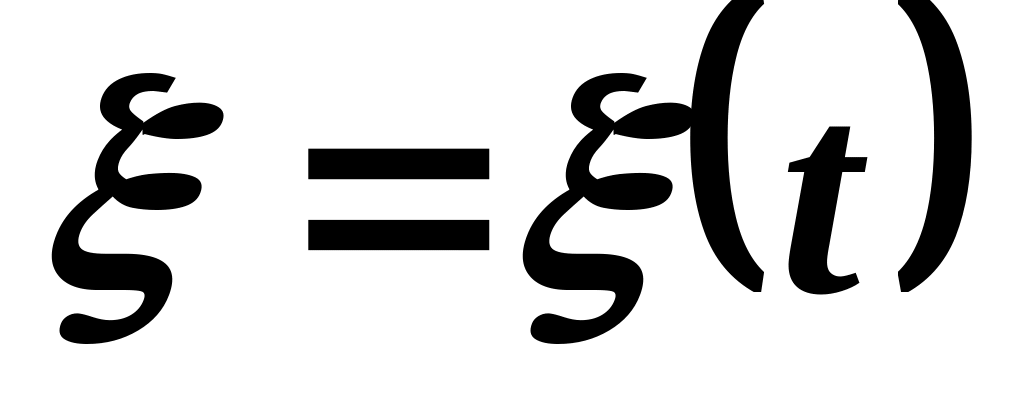4. Частица совершает затухающие колебания с частотой и коэффициентом затухания . Найти амплитуду скорости частицы как функцию времени, если в момент 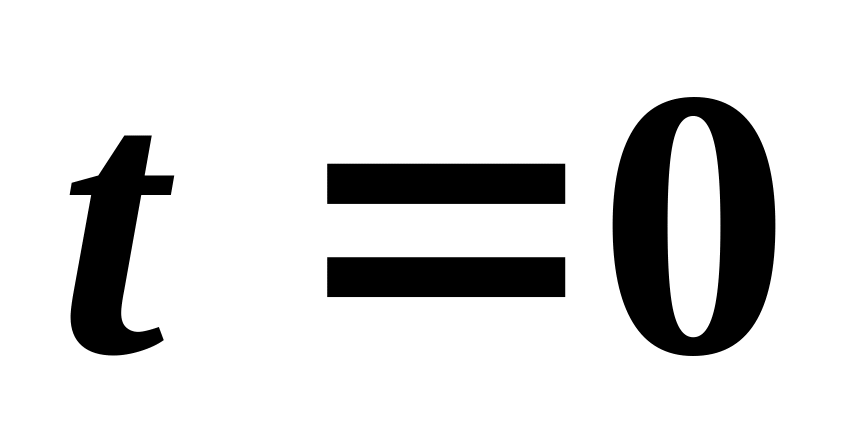: а) амплитуда смещения равна 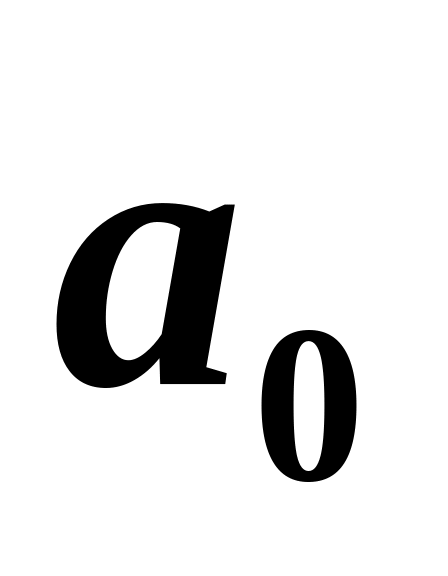; б) смещение 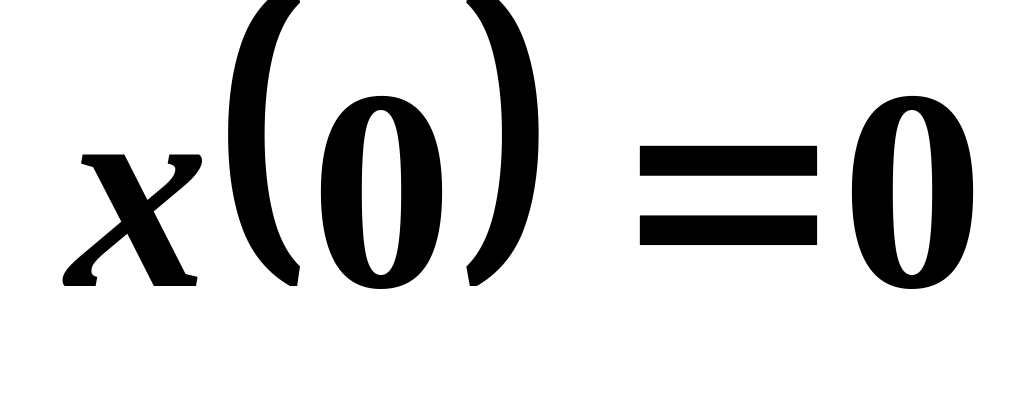и проекция скорости .

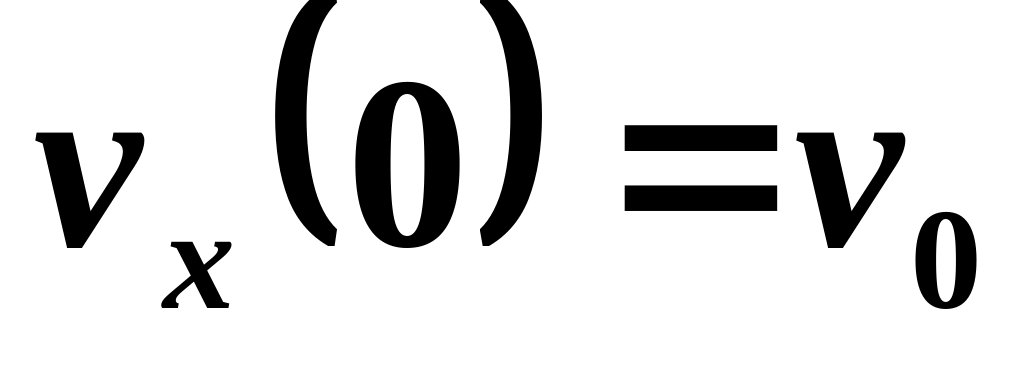5. Тело массой совершает затухающие колебания с максимальной амплитудой , начальной фазой 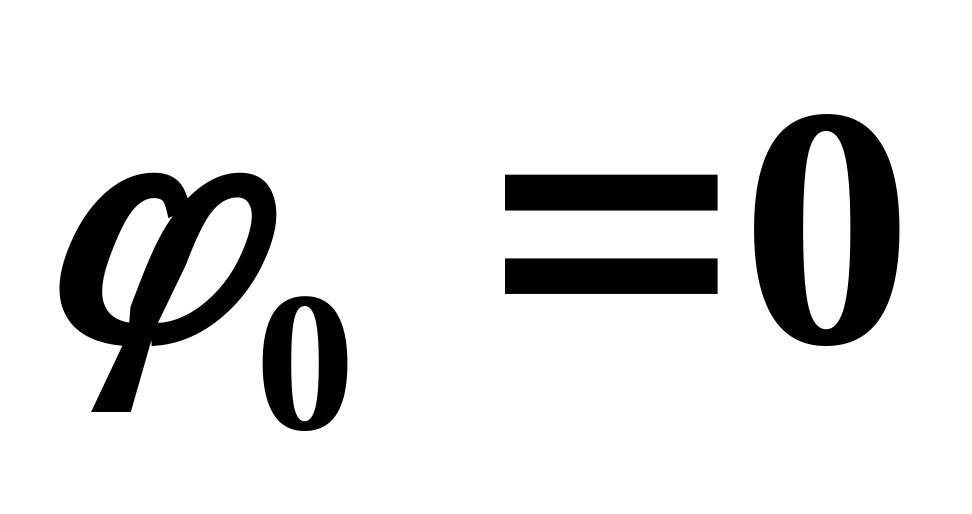и коэффициентом затухания . Под действием внешней периодической силы устанавливаются вынужденные колебания, уравнение которых имеет вид . Найти уравнение собственных колебаний и внешнюю силу.

Занятие № 9 Кинематика твердого тела

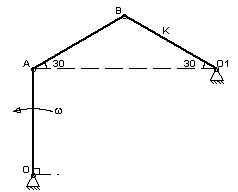1. О пределить скорость точки 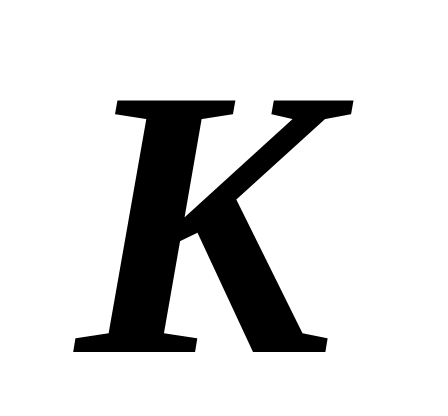в момент, соответствующий 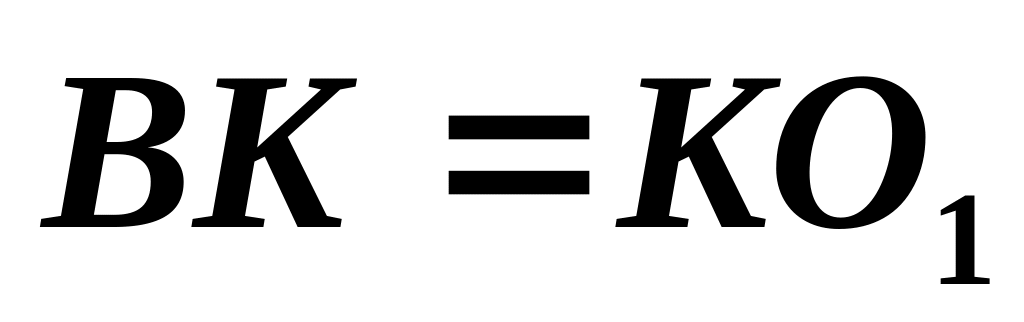, , 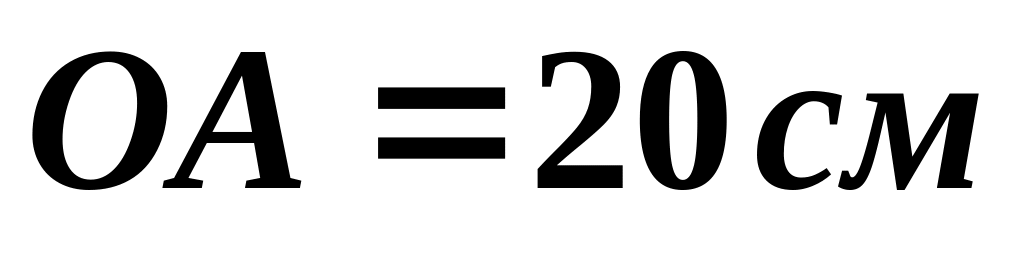стержень 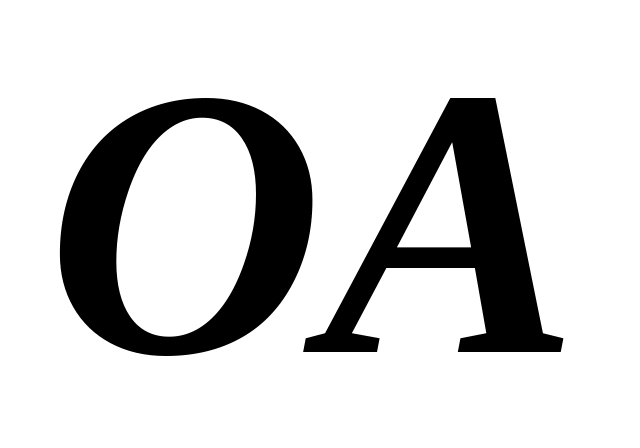вращается с угловой скоростью 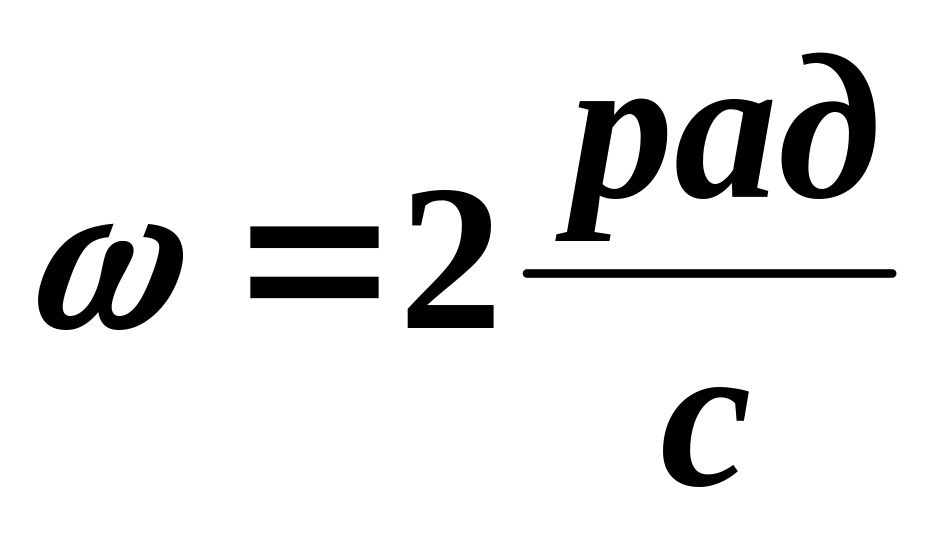относительно оси , перпендикулярной плоскости рисунка, в которой происходит движение всех стержней.

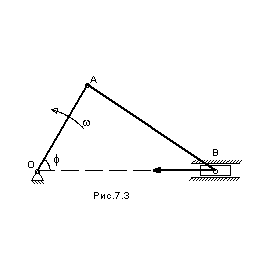
2. В кривошипно-ползунном механизме кривошип длиной вращается с угловой скоростью . Длина шатуна 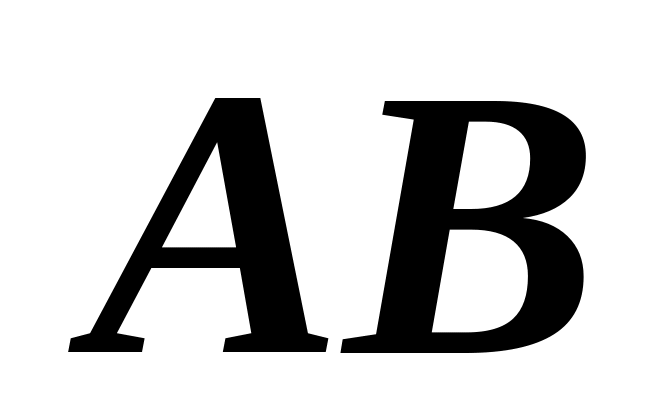равна . При заданном угле определить: 1) скорость ползуна ; 2) положение точки шатуна , имеющей наименьшую скорость; 3) угловую скорость шатуна.

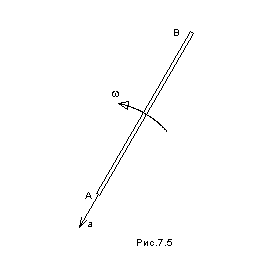
3. Стержень длиной 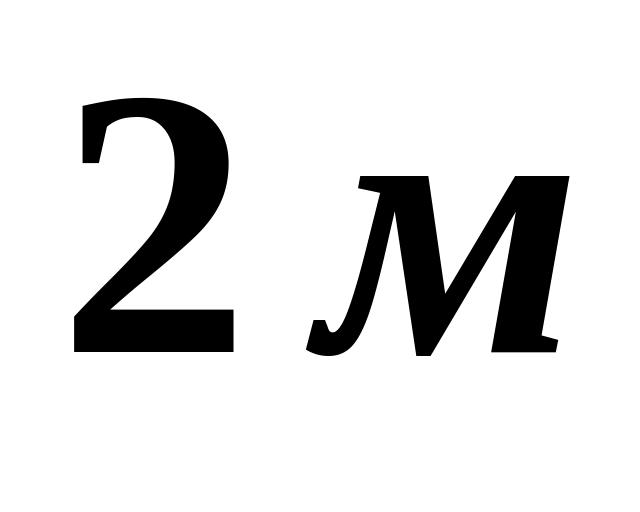совершает плоское движение. Найти ускорение точки , если ускорение точки равно 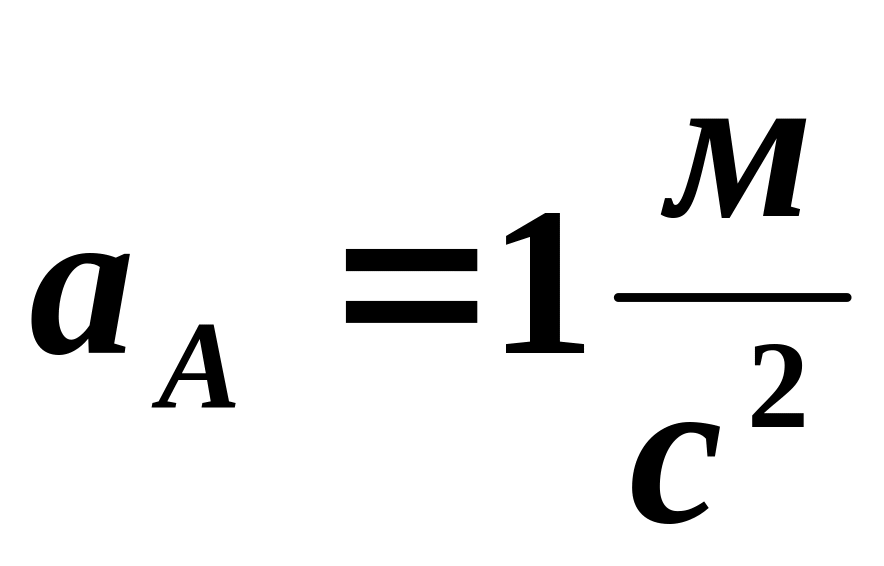, угловая скорость стержня 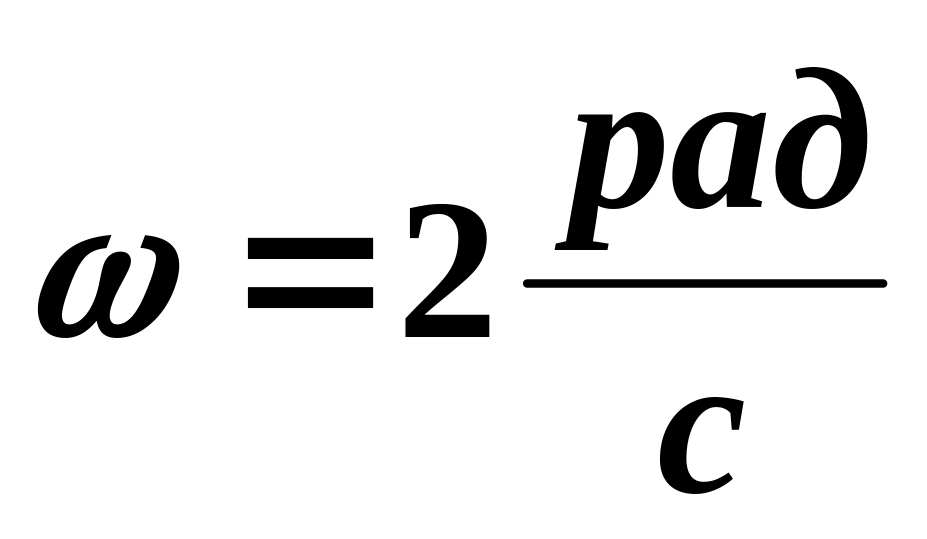, угловое ускорение .

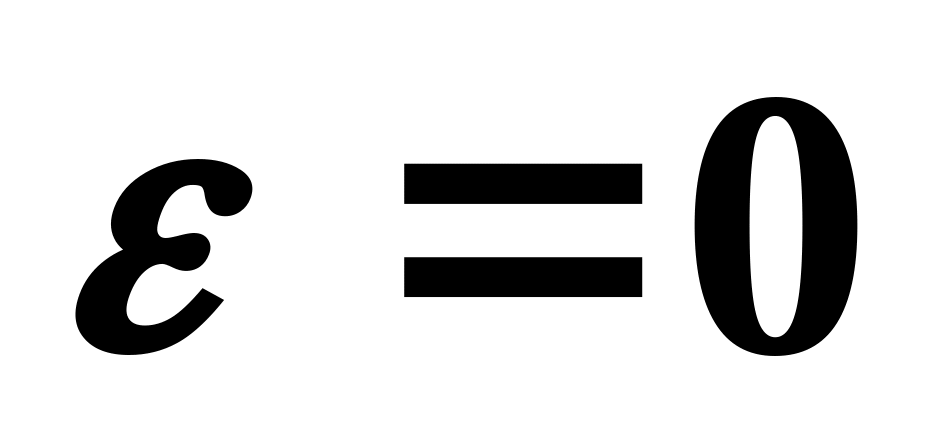4. К 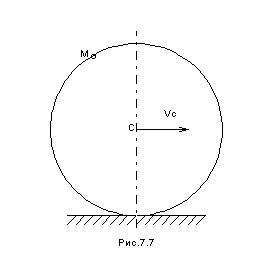олесо катится по прямолинейному рельсу так, что скорость 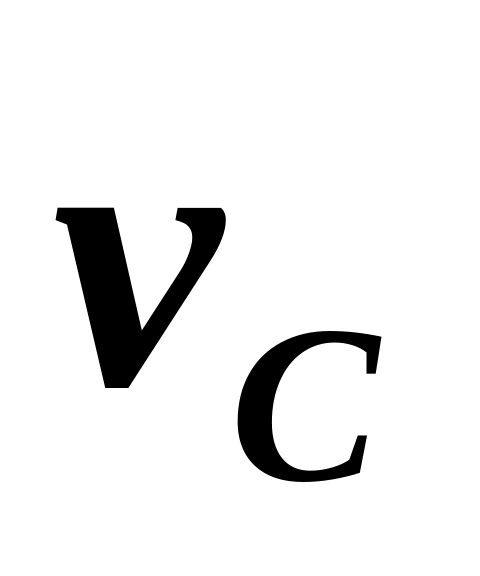его центра постоянна. Определить ускорение точки обода колеса.

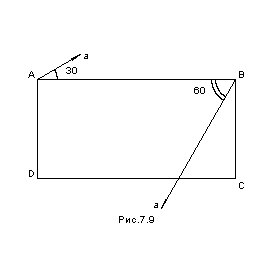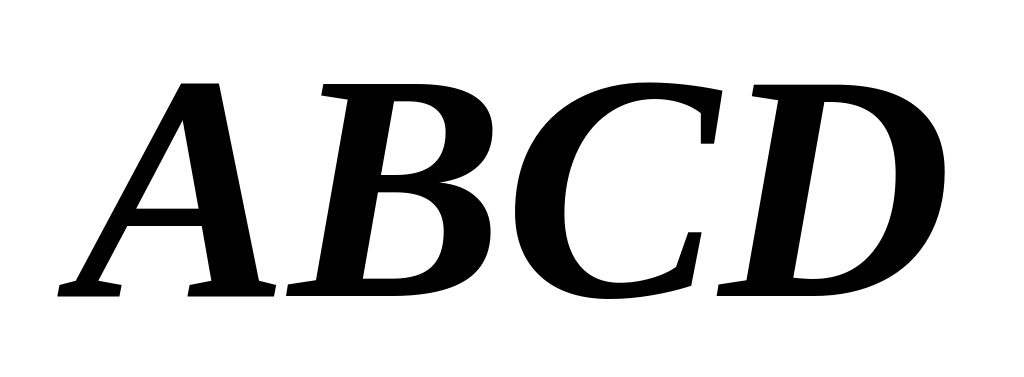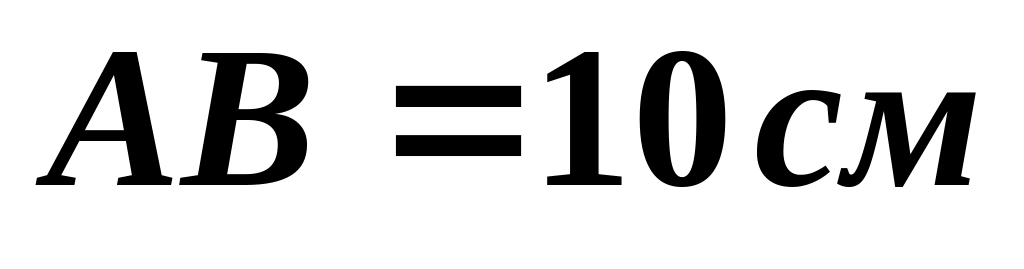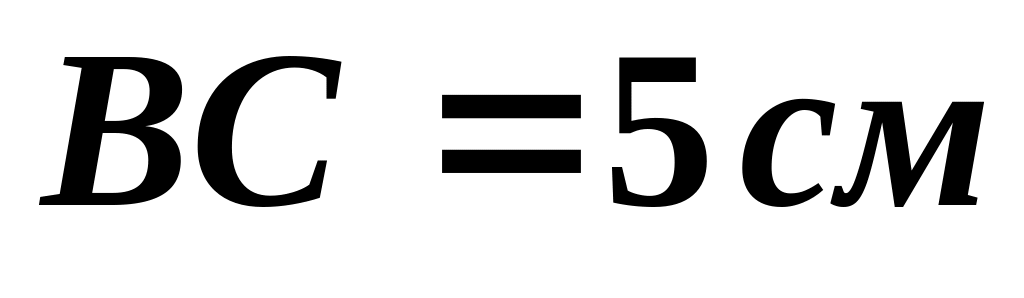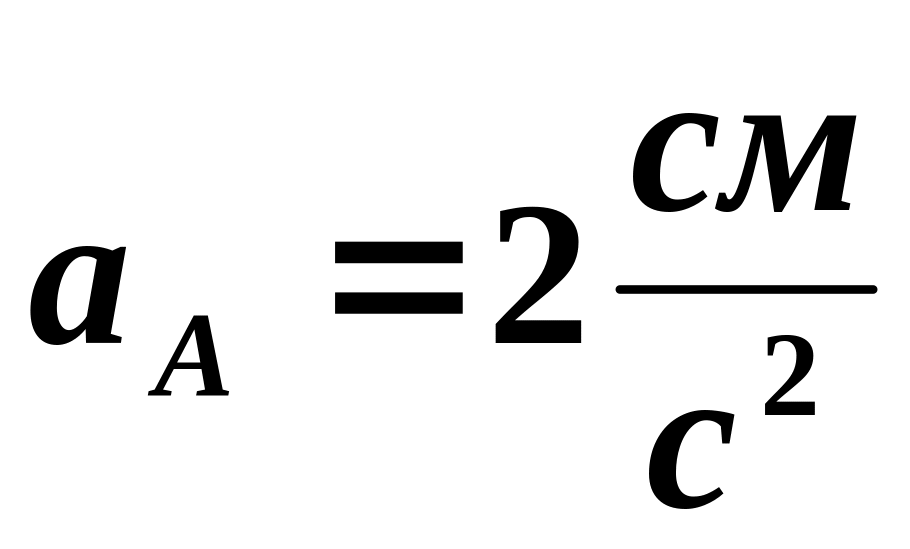
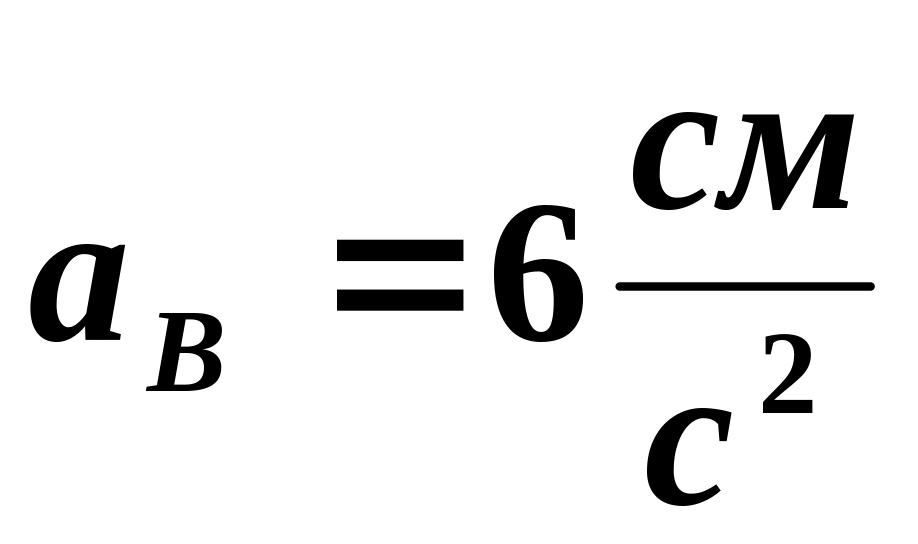5. П рямоугольник со сторонами , совершает плоское движение. В данный момент ускорения . Определить ускорение точки , а также мгновенные угловые скорость и ускорение прямоугольника.