Занятие № 4 Уравнения Лагранжа.

1. К оси 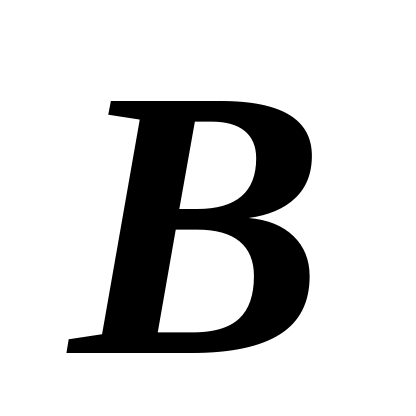однородного цилиндра массой , который может кататься без скольжения по горизонтальной плоскости, прикреплен шарнирно однородный стержень 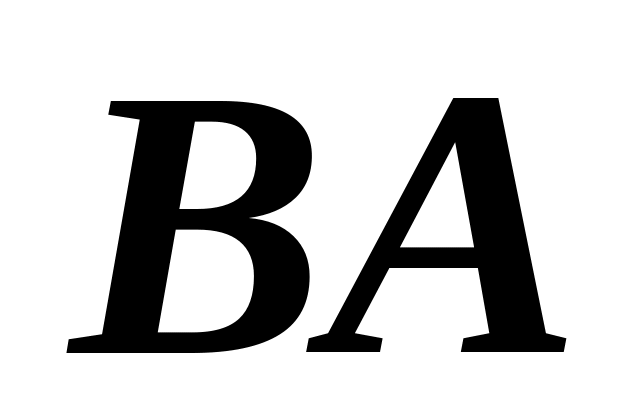длиной и массой . Составить функцию Лагранжа и дифференциальные уравнения движения системы.

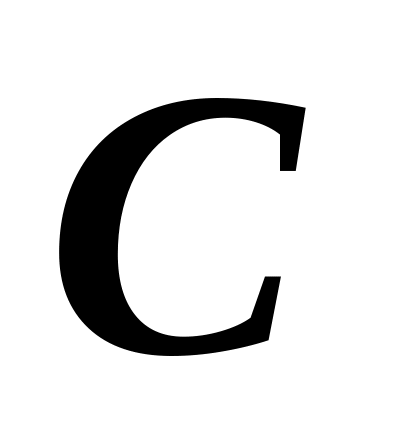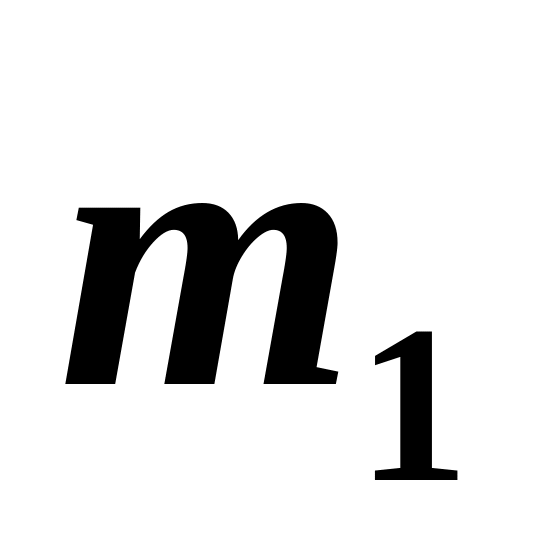2. С помощью уравнений Лагранжа найдите ускорение груза массой . Тела и считать однородными цилиндрами равного радиуса и массами и соответственно. Нить невесомая и нерастяжимая; сопротивлением движению пренебречь.

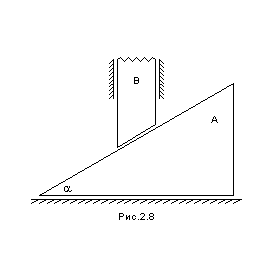
3. С помощью уравнений Лагранжа найдите ускорение тела . Массы тел и равны и соответственно. Трением пренебречь.

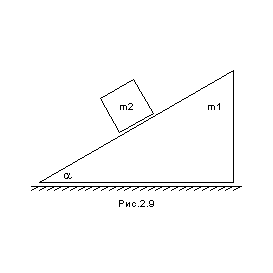
4. С помощью уравнений Лагранжа найдите ускорение тел. Трением пренебречь.

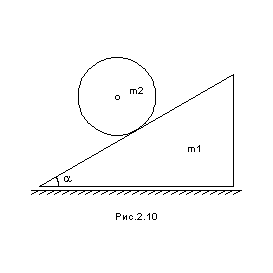
5. Клин массой . находится на гладкой горизонтальной поверхности. С клина скатывается без скольжения однородный цилиндр массой . Используя уравнения Лагранжа, найдите ускорение клина.

Занятие № 5 Уравнения Лагранжа и законы сохранения

1. На одном конце легкой нерастяжимой нити, перекинутой через легкий неподвижный блок, укреплен груз массой . По другому концу нити перемещается обезьяна массой по закону 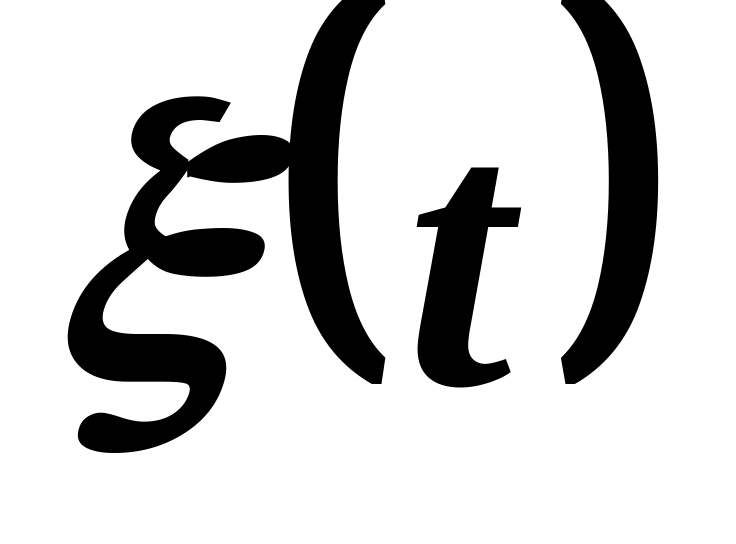относительно нити. Найти функцию Лагранжа системы и закон движения обезьяны относительно Земли. Сопротивлением движению пренебречь.

2. Частица массой движется по гладкой кривой 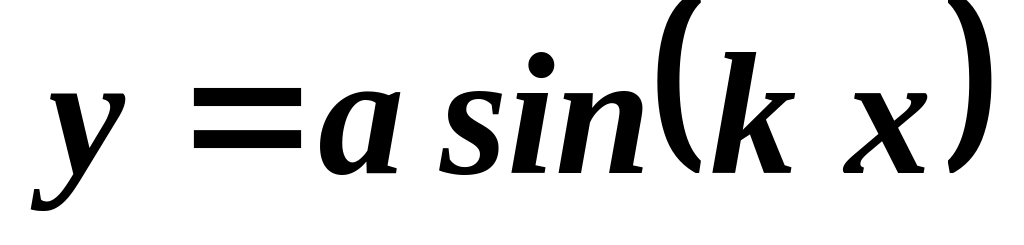. Ось 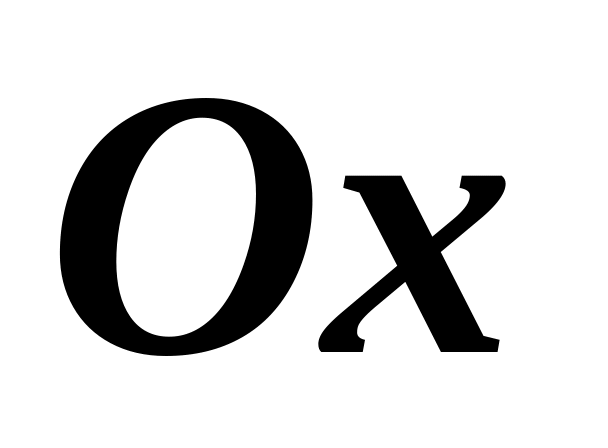горизонтальна, ось образует угол с вертикалью. Найти функцию Лагранжа и интеграл энергии частицы.

3. Частица массой движется в однородном поле тяжести по циклоиде: 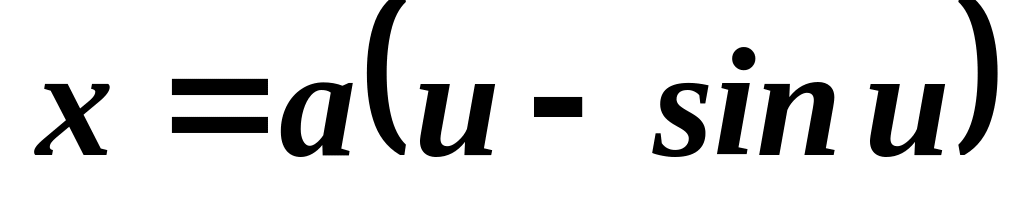, 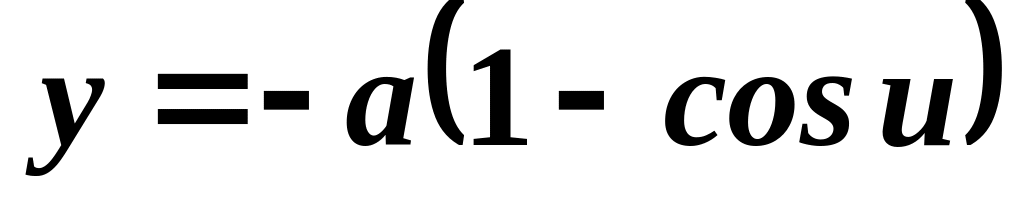. Ось направлена вертикально вверх. Найти функцию Лагранжа, первый интеграл и закон движения.

4. Два шарика с массами и , соединенные легкой пружиной с жесткостью и длиной в ненапряженном состоянии, движутся по гладкой горизонтальной прямой. Найти лагранжиан и интегралы движения.

5. Частица массой движется по гладкой поверхности конуса с углом 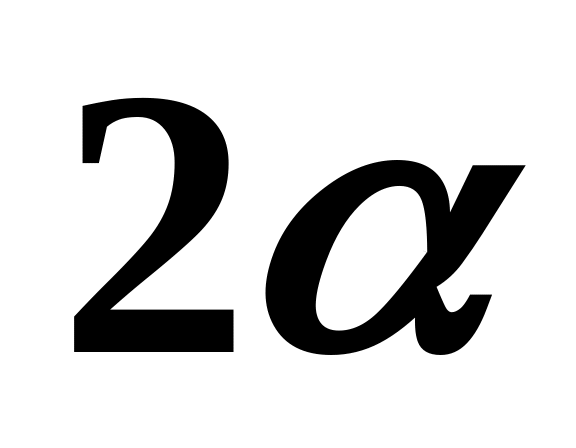при вершине. Ось конуса вертикальна. Найти функцию Лагранжа, первые интегралы и закон движения частицы.

Занятие № 6 Движение в центральном поле

1. Найти время свободного падения тела на Солнце с расстояния, равного радиусу орбиты Земли.

2. В поле тяготения Солнца движется комета с периодом обращения 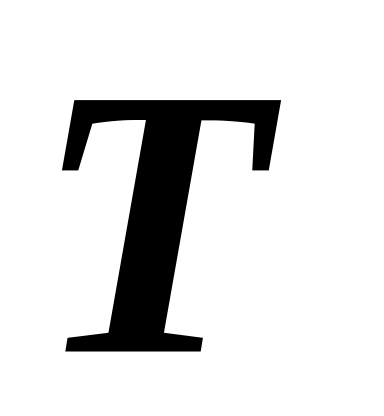. В перигелии расстояние от Солнца до кометы равно 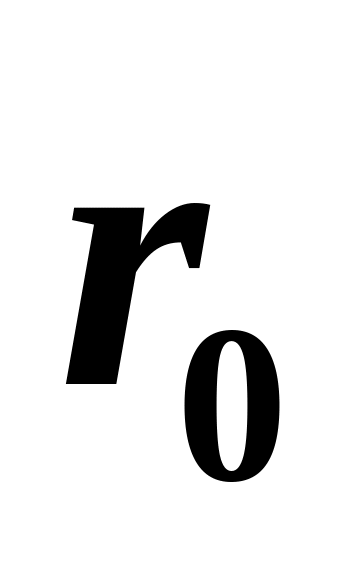. Найти расстояние от Солнца до афелия орбиты кометы, зная период обращения Земли вокруг Солнца и значение большой полуоси орбиты Земли.

3. Спутник Луны двигался по круговой орбите с радиусом и после кратковременного торможения перешел на эллиптическую орбиту, касательную к лунной поверхности. Найти время его падения на Луну.

4. Найти зависимость полной механической энергии планеты массой от большой полуоси ее эллиптической орбиты вокруг Солнца.

5. Известны параметр 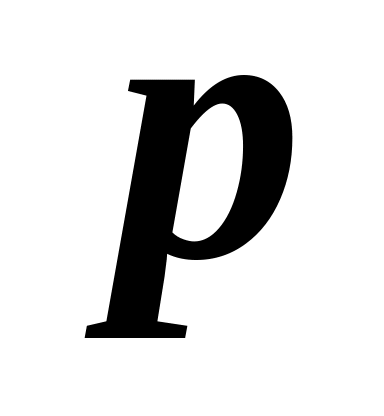и эксцентриситет 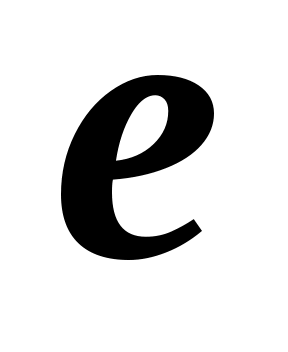орбиты частицы, движущейся в центральном поле притяжения кулоновского типа. Найти скорость частицы как функцию расстояния от центра поля.