Занятие 1 Кинематика материальной точки.

1. Радиус-вектор частицы 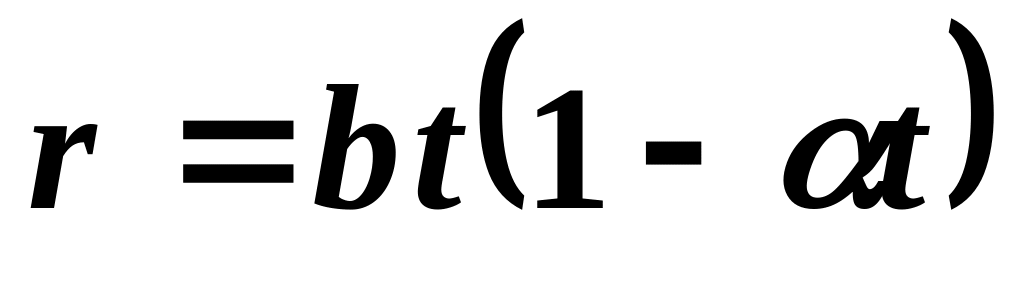, где 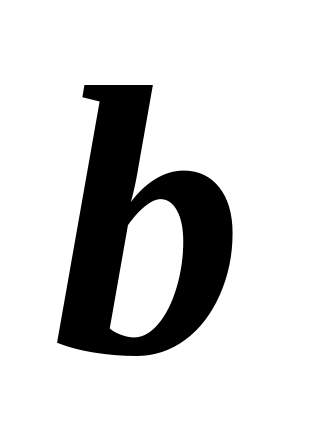– постоянный вектор, – положительная постоянная. Найти: а) скорость и ускорение частицы в зависимости от времени 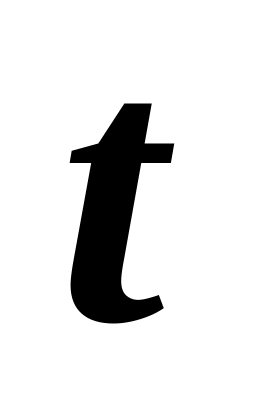; б) промежуток времени, по истечении которого частица вернется в исходную точку, и ее путь при этом.

2. Частица движется по прямой со скоростью 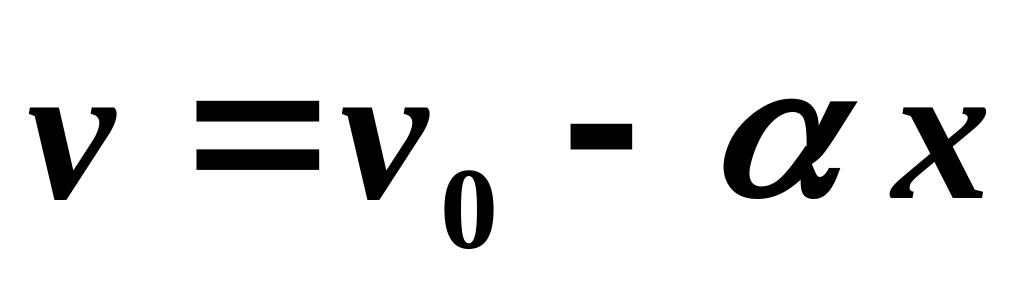, где и – положительные постоянные. В момент времени 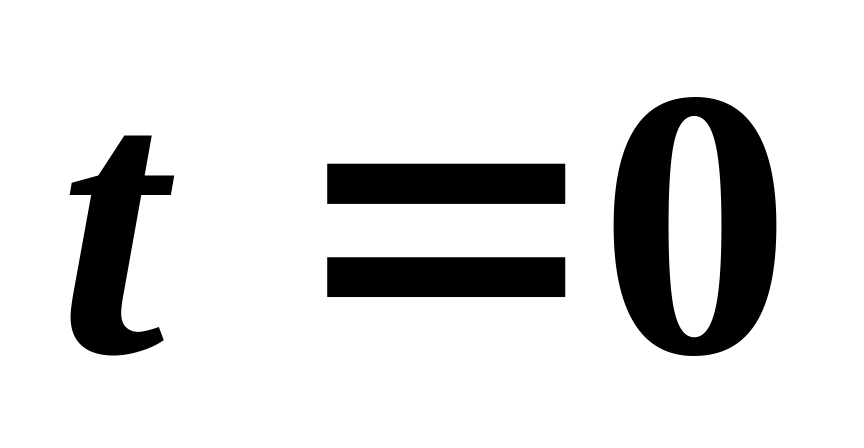координата 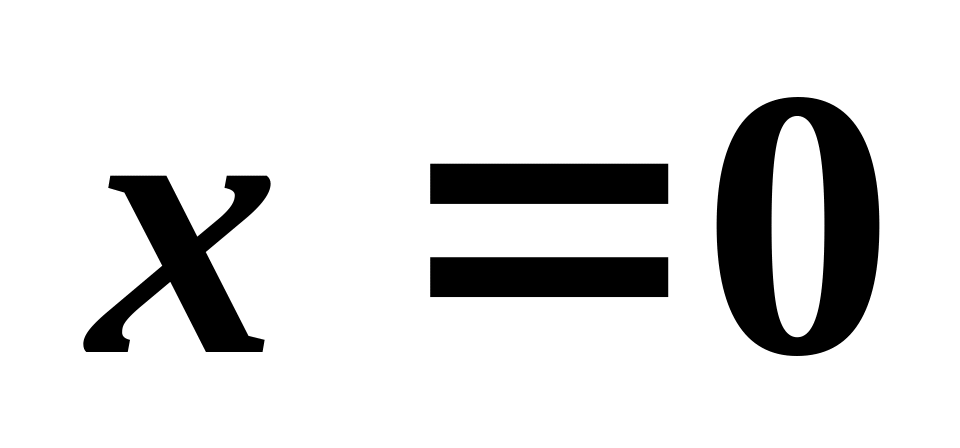. Найти зависимости скорости, ускорения и координаты от времени.

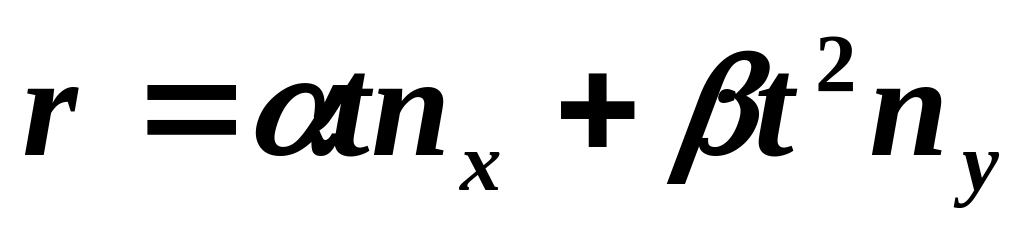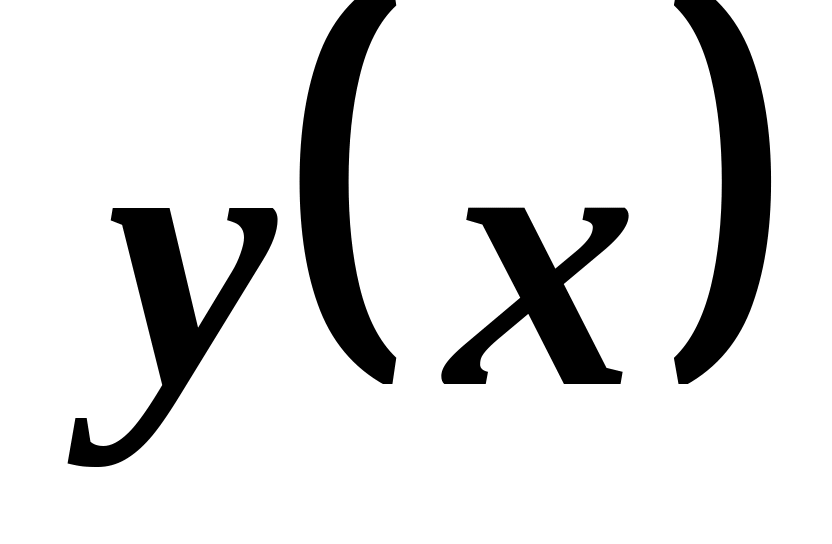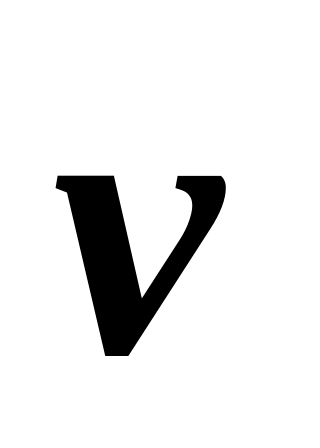3. Радиус-вектор частицы , где и – положительные постоянные. Найти а) уравнение траектории ; б) зависимости от времени скорости , ускорения и модулей этих величин; в) зависимость от времени угла между векторами и .

4. Ускорение частицы постоянно и направлено против положительного направления оси 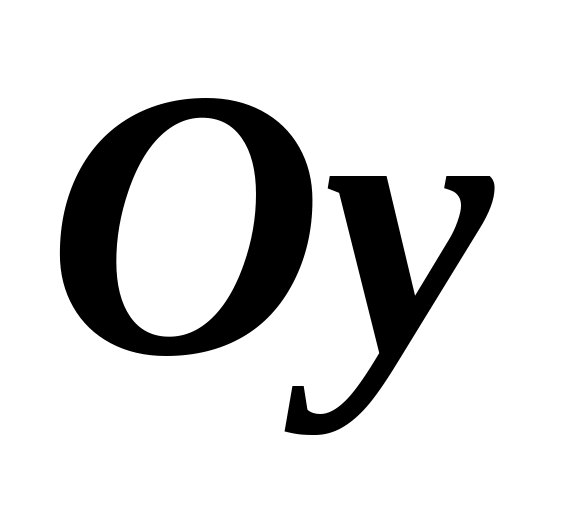. Уравнение траектории 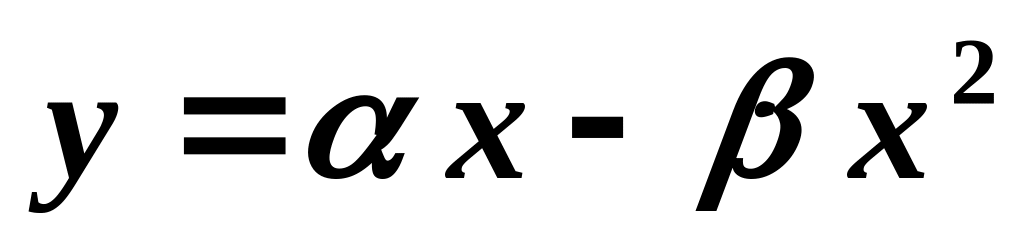, где и – положительные постоянные. Найти скорость в начале координат.

5. Частица движется по эллипсу с ускорением, параллельным оси . Найти ускорение как функцию координаты , если , .

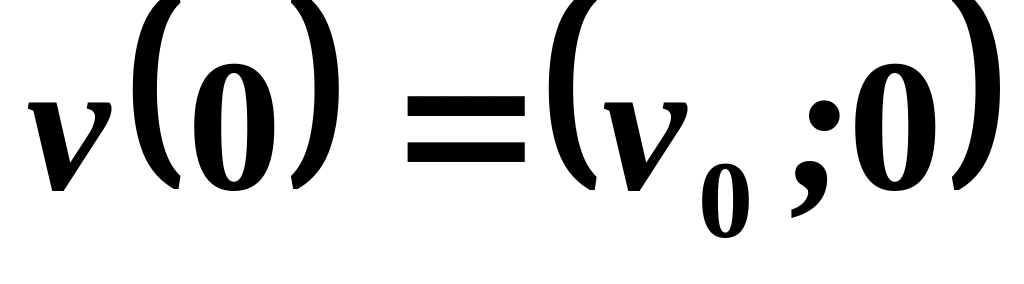Занятие 2 Уравнения движения материальной точки.

1. Частица движется в плоскости 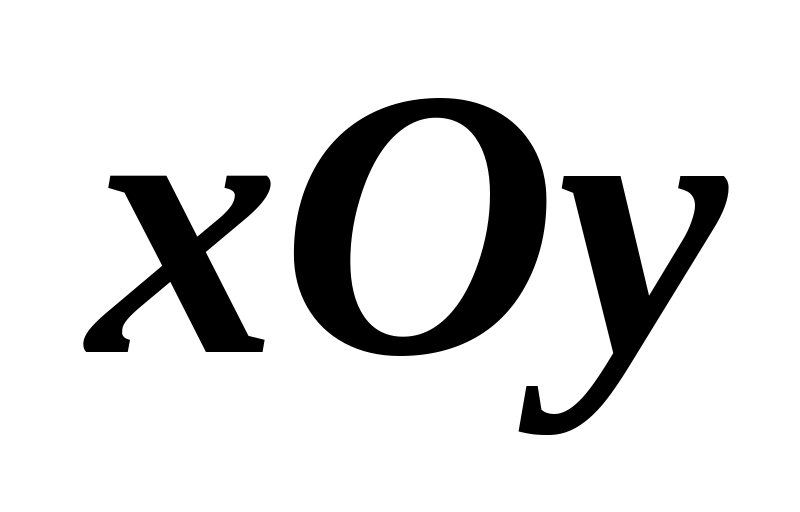со скоростью , где и – положительные постоянные. В начальный момент 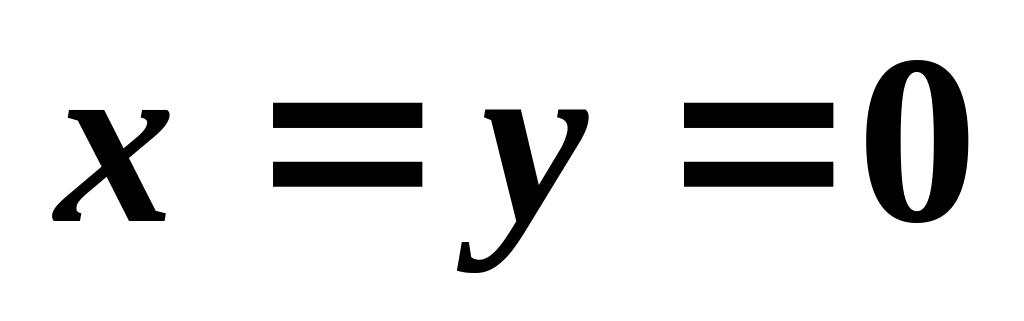. Найти уравнение траектории и радиус ее кривизны в зависимости от координаты .

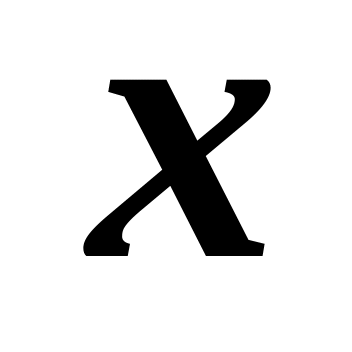2. На наклонную под углом к горизонту плоскость с высоты 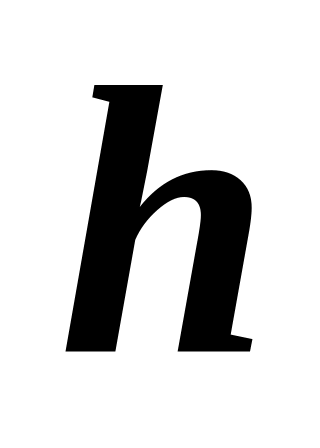начал падать мяч. На каком расстоянии от места падения он упадет на плоскость вторично, если соударение упругое.

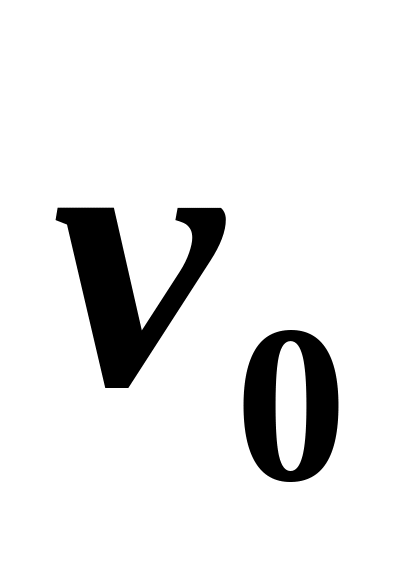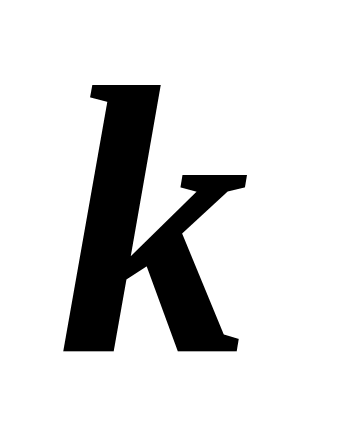
3. Мяч, брошенный с земли со скоростью под углом к горизонту, прыгает по горизонтальной поверхности. Отношение скоростей мяча до и после удара постоянно и равно . Найти время движения мяча и расстояние, пройденное им по горизонтали.

4. Выразите ускорение частицы в сферических координатах.

5. Выразите ускорение частицы в цилиндрических координатах.

Занятие № 3 Функция Лагранжа.

1. Составить функцию Лагранжа для математического маятника массой 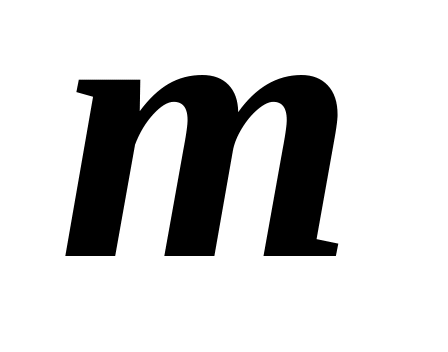и длиной с неподвижной точкой подвеса.

2. Составить функцию Лагранжа для математического маятника массой и длиной , точка подвеса которого движется горизонтально с постоянной скоростью 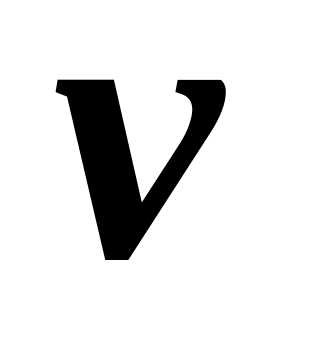в плоскости качаний маятника.

3. Составить функцию Лагранжа для математического маятника массой и длиной , точка подвеса которого движется по наклоненной под углом к горизонту прямой с постоянным ускорением в плоскости качаний маятника.

4. Составить функцию Лагранжа для математического маятника массой и длиной , точка подвеса которого совершает вертикальные колебания по закону 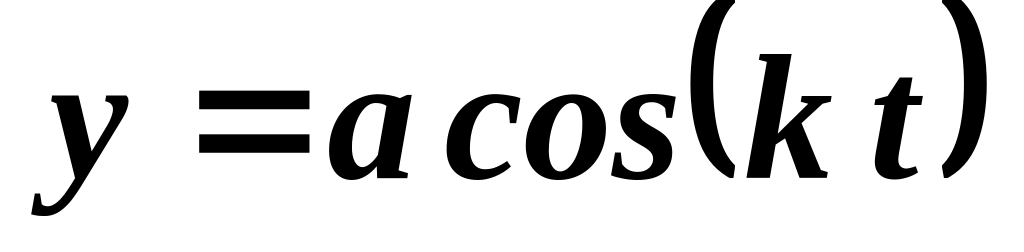, где и – положительные постоянные.

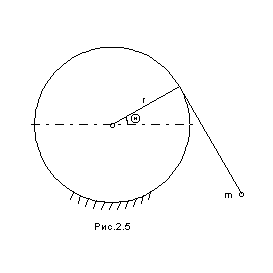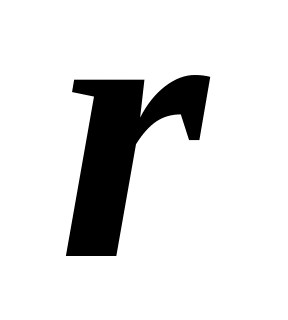5. С оставить функцию Лагранжа и найти уравнение движения маятника, представляющего собой материальную точку массой , подвешенную на невесомой нерастяжимой нити, навернутой на неподвижный горизонтальный цилиндр радиусом . Длина свисающей в равновесии части нити равна .