14

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»

Институт радиоэлектроники и информационных технологий - РТФ

Кафедра Автоматика и информационные технологии

Численные методы решения систем нелинейных уравнений

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К лабороторной работе ПО ДИСЦИПЛИНЕ «Численные методы»

2011

Составитель И.А.Селиванова, ст.преподаватель.

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ: Методические указания к лабораторной работе по дисциплине «Численные методы»

Указания предназначены для студентов всех форм обучения направления 230100 – «Информатика и вычислительная техника».

Ó ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н.Ельцина», 2011

Содержание

3

1. Постановка задачи 4

2. Метод Ньютона, его реализации и модификации 4

2.1. Метод Ньютона 4

2.2. Модифицированный метод Ньютона 8

2.3. Рекурсивный метод Ньютона. 8

3. Метод простых итераций 10

4. ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ 12

5. Варианты заданий. 13

Список литературы 14

1. Численные методы решения систем нелинейных уравнений

1. Постановка задачи

Дана система нелинейных уравнений с неизвестными:

(1.1)

где , - нелинейные функции, определенные и непрерывные в некоторой области . Систему (1.1) можно представить в векторном виде:

(1.2)

где , .

Требуется найти такой вектор , который при подстановке в систему (1.1) превращает каждое уравнение в верное числовое равенство.

Для всех рассматриваемых далее методов требуется находить начальное приближение . В случае это можно сделать графически, определив координаты точки пересечения кривых, описываемых уравнениями или .

2. Метод Ньютона, его реализации и модификации

2.1. Метод Ньютона

Для решения системы (1.1) воспользуемся методом последовательных приближений. Предположим, что найдено -ое приближение одного из изолированных корней векторного уравнения (1.2). Тогда точный корень уравнения можно представить в виде:

(2.1.1)

где - поправка (погрешность) корня на -ом шаге.

Подставив выражение (2.1.1) в (1.2), получим:

(2.1.2)

Предположим, что функция - непрерывно дифференцируема в некоторой выпуклой области, содержащей и . Тогда левую часть уравнения (2.1.2) разложим в ряд Тейлора по степеням малого вектора , ограничиваясь линейными членами:

(2.1.3)

Под производной следует понимать матрицу Якоби системы функций , относительно переменных , то есть:

(2.1.4)

Формула (2.1.3) может быть записана в следующем виде:

(2.1.5)

Отсюда, предполагая, что матрица - неособенная, получим:

(2.1.6)

Теперь, подставив выражение (2.1.6) в формулу (2.1.1), окончательно получим:

(2.1.7)

Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения можно взять приближенное (грубое) значение искомого корня.

Для останова процесса вычислений в быстросходящихся методах таких, как метод Ньютона, методы секущих и т.п., часто вполне успешно применяют простой критерий:

,

(2.1.8)

Это можно объяснить двумя причинами. Во-первых, оценки погрешности здесь довольно «дороги». Имеется в виду как их получение (особенно для различных модификаций базовых методов), так и их реальное применение. Во-вторых, в силу своей быстрой сходимости, к моменту достижения требуемой малости нормы поправки эти методы набирают такую скорость, что зачастую «проскакивают» установленный порог точности. Т.е. выход по критерию (2.1.8) дает значение значительно (иногда на несколько порядков) меньшее, чем . Отслеживать факт сходимости в процессе итерации для того, чтобы реагировать на возможную расходимость в случаях, когда заранее не обеспечены условия сходимости применяемого метода, можно с помощью текущих проверок на уменьшение от шага к шагу поправок и невязок, т.е. выполнение неравенств:

и

(2.1.11)

Методика решения задачи

1. Задать начальное приближение и малое положительное число (точность). Положить .

2. Найти значение выражения .

3. Вычислить следующее приближение: .

4. Если и 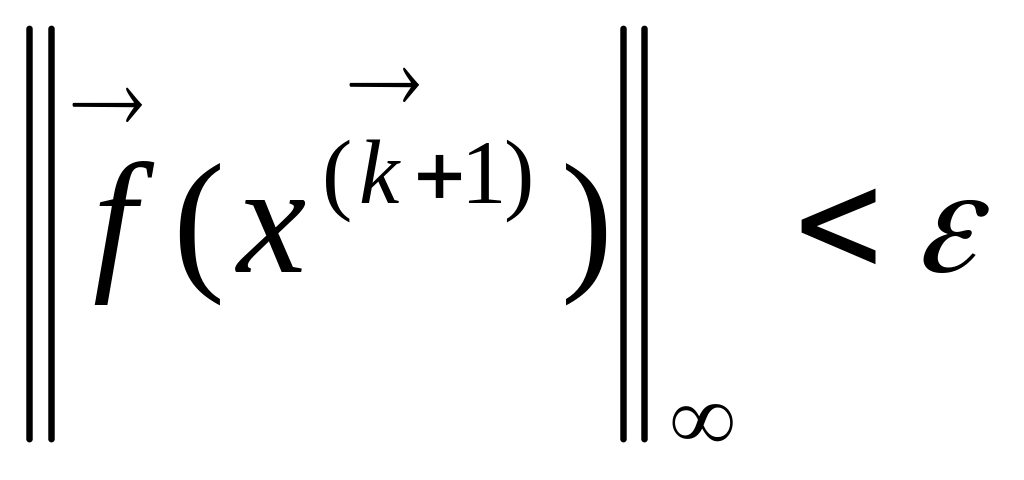, процесс закончить и положить . Иначе, положить и перейти к п.2.

Пример 1. Решить систему методом Ньютона с точностью .

1. Для выбора начального приближения найдем координаты точек пересечения кривых, соответствующих первому и второму уравнениям (рис. 1).

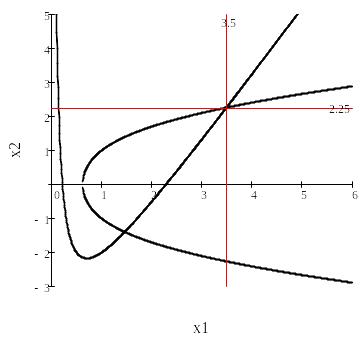
Рис. 1 Выбор начального приближения

Выберем начальное приближение . В поставленной задаче . Положим .

2⁰. Так как

то

,

,

.

3⁰. Вычислим

4⁰. Так как , то положим и перейдем к п.2.

2¹. Так как

3¹. Вычислим

4¹. Так как , то положим и остановим вычисления. Результаты расчетов приведены в табл. 1.

Таблица 1

k	0	1	2
x1(k)	3,500000	3,488164032	3,487443000
x2(k)	2,200000	2,262718691	2,261628964
	-	0,062718692	0,001089727
	0,299999	0,003941099	0,000001215

Точность достигнута за две итерации.

К недостаткам метода Ньютона следует отнести:

• необходимость задавать достаточно хорошее начальное приближение;

• отсутствие глобальной сходимости для многих задач;

• необходимость вычисления матрицы Якоби на каждой итерации;

Достоинством метода является квадратичная сходимость из хорошего начального приближения при условии невырожденности матрицы Якоби [1].