5.4. Метод Ритца-Тимошенко.

Пример 1. Проиллюстрируем применение метода Ритца-Тимошенко на примере той же шарнирно опертой по всему контуру прямоугольной пластины.

Следуя процедуре этого метода, зададим искомую функцию приближенно в виде частичной суммы ряда

(5.24)

где — искомые числовые параметры, а аппроксимирующие функции , выбранные в форме

(5.25)

обеспечивают выполнение геометрических граничных условий

(5.26)

Система функций ( ) — линейно независимая, полная и ортогональная в области . В силу (5.26) для полной энергии изгиба пластины справедливо упрощенное выражение (4.6):

(5.27)

Дальнейшая схема реализации метода Ритца-Тимошенко

требует подстановки (5.24) в (5.27), интегрирования по области , после чего она завершается требованием выполнения необходимого условия экстремума (минимума) функции :

(5.28)

Отсюда и находятся искомые величины . Заметим, однако, что

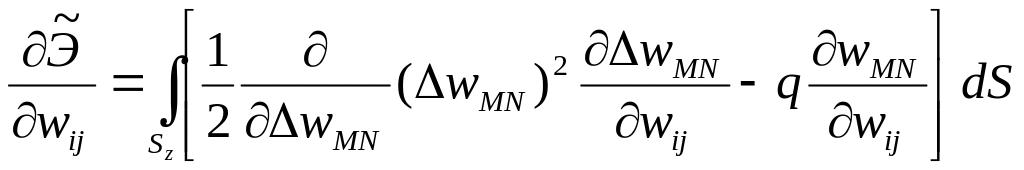
Это позволяет избежать стандартное возведение в квадрат ряда типа (5.24) и, тем самым, сократить объем выкладок. Имея в виду, что

с учетом условий ортогональности (см. (5.7), (5.25))

(5.29)

из уравнений (5.28) находим

Здесь

(5.30)

Итак, искомое приближенное решение имеет вид

(5.31)

и, как и следовало ожидать, в пределе при переходит в точное решение (5.9).

Пример 2. Проиллюстрируем метод на примере пластины, свободной от нагрузки по всему контуру поперечного сечения.

Функционал полной энергии такой пластины представим в форме (4.5)

, (4.5)

где искомая функция прогиба ищется в виде ряда

(5.32)

Здесь система функций выбрана так, чтобы смещения были возможными, то есть линейно независимыми, непрерывными, полными и удовлетворяющими на контуре пластины всем геометрическим граничным условиям. При этом функции могут удовлетворять и статическим граничным условиям, но это не обязательно.

Если это возможно, то функция двух переменных задается в виде комбинации функций одной переменной, так

При выбранных функциях , подставив (5.32) в (4.5) и произведя интегрирование, мы получим функцию, зависящую только от констант . Условие ее минимума

(5.33)

Система (5.33) всегда относительно констант линейна

,

где при всех четырех опертых кромках

Здесь

где символом (k) обозначены функция, ее первая и вторая производные k=0,1,2.

5.5. Метод Бубнова-Галеркина.

При иллюстрации и этого метода мы вновь ограничимся рассмотренным выше случаем шарнирно опертой по всему контуру прямоугольной пластины, т.е. вернемся к Примеру 1. По-прежнему зададим искомую функцию приближенно в виде (5.24), (5.25), обеспечивающем выполнение всех краевых условий задачи (5.2), (5.3).

Для нахождения искомых числовых параметров в методе Бубнова-Галеркина служит система

Подставляя сюда выражение (5.24), приходим к равенству

из которого с учетом условия ортогональности (5.29) и формулы (5.31) находим

Как и следовало ожидать, мы получили тот же результат, что и в методе Ритца-Тимошенко (см. (5.31)).

Перейдем к Примеру 2.

Решение задачи, как и в предыдущем случае, ищется в форме ряда (5.32) с теми же требованиями к аппроксимирующим функциям. Различие состоит в следующем.

По методу Ритца функционал полной энергии минимизируется впрямую, то есть ищется такая комбинация констант, которая обеспечивает этому функционалу минимум на ограниченном множестве функций .

По методу Бубнова-Галеркина условие минимума этого функционала записывается по правилам вариационного исчисления

(5.33)

где под контурными интегралами стоит разность между внутренними силовыми факторами на контуре пластины

            

и соответствующими им внешними факторами, , если таковые приложены по контуру пластины.

Точное решение задачи дает экстремаль, удовлетворяющая уравнению Эйлера и естественным граничным условиям на контуре пластины

Если выбором функций выполнены не только кинематические, но ВСЕ граничные условия задачи, то граничные члены в (5.33) обнуляются, и мы имеем только условие

В силу произвольности и независимости вариаций при константах равенство нулю возможно только при обнулении констант при каждом члене ряда.

(5.34)

Выражение (5.34), расписанное с помощью (5.32)

(5.35)

где

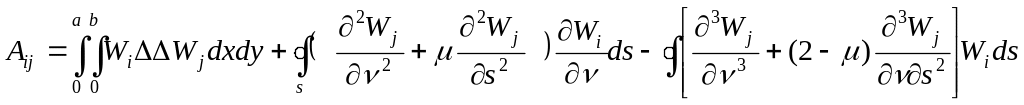
(i=1,2,…,n j=1,2,…,n) (5.36)

Отметим два факта.

При выборе одних и тех же функций коэффициенты системы (5.35), несмотря на разницу в форме представления, по существу всегда одинаковы.

Если функции выбраны так, что статические граничные условия выполнены, то контурные интегралы в (5.36) исчезают.

(i=1,2,…,n j=1,2,…,n)