3. Граничные условия

Для завершения постановки задач теории пластин необходимо сформулировать еще краевые условия на поперечной граничной поверхности в терминах обобщенных сил и смещений.

Остановимся сначала на постановке геометрических граничных условий. Для прямоугольной пластины, на всех кромках которой имеют место именно такие условия, они записываются в общем случае таким образом

где справа стоят известные обобщенные смещения, предписываемые на соответствующих кромках наложенными на них связями. В частности, если все правые части тождественно равны нулю, то мы приходим к условиям жесткого закрепления (защемления) прямоугольной пластине по всем кромкам

которые условимся помечать штриховкой (см. рис. 3.1 а). На защемленной кромке запрещаются прогиб и поворот поперечного сечения пластины, содержащего эту кромку, относительно ее самой.

К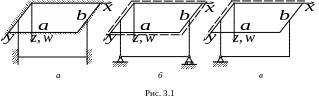 смешанным граничным условиям относятся условия на шарнирно или свободно опертых кромках (условимся помечать их штриховой линией, параллельной рассматриваемой кромке). Свободно опертые кромки (например, кромка на рис. 3,1 б) в отличие от шарнирно опертых (например, кромка на рис. 3,1 б) допускают смещения срединной поверхности в ее плоскости, что существенно при рассмотрении плоского напряженного состояния пластины. Поэтому в теории изгиба пластин эти кромки неразличимы. По определению шарнирно опертая кромка не допускает прогиба и не передает изгибающий момент. Пусть, например, таковой является кромка . Тогда на ней

В силу первого равенства . Поэтому условия шарнирного опирания рассматриваемой кромки принимают окончательно вид

Аналогично показывается, что в случае шарнирно опертой кромки должны выполняться условия

Подобные же условия на других кромках записываются очевидным образом.

Статические граничные условия реализуются на свободных кромках. Незагруженными такими кромками являются кромки и на рис. 3.1 в. На них должны обращаться в нуль обобщенные силы пластины, т. е.

Подставляя сюда соответствующие выражения (2.2), (2.12), приходим к равенствам

В случае загруженных кромок имеем соответственно

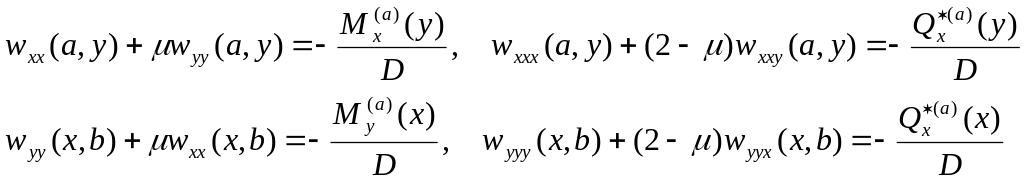
где , , , — заданные на соответствующих кромках положительно действующие моментные и силовые погонные нагрузки.

4. Полная энергия изгиба пластины

Получим выражение полной энергии изгиба пластины, предполагая для простоты, что внешние силы на пластину представлены только поверхностной нагрузкой .

По определению полная энергия изгиба пластины равна разности потенциальной энергии и работы внешних сил :

(4.1)

В свою очередь потенциальная энергия выражается через свою плотность известным соотношением

(4.2)

где интегрирование осуществляется по всему объему, занятому пластиной. В рамках гипотезы Кирхгоффа формула Клапейрона имеет вид

или, если учесть (1.7), то

Подставим это выражение в (4.2) и выделим интегрирование по толщине пластины. Тогда получим

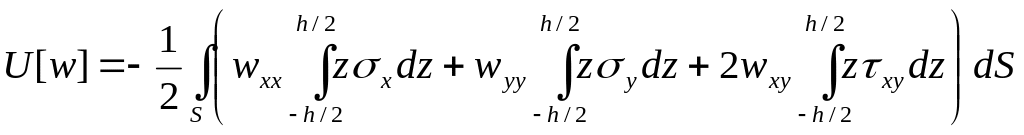
Вспоминая (2.2), находим формулу

которая после замены погонных моментов их выражениями через прогиб приводит к равенству

(4.3)

Работа внешних сил, очевидна, равна

(4.4)

Искомое выражение для полной энергии изгиба пластины вытекает из формул (4.1), (4.3), (4.4) и имеет вид

(4.5)

Можно показать, что если краевые условия таковы, что на всех кромках прямоугольной пластины , то

(4.6)