4.2 Наблюдение дифракционной картины от щели

4.2.1. Регулировкой высоты установить тест-объект так, чтобы лазерный луч попадал на окружность С. По заданию преподавателя, вращением Т-О установить необходимую щель так, чтобы лазерный луч попадал по центру этой щели.

4.2.2. Прикрепить белый лист бумаги к экрану. Плавно изменяя положение Т-О, добиться четкого и наиболее яркого изображения дифракционной картины (чередование красных полос см. рис.7).

4.2.3. Карандашом перенести на прикреплённый лист наблюдаемую дифракционную картину.

4.2.4. Вращением Т-О установить последовательно 2-ю и 3-ю щели и зарисовать наблюдаемые дифракционные картины.

4.2.5. По полученным рисункам измерить:

а_n^min – расстояние между двумя симметричными минимумами n-го порядка;

a_n^max – расстояние между двумя симметричными максимумами n-го порядка; n = 1, 2.

4.2.6.Результаты измерения занесите в таблицу 1.

Таблица 1

№ щели	a1min	a2min	a1max	a2max	φ1min =	φ2min =	φ1max =	φ2max =
1
2
3
4

где L – расстояние от тест-объекта Т-О до экрана. L =..............................,м

4.2.7. По данным таблицы 1 вычислить значения ширины щели b, используя условия минимума и максимума дифракции:

Условие минимума:

b sin φ_m^min = ± m λ, m=1,2.

Условие максимума:

b sin φ_m^max = ±(2m+1)/2 , m=1,2,

где φ_m – угол дифракции (при φ 0 sin φ φ),

m – порядок максимума или минимума,

λ – длина волны источник излучения, м.  = ...................................,м

Результаты вычисления записать в таблицу 2.

Таблица 2

№ щели
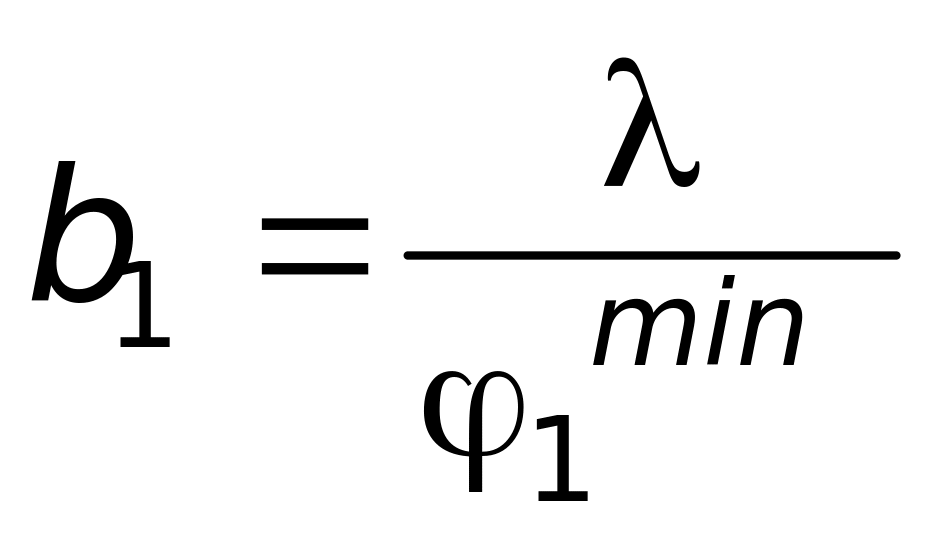
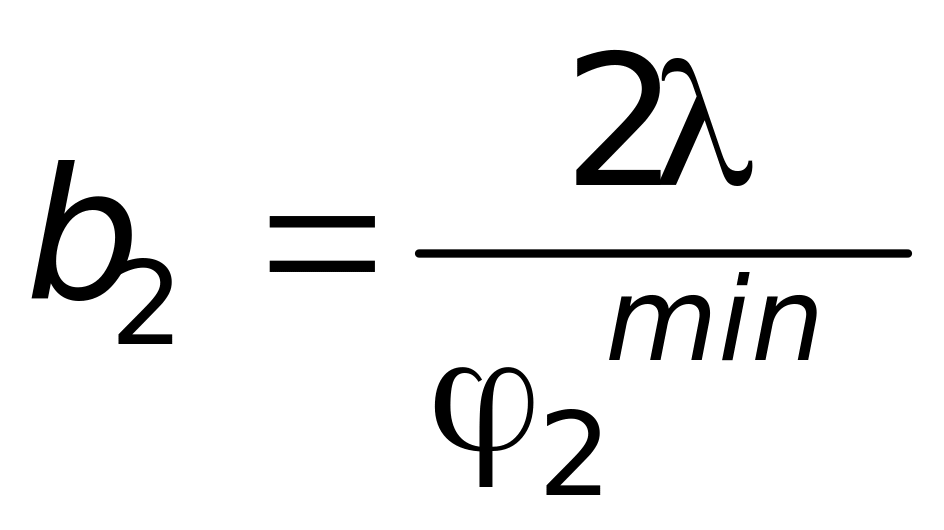
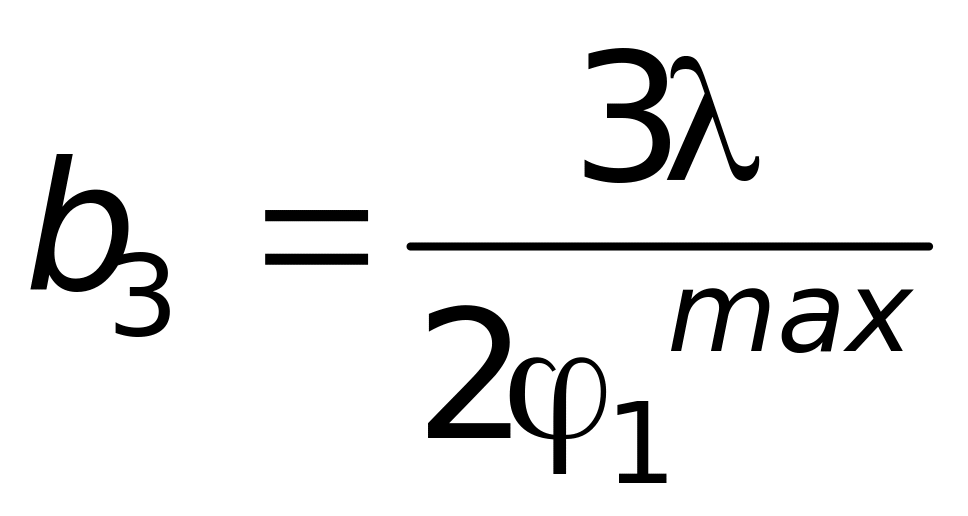
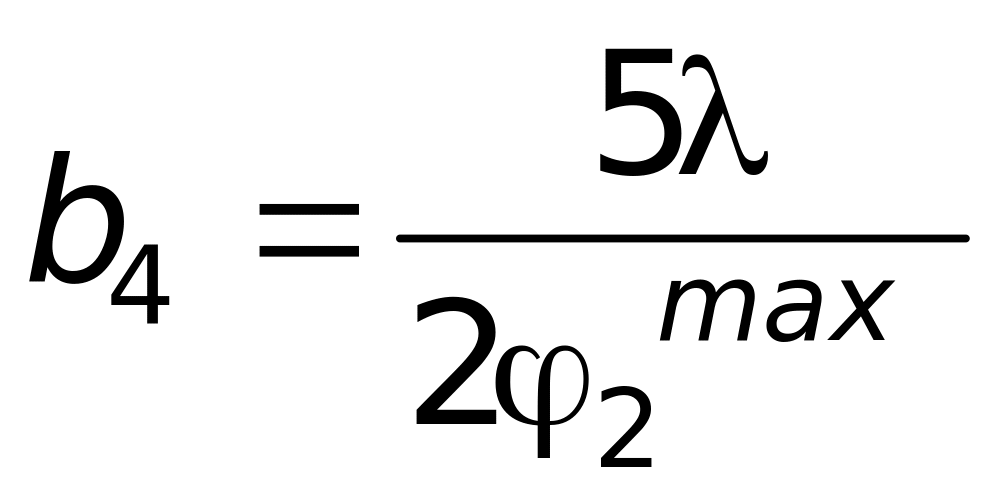
1
2
3
4
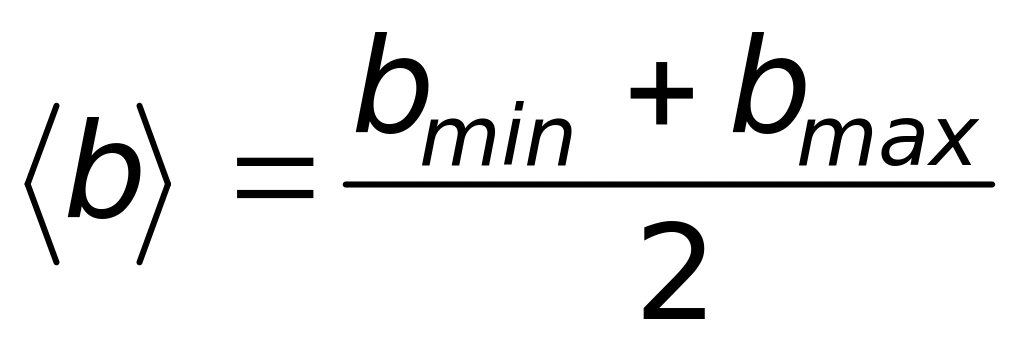
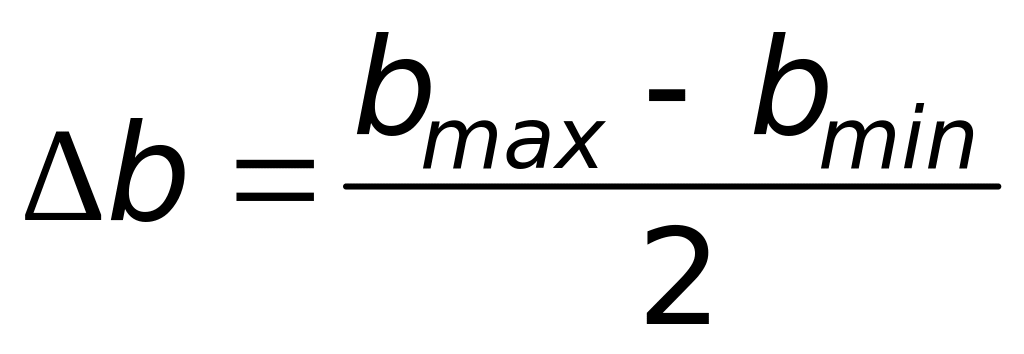
					bэксп = <b> ± Δb
1
2
3
4

По результатам таблиц 1,2 можно сделать вывод о влиянии ширины щели b на положение максимумов и минимумов в дифракционной картине. Кроме того, ширина щели b влияет на общую интенсивность (яркость) I света, прошедшего через щель.

Известно, что интенсивность света прямо пропорциональна квадрату амплитуды световой волны I ~ A². Таким образом, амплитуда световой волны А ~ .

Для каждой дифракционной картины соотношение амплитуд световой волны в максимумах имеет вид:

А₀: А₁: А₂ = 1: , где

А₀ – значение амплитуды в центральном максимуме («нулевой» порядок, m=0);

А₁ – значение амплитуды в первом максимуме, m=1,

А₂ – значение амплитуды во втором максимуме, m=2,

Все эти факторы необходимо учитывать для построения и анализа графиков зависимости амплитуды световой волны от угла дифракции φ_m или его синуса sin φ_m.

4.2.8. Рассчитать амплитуды световой волны в максимумах дифракционной картины по формуле (2):

Заполнить таблицу 3 для конкретных значений φ_m.

Таблица 3

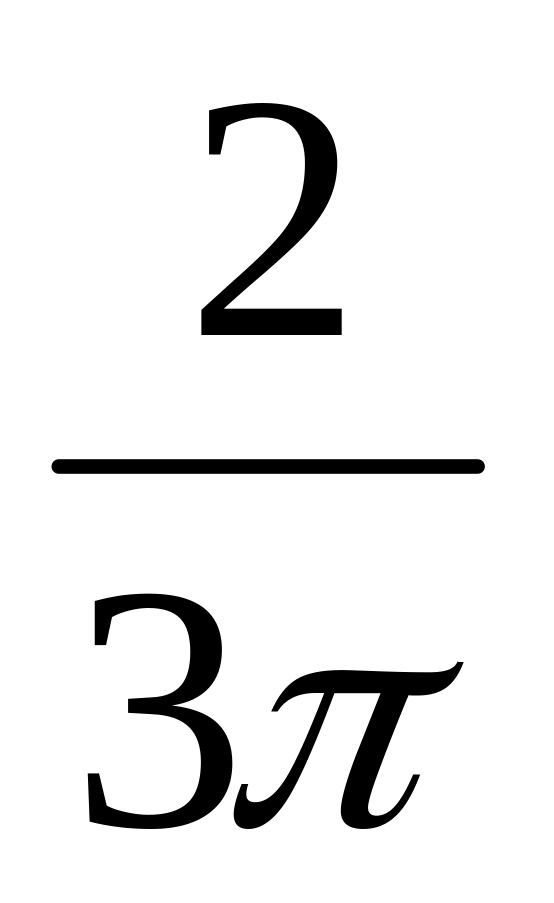
№ щели i	<bi>	A0i, φ = 0	A1i = A0i ·	± φ1max, рад
1
2
3
4
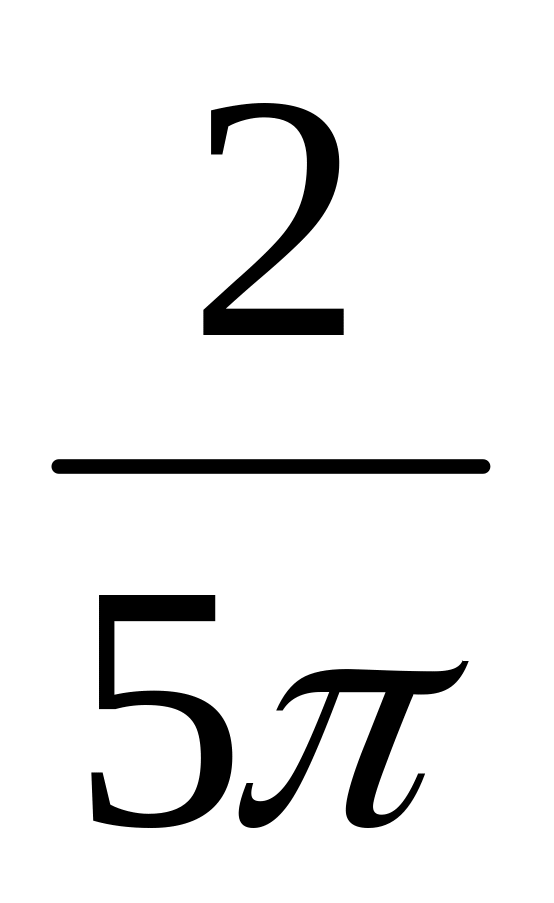
	A2i = A0i ·	± φ2max, рад	± φ1min, рад; A = 0	± φ2min, рад; A = 0
1
2
3
4

Принять А_o1 = 5 см, А_oi = 5 см , i=1,2,3.

4.2.9. По результатам таблицы 3 построить на одном листе миллиметровой бумаги три графика зависимости А = f (φ_m). Рекомендованный масштаб по оси абсцисс 0,05 рад : 5 см. Полученные экспериментальные точки соединить плавной кривой.