Лабораторная работа № 1 Изучение явления дифракции света

1. Цель работы

1.1. Наблюдение дифракционных картины от одной и двух щелей и круглого отверстия.

1.2. Установить влияние размера щели на дифракционную картину (при дифракции на одной щели).

1.3. Установить влияние размера щелей и расстояния между ними на дифракционную картину от двух щелей (опыт Юнга).

1.4. Установить влияние размеров круглого отверстия на вид дифракционной картины.

2. Приборы и принадлежности

2.1. Источник света – полупроводниковый лазер с длиной волны излучения λ = 650 нм.

2.2. Фотолитографический тест-объект (Т-О) с непрозрачным покрытием, на которое по трем различным окружностям нанесены:

внешняя окружность А – двойные щели;

окружность В – круглые отверстия;

окружность С –одинарные щели.

Диаметры круглых отверстий:

d₁ = 30мкм;

d₂ = 40мкм;

d₃ = 50мкм;

d₄ = 60мкм;

d₅ = 70мкм;

d₆ = 80мкм;

d₇ = 90мкм;

d₈ = 100мкм;

Тест-объект

2.3.Экран.

3. Краткое теоретическое введение

Дифракцией света принято называть отклонение света от его прямолинейного распространения и проникновение его в область геометрической тени.

При прохождении света через небольшие отверстия или узкие щели в результате дифракции на удаленном экране вместо изображения этих отверстий или щелей наблюдается чередование темных и светлых участков, соответствующих минимумам и максимумам интенсивности света. Похожие картины наблюдаются и при интерференции света.

Нахождение интенсивности света в интересующих точках пространства и является дифракционной задачей. В основе решения этой задачи лежит принцип Гюйгенса – Френеля: каждая точка волновой поверхности является источником вторичных когерентных волн.

Когерентными волнами называются волны, разность фаз которых не изменяется во времени. Волновой поверхностью называется геометрическое место точек, в которых фазы распространяющейся волны равны.

В дальнейшем этот принцип подтвердился электромагнитной теорией Максвелла.

В общем случае расчет дифракционной картины сводится к определению распределения интенсивности на экране при интерференции света от многих когерентных источников волновой поверхности, что приводит к громоздкому интегрированию.

Однако в случае симметричной задачи (прохождение света через круглое отверстие, щель, дифракционную решетку) расчет дифракции можно производить методом графического сложения (метод векторных диаграмм).

Различают два типа дифракции: дифракция света в сходящихся лучах от вторичных источников (дифракция Френеля) и дифракция света в параллельных лучах от вторичных источников (дифракция Фраунгофера).

Принципиального отличия дифракции Френеля от дифракции Фраунгофера нет.

Критерием этого отличия служит отношение ,

где d – размеры отверстия или щели;

l – расстояние от отверстия до точки наблюдения;

 - длина волны падающего света.

Если , то дифракция не наблюдается (геометрическая оптика).

Если , то это дифракция Фраунгофера.

Если , то это дифракция Френеля.

Рассмотрим дифракцию света на круглом отверстии и узкой щели.

Дифракция Френеля на круглом отверстии

Пусть свет с длиной волны  от точечного источника проходит через круглое отверстие малых размеров и попадает на экран.

Расстояние от точечного источника до отверстия – а, расстояние от отверстия до экрана – l, радиус отверстия - r. Величина а будет являться радиусом кривизны волнового фронта.

Вид наблюдаемой дифракционной картины будет зависеть от этих параметров.

Зафиксируем расстояния а и b, и рассмотрим, как будет меняться вид дифракционной картины с изменением радиуса отверстия r. При малых размерах r в центре картины будет наблюдаться максимум, и интенсивность света будет монотонно спадать в радиальном направлении (рис. 1). По мере увеличения радиуса отверстия интенсивность максимума будет возрастать и достигнет максимального значения при (рис. 2). При дальнейшем увеличении r интенсивность в максимуме начнет спадать, а распределение интенсивности в радиальном направлении примет вид изображенный на рис. 3. При значении интенсивность в центре картины будет минимальной (рис. 4). На рисунках 5 и 6 изображено распределение интенсивности при дальнейшем росте r. Рисунок 5 соответствует значению , рисунок 6 соответствует значению .

Радиус m-ой кольцевой зоны Френеля определяется выражением:

(1)

Если на отверстии укладывается нечетное число зон Френеля (1,3,5 и т.д.), то в центре дифракционной картины наблюдается максимум. Если на отверстии укладывается четное число зон Френеля (2,4,6 и т.д.), то в центре дифракционной картины наблюдается минимум.

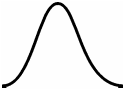
рис. 1 рис. 2 рис. 3

(менее 1 зоны Френеля) (1 зона Френеля) (1,5 зоны Френеля)

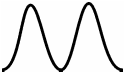
рис. 4 рис. 5 рис. 6

(2 зоны Френеля) (3 зоны Френеля) (4 зоны Френеля)

Если фронт падающей волны плоский а , то радиус m-ой кольцевой зоны Френеля определяется выражением: