Расчет статически неопределимых систем

2А. Расчет статически неопределимой балки (рис.2.1)

Требуется:

1. Раскрыть статическую неопределимость.

2. Построить эпюры Q и M.

Исходные данные

Таблица 2.1

Группа	a, м	b, м	c, м	F, кН	М, кНм	q, кН/м
1	2	2	4	50	10	8
2	1	3	5	40	20	6
3	4	2	3	30	30	14
4	2	1	4	20	40	10
5	3	4	2	10	50	20

2Б. Расчет статически неопределимой рамы методом сил (рис.2.2)

Требуется:

Для заданной рамы построить эпюры: изгибающих моментов, поперечных и продольных сил.

Исходные данные

Таблица 2.2

Группа	l, м	h, м	F, кН	q, кН/м	М, кНм	I1 :I2
1	1	3	10	12	20	2:1
2	2	2	20	10	30	1:2
3	3	1	30	8	15	1:3
4	4	2	40	6	25	3:1
5	6	3	50	4	10	3:2

Ход решения задачи [6]:

1. Определить степень статической неопределимости.

2. Выбрать основную систему путем отбрасывания лишних связей.

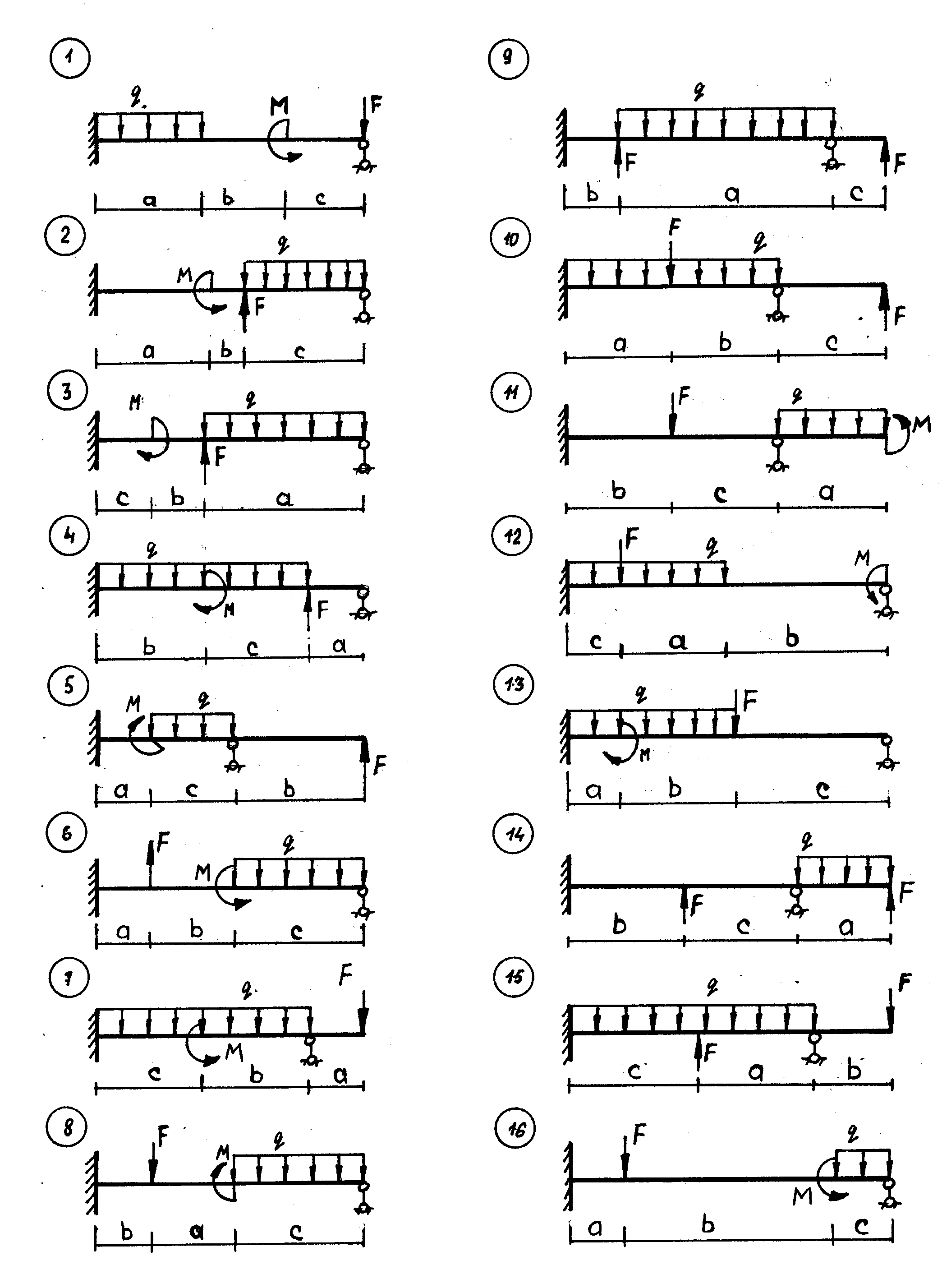
Рис.2.1.

Рис.2.1.

Рис.2.2.

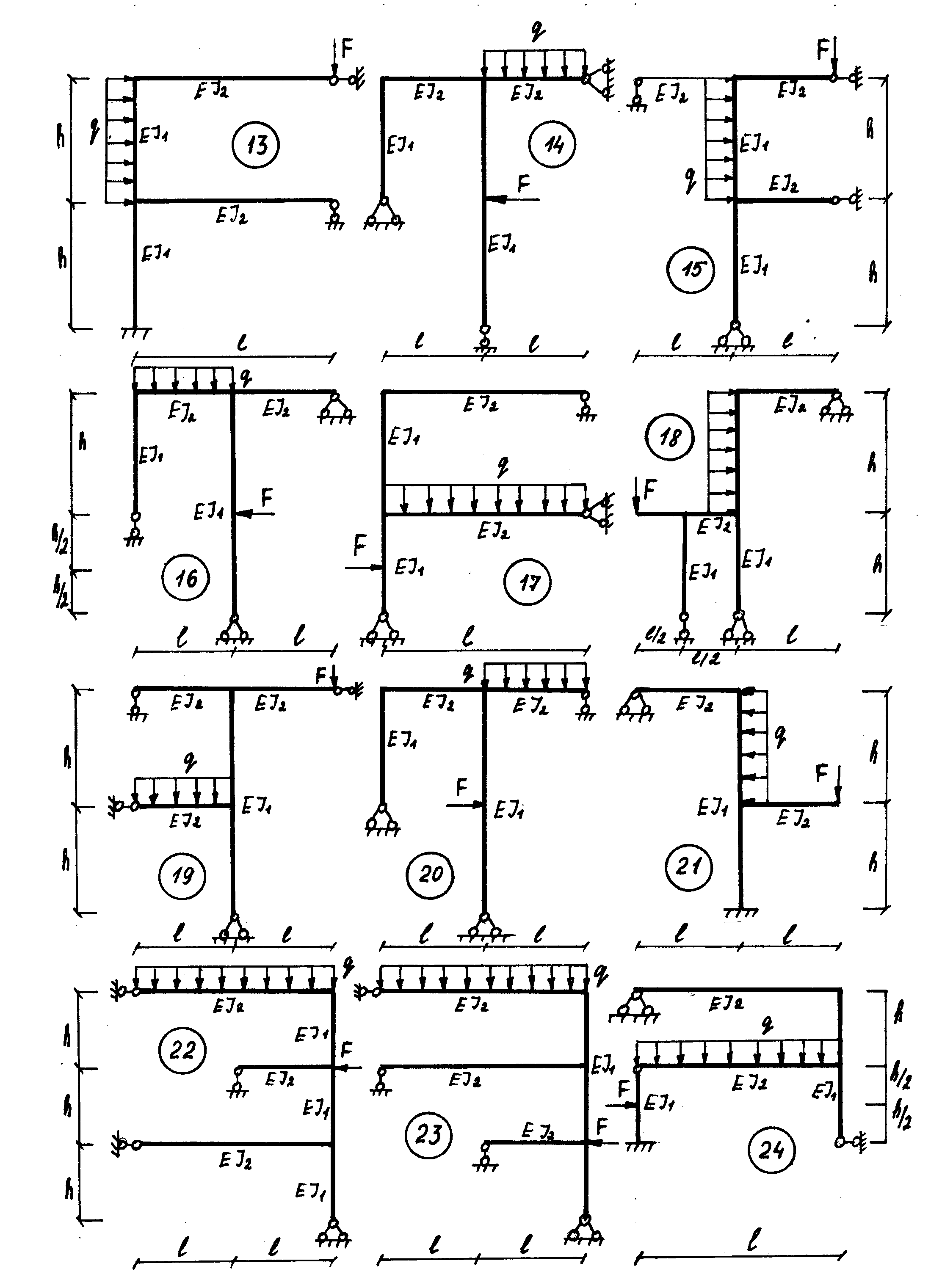
Рис.2.2.

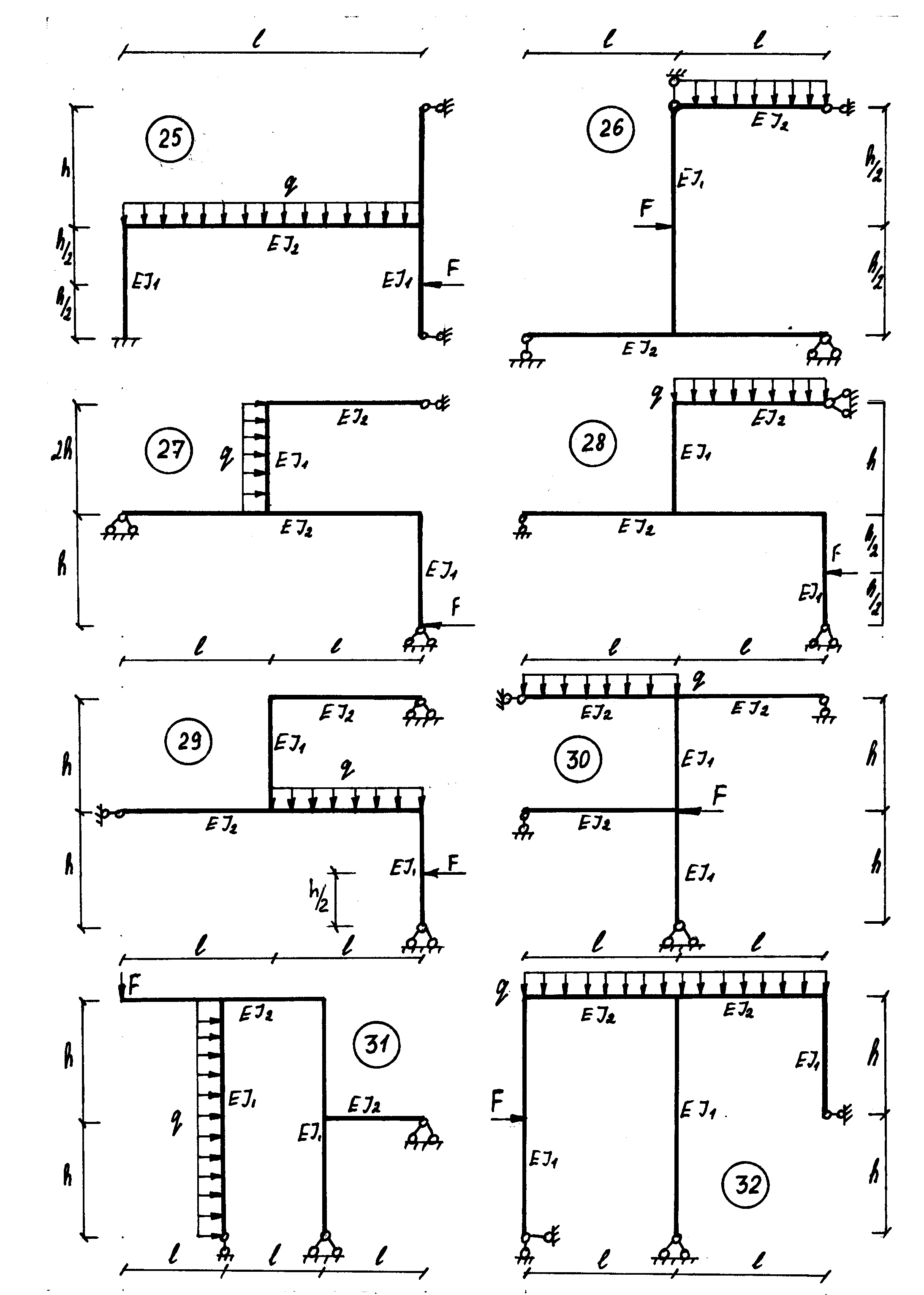
Рис.2.2.

3. Записать систему канонических уравнений:

4. Построить единичные эпюры изгибающих моментов для основной системы от действия соответственно .

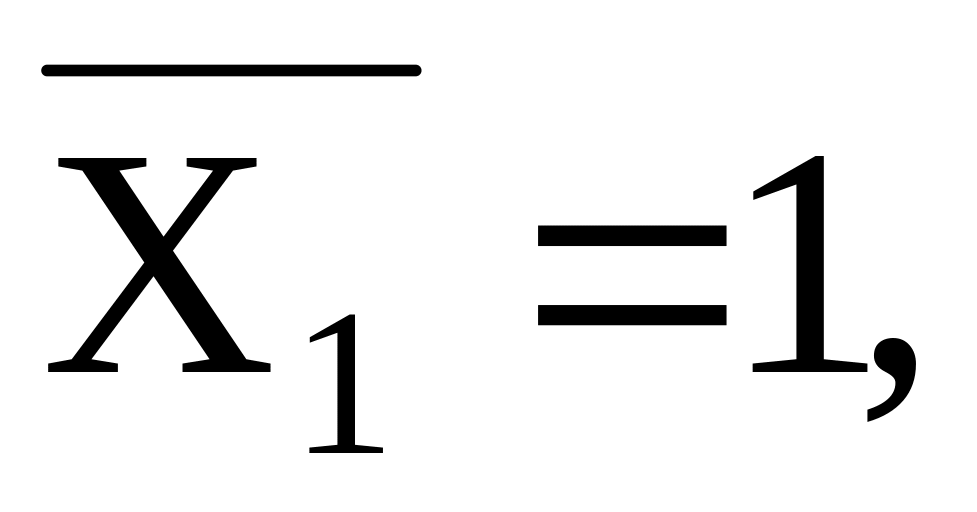
5. Построить эпюру изгибающих моментов для основной системы от заданных нагрузок.

6. Определить коэффициенты и свободные члены канонических уравнений и выполнить проверки.

7. Решить систему канонических уравнений метода сил.

8. Построить окончательную эпюру изгибающих моментов для заданной системы .

9. Выполнить статическую и деформационную проверку окончательной эпюры моментов.

10. Построить эпюры поперечных и продольных сил, используя зависимость:

и рассматривая уравнения равновесия для вырезанных узлов.

Работа №3

Балки на упругом основании

Для железобетонной балки (рис.3.1) прямоугольного сечения (b*h) требуется:

-построить эпюру реактивных давлений упругого основания.

-построить эпюру изгибающих моментов.

-построить эпюру поперечных сил.

Числовые данные:

Таблица 3.1

№ группы	Е, МПа	k|, кг/см3	b, м	h, м	L, м	q, кН/м	F, кН	M, кНм
1	24000	0.5	1	0.5	4	100	130	100
2	29000	0.55	1	0.52	6	120	200	140
3	34000	0.6	1	0.68	8	150	140	120
4	38000	0.65	1	0.72	10	40	70	80
5	15000	0.7	1	1	12	50	60	100

Схемы к работе:

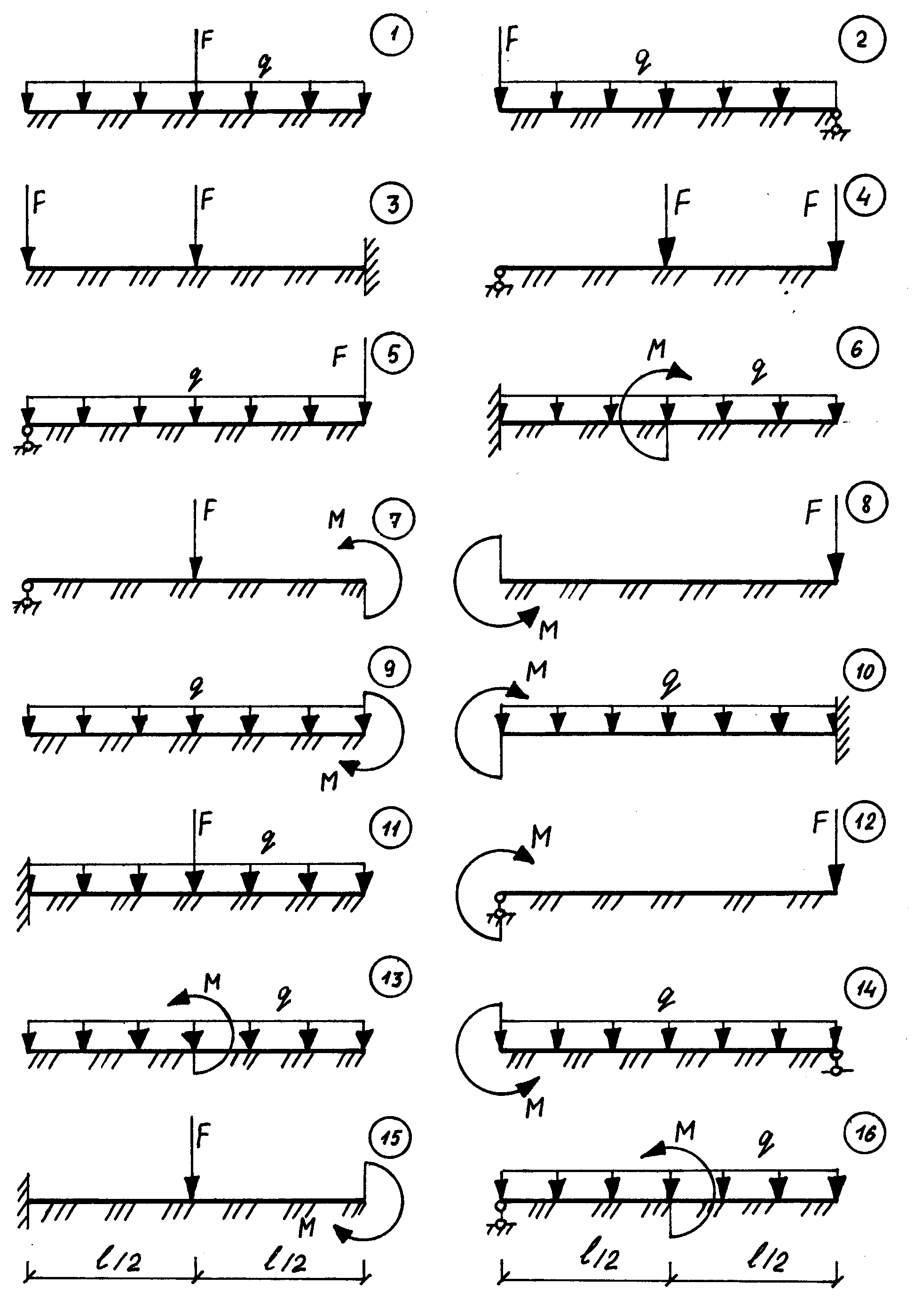
Рис.3.1.

Рис.3.1.

Ход решения задачи (методом начальных параметров)[1]:

1.Определить параметр .

2.Записать четыре аналитических выражения для заданной балки для .

3.Определить начальные параметры из условия закрепления балки. Два начальных параметра всегда известны исходя из закрепления балки в начале координат (крайняя левая точка). Два других находятся из системы двух уравнений, составленных для условий закрепления на другом конце балки.

4.Разбить балку на несколько участков (через 1 метр или 2 метра) и в каждом сечении определить M, Q, r. По результатам построить эпюры.