
- •Задачи на определение и использование коэффициентов теплоотдачи и массоотдачи в турбулентном потоке расплава (краткая теория).
- •Задача № 3. Определение скорости плавления холодильника.
- •1. Уравнение потока массы углерода в нашем случае описываем следующим образом:
- •2. Вычисляем поток углерода из жидкого чугуна в сталь
- •Задача № 4. Определение скорости плавления пластины.
- •По приведенному уравнению скорость плавления
- •Задача № 5. Определение коэффициента теплоотдачи по критерию Нуссельта.
- •Вычисляем критерий Нуссельта по формуле
- •Задача № 6. Определение коэффициента теплоотдачи по опытным данным.
Министерство образования и науки, молодёжи и спорта Украины
ГВУЗ «Приазовский государственный технический университет»
Кафедра
Технологии и компьютеризации литейного производства
Курсовая работа
по дисциплине
«Моделирование и оптимизация
технологических систем и процессов»
Студент гр. МЛ -08
Бабич Е. В.
Учебный год 2012
Семестр №7
Мариуполь, 2012 г.
Вариант 1-2
Задача 2.1. составление безразмерных комплексов подобия явлений по дифференциальным уравнениям.
Существует следующее правило составления выражения для безразмерных комплексов подобия из дифференциальных уравнений:
а) в дифференциальном уравнении необходимо отбросить все знаки дифференцирования, все индексы и символы (например, суммирования и др.); показатели степеней чисел отбрасывать нельзя;
б) полученное выражение разделить, на один из его членов и таким образом получить безразмерные комплексы;
в) используя размерности величин, убедиться в том, что полученные комплексы являются безразмерными.
Уравнение 1.
Дифференциальное уравнение распространения
тепла вдоль оси
 имеет вид
имеет вид
 , (1)
, (1)
где:
 - температура, 0С;
- температура, 0С;
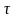 -
время, с;
-
время, с;
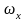 - скорость перемещения источника тепла
вдоль оси
- скорость перемещения источника тепла
вдоль оси
 ,
см/с;
,
см/с;
 - коэффициент
температуропроводности металла, см2/с.
- коэффициент
температуропроводности металла, см2/с.
Вариант 2. Все члены уравнения (1) после отбрасывания индексов и символов делить на второй член уравнения (1).
а) В уравнении (1) отбрасываем все индексы и символы, тогда получим:
 (1а)
(1а)
б) Делим (1а) на второй член уравнения:
 ; (1б)
; (1б)
После необходимых сокращений получим:
 ;
(1в)
;
(1в)
в) проверим безразмерность
полученных критериев
 и
и
 :
:
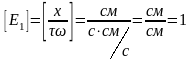 ;
;
 .
.
Ответы: ; .
Задачи на определение и использование коэффициентов теплоотдачи и массоотдачи в турбулентном потоке расплава (краткая теория).
Процессы передачи тепла и вещества в турбулентном потоке жидкости весьма сложны и описываются, чаще всего с помощью эмпирических уравнений.
Для процесса теплопередачи от поверхности твердого тела к жидкости и наоборот справедливо уравнение
 (2)
(2)
где  – тепловой поток:
– тепловой поток:
 – разность температур между более
нагретой и более холодной частью тела;
– разность температур между более
нагретой и более холодной частью тела;
- коэффициент пропорциональности между тепловым потоком и разностью температур; он носит название коэффициента теплоотдачи.
Аналогично, для процессов переноса вещества при растворении твердого в жидкости за счет изменения химического состава твердого и жидкого справедливо уравнение
 (3)
(3)
где  – поток массы от жидкого к твердому;
– поток массы от жидкого к твердому;
C2 – C1 – концентрация компонентов раствора в жидком и твердом состоянии (например углерода в жидком чугуне и твердой стали)
- коэффициент массоотдачи.
Процессы массопереноса в литейном производстве наблюдаются при плавлении твердой стали в жидком чугуне. В этом случае углерод из жидкого чугуна (температура 1200 – 13000С) диффундирует в поверхностный слой стали (температура плавления 1400 – 15000С), насыщает ее поверхность углеродом и понижает температуру плавления.
Коэффициенты и определяются либо непосредственно опытным путем, либо вычисляются с помощью теории подобия явлений.
Эти коэффициенты входят в выражения критериев Нуссельта: Nu теплового:
 (4)
(4)
диффузионного:
 (5)
(5)
где d – характерный размер тела;
- коэффициент теплопроводности тела;
D – коэффициент диффузии вещества в жидкости вблизи границы твердого
В теории подобия известны зависимости вида
 (6)
(6)
для вынужденного турбулентного потока жидкости или зависимости вида
 (7)
(7)
для естественной конвекции жидкости в турбулентном потоке. В уравнениях (6) и (7) характер потока жидкости определяется критериями Рейнольдса Re и Грасгофа Gr, а свойства самой жидкости критерием Прандтля Pr.
Ниже на конкретных
примерах рассмотрены способы определения
коэффициента теплоотдачи
 и коэффициента массоотдачи
и коэффициента массоотдачи
 .
.
Задача № 3. Определение скорости плавления холодильника.
В форму помещен холодильник из малоуглеродистой стали, форму заливают чугуном с высоким содержанием углерода. Найти линейную скорость плавления плоского холодильника если задан коэффициент массоотдочи , массовое содержание углерода в стальном холодильнике Сх и чугуне Сч, % мас. Плавление холодильника происходит после насыщения поверхности стального лома до содержания углерода, соответствующего температуре ликвидус сплава Cл.
Решение.
Вариант |
Содержание углерода, %масс. |
β, см/с |
|||
СЧ |
СХ |
СЛ |
|||
16 |
4,5 |
0,17 |
2,2 |
0,20 |
|
1. Уравнение потока массы углерода в нашем случае описываем следующим образом:

где Сч и Сл – необходимо выразить в граммах углерода на
1 см3 металла (обозначим Суг).
Принимаем плотность стали с = 7,5 г/см3
а) Содержание углерода в чугуне
 г/см3;
г/см3;
б) Содержание углерода, соответствующее ликвидусу сплава:
 г/см3;
г/см3;
