Поле однородно заряженного бесконечного цилиндра.

(Рисунок)

,

r > R,

,

(Рисунки)

Для цилиндрической оболочки поле внутри отсутствует.

лекция 3

характеристики электростатич поля

потенциал

теорема стокса

уравнения электростатич поля

Ротор. Теорема Стокса.

Если в движущеёся жидкости с распределением скоростей от до выделить контур Г, а остальную жидкость мгновенно заморозить, то в этом контуре будет продолжаться движение жидкости. Мерой такого действия является произведение скорости жидкости в контуре на длину контура. Эту величину называют циркуляцией вектора по контуру Г.

Циркуляция =

Циркуляция обладает свойством аддитивности, т.е. циркуляция по контуру Г будет равна сумме циркуляций по контурам Г₁ и Г_2.

Благодаря такому свойству можно ввести понятие удельной циркуляции в точке Р – это векторная величина, называемая ротором или вихрем.

Рассмотрим циркуляцию по элементарному квадрату в декартовой системе координат.

Знак минус ставится тогда, когда направления c_x не совпадает с направлением обхода.

Учитывая, что , получим:

Аналогично для сторон квадрата 2 и 4:

,

Тогда циркуляция по квадрату будет равна:

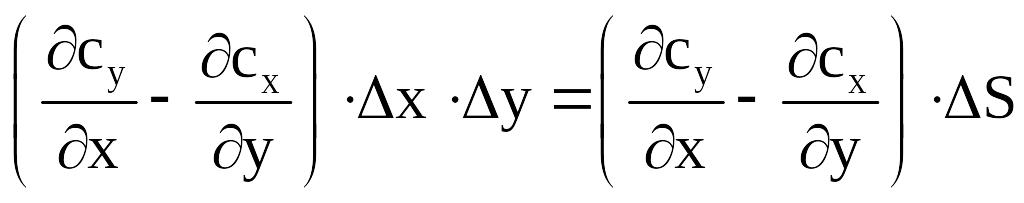, где S – площадь квадрата.

Разделив циркуляцию на , найдём проекции на оси координат:

(1*)

(2*)

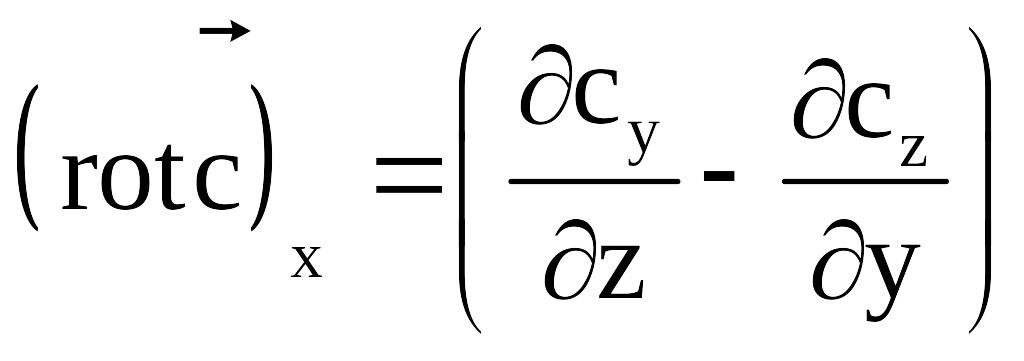(3*)

Любое из выражений (1*) - (3*) можно получить из предыдущего путём циклической системы координат.

Для уравнения (1*) предыдущим является уравнение (3*). Таким образом, ротор вектора в декартовой системе координат будет иметь вид:

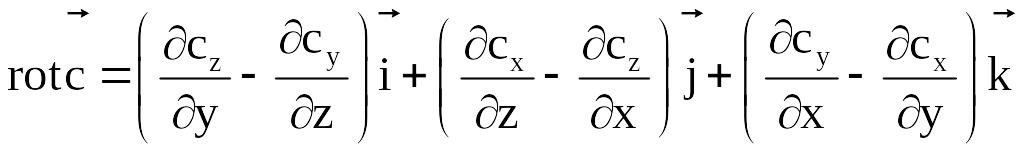
Если известно, что ротор каждой точки поверхности S охватывается контуром Г, то можно вычислить и циркуляцию по этому контуру:

Теорема Стокса: циркуляция вектора по замкнутому контуру равна потоку вектора rot через площадку S, ограниченную этим контуром.

Отметим, что

Мы рассмотрим три вида сочетаний, в которые входит оператор (набла)

_{(векторное произведение)}

Используя эти сочетания, можно пространственные вариации полей записать в виде независимых от той или иной совокупности осей координат.

Формула Стокса.

По определению ротор (вихрь) некоторого вектора :

(36)

Зная ротор вектора в каждой точке некоторой (не обязательно плоской) поверхности S, можно вычислить циркуляцию этого вектора по контуру , ограничивающему S, (контур также может быть не плоским). Для этого разобъём поверхность на очень малые элементы . Ввиду их малости эти элементы можно считать плоскими. Поэтому в соответствии с (36) циркуляция вектора по контуру, ограничивающему , может быть представлена в виде.

(37)

где - положительная нормаль к элементу поверхности .

Зная, что циркуляция по некоторому контуру равна сумме циркуляций по контурам, содержащиеся в данном, можно просуммировать выражение (37) по всем , и тогда получим циркуляцию вектора по контуру , ограничивающему S:

.

Осуществив предельный переход, при котором все стремиться к нулю (число их при этом неограниченно растёт, придём к формуле:

(38)

Соотношение (38) носит название теоремы Стокса. Смысл её состоит в том, что циркуляция вектора по произвольному контуру равна потоку вектора через произвольную поверхность S , ограниченную данным контуром.