2.2. Показатели центра распределения

Средняя арифметическая взвешенная:

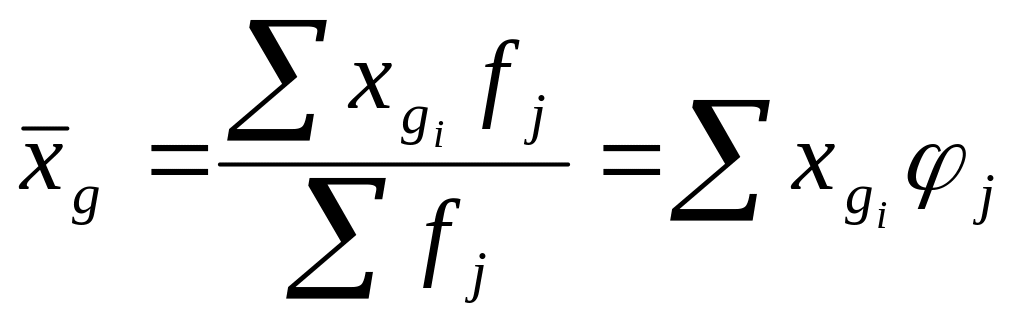, (16)

где - значения j-ой середины интервалов;

- частости j-го интервала.

В связи с тем, что в Excel отсутствует формула для вычисления средней арифметической взвешенной в ячейку В84 запишем выражение = СУММПРОИЗВ (V3:V7;X3:X7).

Мода и медиана относятся к структурным средним. Их значения находятся из выражений:

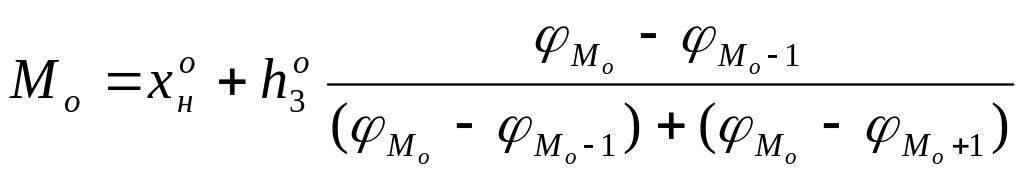(17)

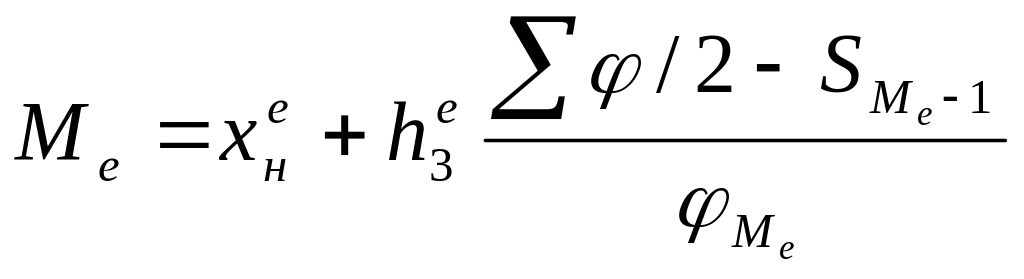(18)

где - нижние границы модального и медианного интервалов;

- ширина модального и медианного интервалов;

- частость модального интервала;

- частость интервала, предшествующему модальному;

- частость интервала следующего за модальным;

- половина суммы накопленных частостей (равна 0,5);

- накопленная частость до медианного интервала;

- частость медианного интервала.

Формулы (15,16 и17) записаны в ячейках B84,В85 и В86 соответственно.

В первом пункте задания сделан вывод о правосторонней асимметрии, а по сгруппированным данным получается, что асимметрия левосторонняя, т.к. .

Противоречие объясняется некоторым произволом в выборе количества групп. Для каждой из 4-х представленных на рис. 5,6, 7, 9 диаграммах будут свои значения , отличающиеся друг от друга. Если существует возможность вычислить значения по не сгруппированным данным, то ее необходимо использовать.

2.3. Показатели вариации

1. Размах вариации (формула 15, ячейка В76).

2. Среднее линейное отклонение (ячейка В87):

. (19)

3. Дисперсия (ячейка В88):

. (20)

4. Среднее квадратическое отклонение (ячейка В89):

. (21)

5. Коэффициент осцилляции (ячейка В90):

. (22)

6. Линейный коэффициент вариации (ячейка В91):

. (23)

7. Коэффициент вариации (ячейка В92):

. (24)

8. Относительный показатель квартильной вариации (ячейка В93):

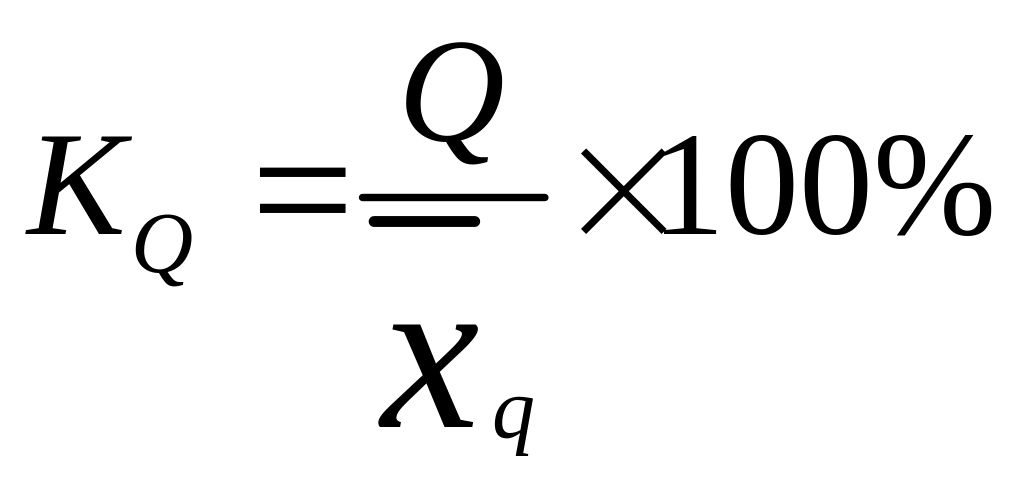, (25) где - среднее квартильное расстояние;

;

;

- соответственно первая и третья квартили распределения;

- нижние границы интервалов, в которых находятся первая и третья квартили;

- ширины интервалов первой и третьей квартили;

и - сумма накопленных частостей в интервалах предшествующих интервалам, в которых находятся первая и третья квартили;

- частости интервалов, в которых находятся первая и третья квартиль.

В практике из показателей вариации получили широкое применение дисперсия, среднее квадратическое отклонение и коэффициент вариации.

2.4. Показатели дифференциации

1. Коэффициент фондовой дифференциации

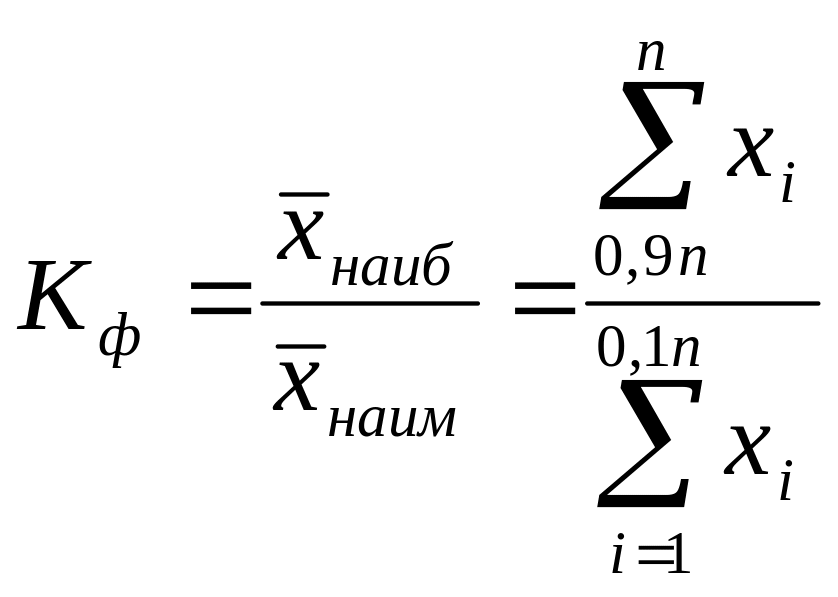, (26)

где - средние значения для 10% банков с наибольшими и для 10% с наименьшими значениями активов.

Формула (26) реализована в ячейке В94. Средние значения активов «богатых» банков превышают средние значения активов «бедных» в 1,5 раза.

2. Коэффициент децильной дифференциации

, (27)

где - максимальное значение активов у 10% банков с наименьшими активами;

- минимальное значение активов у 10% банков с наибольшими активами;

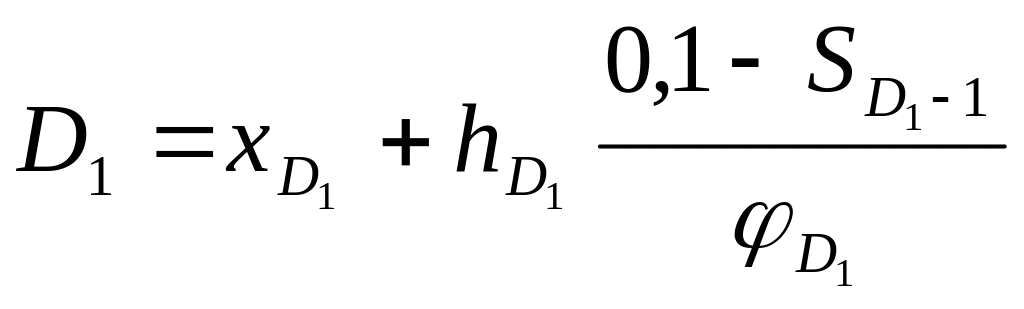; (28)

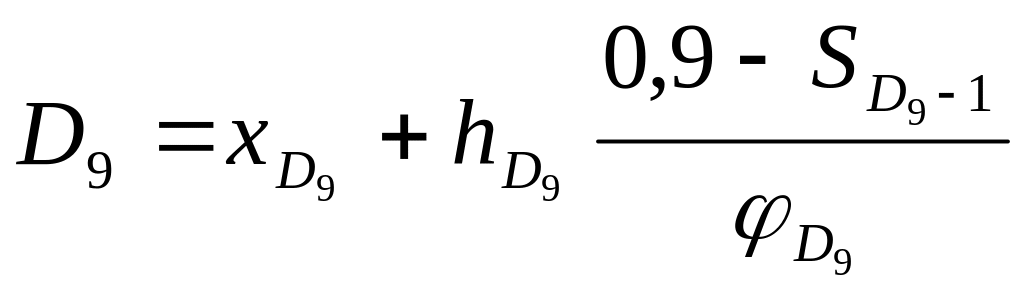; (29)

- нижние границы интервалов, в которых находятся первая и девятая децили;

- ширины интервалов первой и девятой децили;

- сумма накопленных частостей в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили;

- частости интервалов, в которых находятся первая и девятая децили.

Выражения (27-29) реализованы в ячейке В95. Из двух показателей предпочтение следует отдать коэффициенту фондовой дифференциации. Его значение более устойчиво (при соблюдении правил округления) по сравнению с коэффициентом децильной дифференциации, зависящего от количества групп в структурной группировке. Кроме того, оба показателя являются ненормированными. Вследствие этого одно и тоже значение каждого из них можно толковать по-разному. Для устранения указанной неопределенности условимся вычислять значения и по формулам:

Оценку степени дифференциации можно осуществить по шкале Чеддока.

Степени дифференциации	Значение коэффициентов
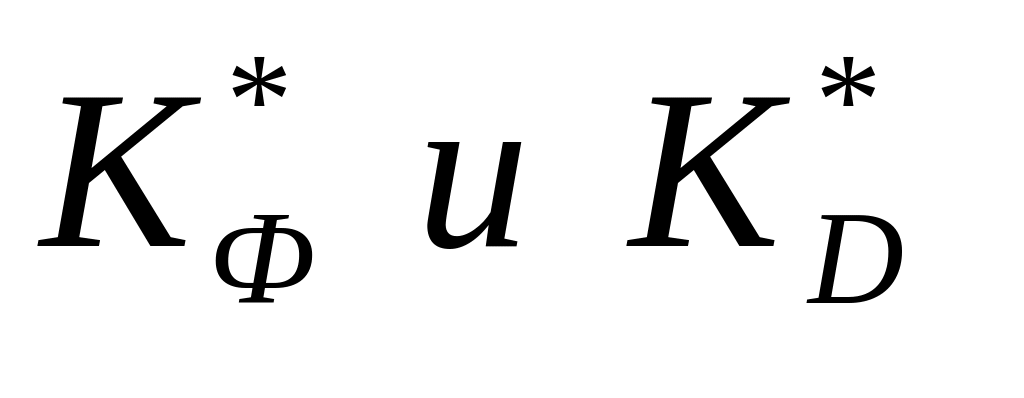
Слабая	0,1 – 0,3
Умеренная	0,3 – 0,5
Заметная	0,5 – 0,7
Высокая	0,7 – 0,9
Весьма высокая	0,9 – 0,99

Учитывая, что расчетное значение , степень дифференциации банков по стоимости активов является слабой.