
- •5.1.2. Собственная проводимость полупроводников
- •5.1.3.Электропроводность примесных полупроводников
- •5.1.4.Элементарная теория электропроводности полупроводников
- •5.1.5.Зависимость проводимости полупроводника от температуры
- •5.2.Электропроводность металлов. Зависимость электропроводности металлов от температуры
- •5.3. Эффект холла
5.1.4.Элементарная теория электропроводности полупроводников
Проведём расчет плотности тока для донорного полупроводника.
Концентрация
электронов
![]() ,
скорость дрейфового движения
,
скорость дрейфового движения
![]() .
.
Плотность тока – это заряд, проходящий за единицу времени через единичное сечение площадки, перпендикулярно скорости движения, т.е.
![]() .
.
Пусть
![]() - вероятность
того, что электрон за время
- вероятность
того, что электрон за время
![]() испытает
столкновение
(рассеяние).
испытает
столкновение
(рассеяние).
Вероятность
столкновения в единицу времени
![]() не зависит от времени, т.е.
не зависит от времени, т.е.
![]() .
Количество
столкновений для
частиц за время
равно
.
Количество
столкновений для
частиц за время
равно
![]() ,
т.е. за время
,
т.е. за время
концентрация
носителей заряда, движущихся в заданном
направлении, уменьшается в результате
рассеяния на
![]() .
.
Решив это уравнение относительно , получаем
количество
электронов, не испытавших за время
соударения:
![]() ,
,
![]() при t
= 0.
при t
= 0.
Внешнее электрическое
поле напряженностью
![]() сообщает
электрону ускорение
сообщает
электрону ускорение
![]() за
время свободного пробега
электрон приобретает дрейфовую скорость
за
время свободного пробега
электрон приобретает дрейфовую скорость
![]() и
пройдет путь
и
пройдет путь
![]()
Расстояние, которое пройдут все электроны в направлении поля
![]()
Если
![]() электронов имеют среднее время пробега
электронов имеют среднее время пробега
![]() ,
,
то время движения
всех электронов
![]() .
.
Есть определенная
вероятность того, что среди электронов
имеются такие, которые обладают одним
и тем же временем свободного пробега
.
Это электроны, испытавшие соударение
в момент времени от
![]() до
до
![]() .
.
Количество таких
электронов
,
время их движения
и вероятность столкновения
![]() .
Интегрируя это выражение по всем временам
свободного пробега от 0 до
.
Интегрируя это выражение по всем временам
свободного пробега от 0 до
![]() ,
,
найдем время
движения электронов:
![]()
Среднее время
свободного пробега
![]() .
.
Таким образом,
![]() - это среднее
время свободного пробега,
т.е. среднее время движения электронов
между двумя соударениями,
- это среднее
время свободного пробега,
т.е. среднее время движения электронов
между двумя соударениями,
тогда скорость
дрейфа электронов
![]()
пропорциональна напряженности электрического поля, времени свободного пробега и обратно пропорциональна массе электрона.
Параметр,
связывающий дрейфовую скорость носителей
заряда с напряженностью электрического
поля, называют
подвижностью
носителей
![]() .
.
Тогда
![]() и
и
![]() - подвижность численно равна скорости
дрейфа в электрическом поле единичной
напряженности.
- подвижность численно равна скорости
дрейфа в электрическом поле единичной
напряженности.
С учетом сказанного
![]() .
.
По закону Ома
![]() , тогда удельная проводимость равна
, тогда удельная проводимость равна
![]()
5.1.5.Зависимость проводимости полупроводника от температуры
Зависимость проводимости полупроводника от температуры определяется температурной зависимостью концентрации и подвижности носителей в полупроводнике.
Подвижность
показывает, какую скорость
![]() приобретает
носитель заряда под действием единичной
напряженности
электрического поля.
приобретает
носитель заряда под действием единичной
напряженности
электрического поля.
В примесных
полупроводниках носители заряда
рассеиваются не только на фононах
(тепловое рассеяние), но и на ионизированных
атомах примеси. Расчеты показывают, что
подвижность, обусловленная рассеянием
на ионизированной примеси, в случае
невырожденного электронного газа
пропорциональна
![]() ,
а в случае вырожденного газа она не
зависит от температуры. Этот механизм
рассеяния играет решающую роль при
низких температурах, когда концентрация
фононов мала. При высоких температурах
доминирует рассеяние на фононах–
тепловое рассеяние.
,
а в случае вырожденного газа она не
зависит от температуры. Этот механизм
рассеяния играет решающую роль при
низких температурах, когда концентрация
фононов мала. При высоких температурах
доминирует рассеяние на фононах–
тепловое рассеяние.
р ис.5.8
Зависимость
подвижности от температуры для примесного
невырожденного полупроводника,
учитывающая как рассеяние на ионах, так
и рассеяние на фононах.
ис.5.8
Зависимость
подвижности от температуры для примесного
невырожденного полупроводника,
учитывающая как рассеяние на ионах, так
и рассеяние на фононах.
При наличии обоих
механизмов рассеяния результирующая
подвижность
![]() определяется
выражением
определяется
выражением![]()
где
![]() - подвижность
носителей заряда при рассеянии только
на примесях,
- подвижность
носителей заряда при рассеянии только
на примесях,
![]() - только
на тепловых колебаниях.
- только
на тепловых колебаниях.
При этом
![]()
![]() .
.
Поэтому![]() .
.
(рис.5.8).
преобладает
При низких температурах- первое слагаемое,
при высоких – второе
Положение максимума на кривой зависит от концентрации дефектов в решетке
– с увеличением концентрации дефектов максимум смещается в сторону более высоких температур.
На основании изложенного можно сделать вывод о том, какой должна быть температурная зависимость проводимости примесного полупроводника:
В интервале температур, где концентрация носителей экспоненциально зависит от температуры,
 также практически является экспоненциальной
функцией,
также практически является экспоненциальной
функцией,а в области истощения примеси ход кривой определяется подвижностью.
Таким образом, температурный ход проводимости полупроводника определяется в основном экспоненциальным множителем,
поэтому удельная
проводимость полупроводника![]()
где
![]()
![]() - собственная
и примесная удельные проводимости,
- собственная
и примесная удельные проводимости,
- ширина запрещенной зоны,
![]() - энергия,
необходимая для создания примесного
носителя заряда,
- энергия,
необходимая для создания примесного
носителя заряда,
![]() ,
,
![]() - коэффициенты,
зависящие от природы полупроводника.
- коэффициенты,
зависящие от природы полупроводника.
можно пренебречь
При низкой температуре первым слагаемым, и

при высоких температурах можно пренебречь вторым слагаемым, поэтому
![]() .
.
(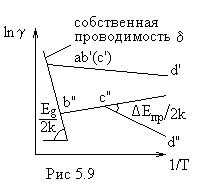 рис.5.9).
Температурную
зависимость полупроводника от температуры
удобно анализировать с помощью графика
в полулогарифмической системе координат.
рис.5.9).
Температурную
зависимость полупроводника от температуры
удобно анализировать с помощью графика
в полулогарифмической системе координат.
График имеет вид ломаной линии
участки
 В области
низких
температур
имеет место примесная
проводимость
которая растет с ростом температуры,
т.к. растет концентрация примесных
носителей заряда.
В области
низких
температур
имеет место примесная
проводимость
которая растет с ростом температуры,
т.к. растет концентрация примесных
носителей заряда.
Участки
 соответствуют
ситуации, когда атомы примеси
ионизированы, а собственная проводимость
ещё мала. За счет уменьшения подвижности
носителей с ростом температуры
проводимость полупроводника несколько
уменьшается. С дальнейшим ростом
температуры начинает преобладать
собственная проводимость.
соответствуют
ситуации, когда атомы примеси
ионизированы, а собственная проводимость
ещё мала. За счет уменьшения подвижности
носителей с ростом температуры
проводимость полупроводника несколько
уменьшается. С дальнейшим ростом
температуры начинает преобладать
собственная проводимость.С ростом концентрации примесей участки ломаной линии
 смещаются вверх, и температура перехода
от примесной проводимости к собственной
смещается в сторону более высоких
температур.
смещаются вверх, и температура перехода
от примесной проводимости к собственной
смещается в сторону более высоких
температур.
(участок
 ).
При больших
концентрациях примеси атомы примеси
остаются неполностью ионизированы
вплоть до температуры, при которой
начинается собственная проводимость
.
).
При больших
концентрациях примеси атомы примеси
остаются неполностью ионизированы
вплоть до температуры, при которой
начинается собственная проводимость
.
Экспериментально
доказано, что с
увеличением концентрации доноров (или
акцепторов) наклон прямых
![]() в области примесной проводимости
уменьшается.
в области примесной проводимости
уменьшается.
Это связано с уменьшением энергии ионизации примеси.
При некоторой
критической концентрации она обращается
в ноль. Для элементов пятой группы в
германии эта критическая концентрация
составляет
![]() см
см![]() ,
а в кремни
см
,
а в кремни
см![]() см.
см.
Полупроводник, в котором энергия ионизации примеси обращается в ноль, называют полуметаллом. В нем концентрация электронов и электропроводность нечувствительны к температуре (за исключением области, где начинается собственная проводимость).
График зависимости позволяет определить
ширину запрещенной зоны
и энергию ионизации примесных носителей .
