4.7. Термодинамическая диаграмма т – s и её применение

При изучении термодинамических процессов и некоторых общих вопросов термодинамики широко используется Т — S-диаграмма, в которой по осям абсцисс и ординат отложены соответственно энтропия S и термодинамическая температура Т рассматриваемого тела (системы).

Р ассмотрим некоторый обратимый процесс, который в этой диаграмме изображается линией DE (рис. ).

На диаграмме Т — S

- элементарная теплота изображается площадью, закрашенной на рисунке.

- количество теплоты , сообщаемое системе в процессе DE, пропорционально площади фигуры S_DDES_E (коэффициент пропорциональности зависит от выбора масштабов по осям координат) :

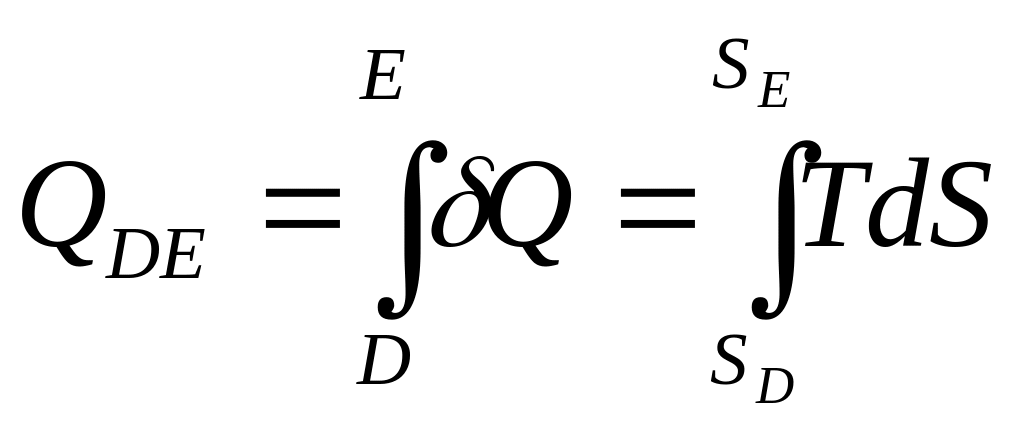
1) Cвязь между температурой и энтропией идеального газа в четырех простейших его процессах

Построим соответствующие им линии в Т — S-диаграмме.

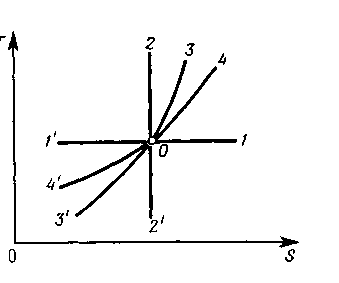Пусть

• точка О в диаграмме Т — S изображает начальное состояние идеального газа

• прямая 1 – 1^/ проходящая через точку О параллельно оси абсцисс, соответствует изотермическому процессу:

0—1 — изотермическое расширение (теплота подводится, так что dS>0),

0—1' - изотермическое сжатие (теплота отводится, так что dS<0).

• прямая 2'—2, проходящая через точку О параллельно оси ординат, изображает адиабатный (изоэнтропийный) процесс:

0—2— адиабатное сжатие (dТ>0)

0—2'—адиабатное расширение (dТ<0).

• линия 3'—3 - изохорный процесс е:

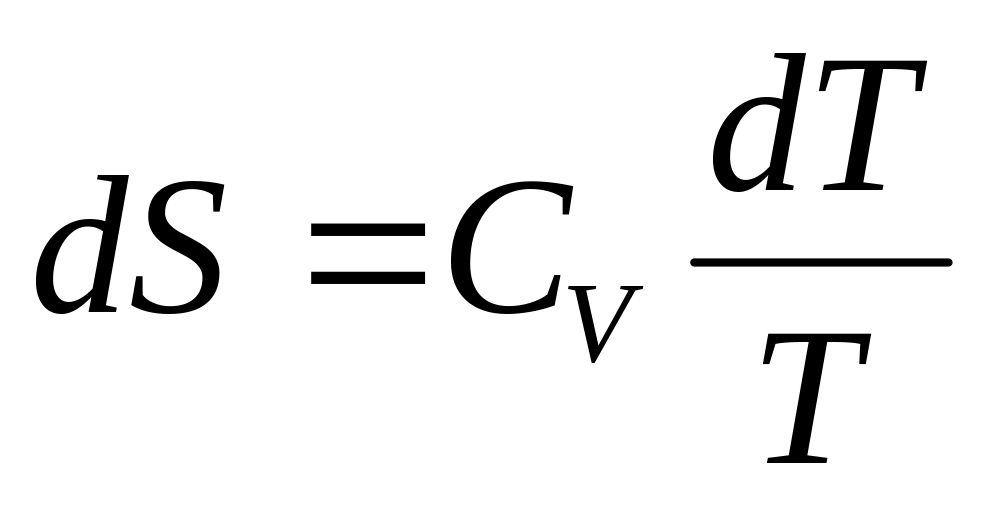
0—3 — изохорное нагревание (dS>0 и dТ>0),

0—3'—изохорное охлаждение (dS<0 и dТ<0).

в конечном изохорном процессе

• линией 4'—4 - изобарный процесс, так как , то изобарный процесс показан, идущей положе изохоры З'—З.

В изобарном процессе,

в конечном изобарном процессе

-изобарному расширению газа соответствует участок изобары 0—4 (dS>0 и dT>0),

- изобарному сжатию — участок 0—4' (dS<0 и dT<0).

2) На рисунке изображен в Т — S-диаграмме произвольный (обратимый!) прямой цикл abcda.

• С 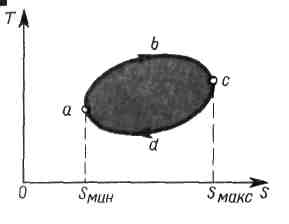остояния а и с соответствуют наименьшему (S_min) и наибольшему (S_max) значениям энтропии рабочего тела в цикле.

• в процессе аbс теплота подводится: >0

• в процессе cda — отводится: 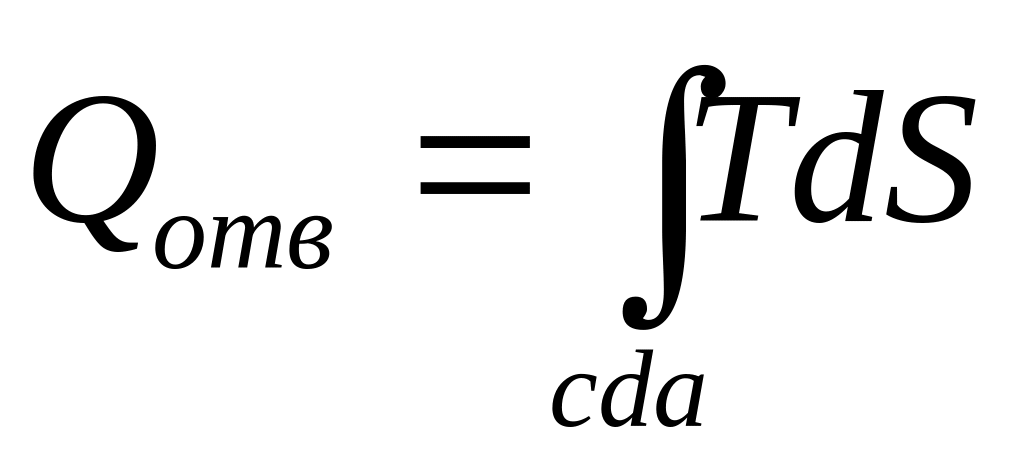<0.

• Работе за цикл А = 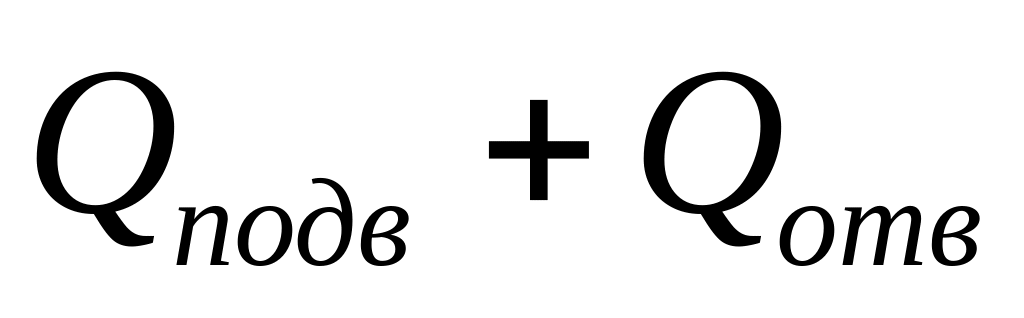соответствует площадь цикла, т. е. площадь, ограниченная замкнутой кривой abcda процесса: 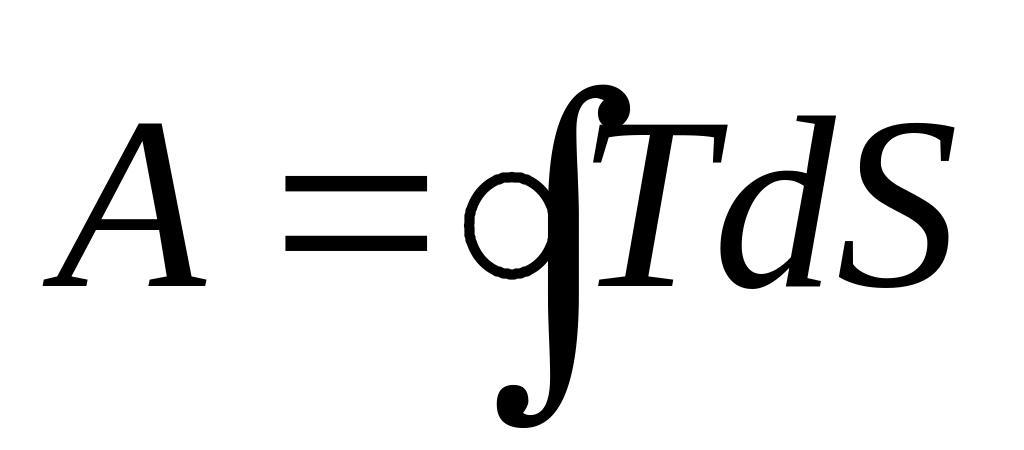>0

• Термическому КПД цикла соответствует отношение площади цикла к площади под кривой abc

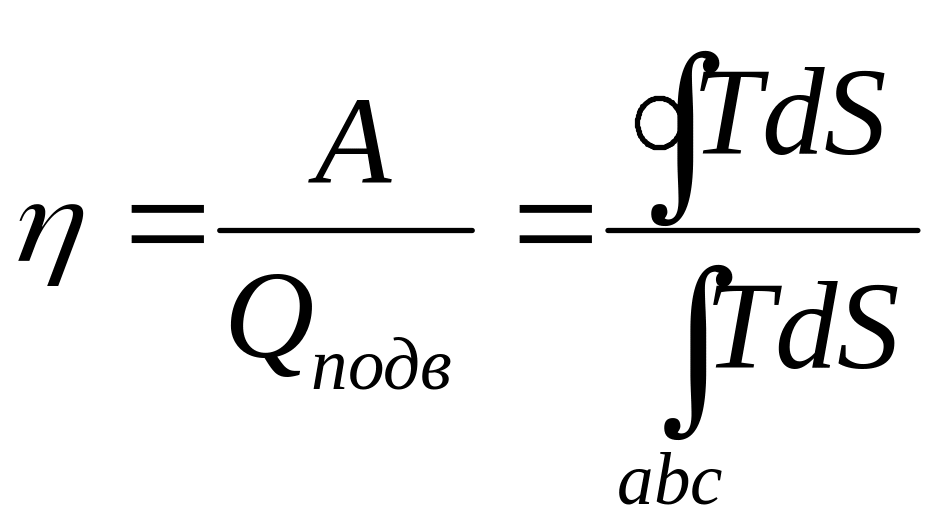
3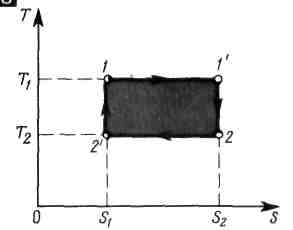 ) Прямой цикл Карно независимо от природы рабочего тела изображается в Т — S-диаграмме в виде прямоугольника, стороны которого параллельны осям координат

Термический КПД цикла Карно не зависит от природы рабочего тела и определяется только температурами нагревателя и холодильника

Таким образом мы доказали важное положение термодинамики, называемое теоремой Карно:

Теорема Карно и формула служат основанием для установления термодинамической шкалы температур:

Таким образом, для сравнения температур Т₁ и Т₂ двух тел нужно осуществить обратимый цикл Карно, в котором эти тела являются нагревателем и холодильником. Отношение температур тел равно отношению абсолютных значений количеств теплоты, отданных или полученных телами в этом цикле. По теореме Карно, химический состав рабочего тела, осуществляющего цикл, не влияет на результаты сравнения температур. Поэтому установленная таким образом термодинамическая шкала температур не связана со свойствами какого-либо определенного термометрического тела. В этом состоит большое достоинство такой шкалы.

Однако вследствие необратимости реальных термодинамических процессов такой способ сравнения температур практически неосуществим и имеет лишь принципиальное значение.